Intermediate Microeconomics and Its Application 12th Edition by Walter Nicholson,Christopher Snyder

Exercise 2

The following game is a version of the Prisoners' Dilemma, but the payoffs are slightly different than in Table 5.1.
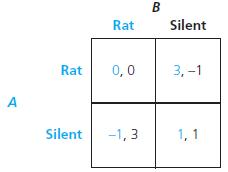
a. Verify that the Nash equilibrium is the usual one for the Prisoners' Dilemma and that both players have dominant strategies.
b. Suppose the stage game is played an indefinite number of times with a probability g the game is continued to the next stage and 1 - g that the game ends for good. Compute the level of g that is required for a subgame-perfect equilibrium in which both players play a trigger strategy where both are Silent if no one deviates but resort to a grim strategy (that is, both play Rat forever after) if anyone deviates to Rat.
c. Continue to suppose the stage game is played an indefinite number of times, as in b. Is there a value of g for which there exists a subgame-perfect equilibrium in which both players play a trigger strategy where both are Silent if no one deviates but resort to tit-for-tat (that is, both play Rat for one period and go back to Silent forever after that) if anyone deviates to Rat? Remember that g is a probability, so it must be between 0 and 1.