
Intermediate Microeconomics and Its Application 12th Edition by Walter Nicholson,Christopher Snyder
Edition 12ISBN: 978-1133189022
Intermediate Microeconomics and Its Application 12th Edition by Walter Nicholson,Christopher Snyder
Edition 12ISBN: 978-1133189022 Exercise 3
Answer question 5 using two specific production functions as examples:
a. A fixed-proportions production function
b. A Cobb-Douglas production function of the form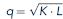
(See Problems for a discussion of this case.)Suppose that the hourly output of chili at a barbecue (q, measured in pounds) is characterized by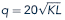
where K is the number of large pots used each hour and L is the number of worker hours employed.
a. Graph the q = 2,000 pounds per hour isoquant.
b. The point K = 100, L = 100 is one point on the q = 2,000 isoquant. What value of K corresponds to L = 101 on that isoquant? What is the approximate value for the RTS at K = 100, L = 100?
c. The point K = 25, L = 400 also lies on the q = 2,000 isoquant. If L = 401, what must K be for this input combination to lie on the q = 2,000 isoquant? What is the approximate value of the RTS at K = 25, L = 400?
d. For this production function, the RTS is
RTS = K/L
Compare the results from applying this formula to those you calculated in part b and part c. To convince yourself further, perform a similar calculation for the point K = 200, L = 50.
e. If technical progress shifted the production function to
all of the input combinations identified earlier can now produce q = 4,000 pounds per hour. Would the various values calculated for the RTS be changed as a result of this technical progress, assuming now that the RTS is measured along the q = 4,000 isoquant?
The production function
q = K a L b
where 0 ? a, b ? 1 is called a Cobb-Douglas production function. This function is widely used in economic research. Using the function, show the following:
a. The production function in Equation is a special case of the Cobb-Douglas.
b. If a + b = 1, a doubling of K and L will double q.
c. If a + b 1, a doubling of K and L will less than double q.
d. If a + b 1, a doubling of K and L will more than double q.
e. Using the results from part b through part d, what can you say about the returns to scale exhibited by the Cobb-Douglas function?
For the Cobb-Douglas production function in Problem it can be shown (using calculus) that
MP K = aK a-1 L b
MP L = bK a L b-1
If the Cobb-Douglas exhibits constant returns to scale (a + b = 1), show that
a. Both marginal productivities are diminishing.
b. The RTS for this function is given by
c. The function exhibits a diminishing RTS.
Equation
a. A fixed-proportions production function
b. A Cobb-Douglas production function of the form
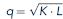
(See Problems for a discussion of this case.)Suppose that the hourly output of chili at a barbecue (q, measured in pounds) is characterized by
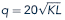
where K is the number of large pots used each hour and L is the number of worker hours employed.
a. Graph the q = 2,000 pounds per hour isoquant.
b. The point K = 100, L = 100 is one point on the q = 2,000 isoquant. What value of K corresponds to L = 101 on that isoquant? What is the approximate value for the RTS at K = 100, L = 100?
c. The point K = 25, L = 400 also lies on the q = 2,000 isoquant. If L = 401, what must K be for this input combination to lie on the q = 2,000 isoquant? What is the approximate value of the RTS at K = 25, L = 400?
d. For this production function, the RTS is
RTS = K/L
Compare the results from applying this formula to those you calculated in part b and part c. To convince yourself further, perform a similar calculation for the point K = 200, L = 50.
e. If technical progress shifted the production function to

all of the input combinations identified earlier can now produce q = 4,000 pounds per hour. Would the various values calculated for the RTS be changed as a result of this technical progress, assuming now that the RTS is measured along the q = 4,000 isoquant?
The production function
q = K a L b
where 0 ? a, b ? 1 is called a Cobb-Douglas production function. This function is widely used in economic research. Using the function, show the following:
a. The production function in Equation is a special case of the Cobb-Douglas.
b. If a + b = 1, a doubling of K and L will double q.
c. If a + b 1, a doubling of K and L will less than double q.
d. If a + b 1, a doubling of K and L will more than double q.
e. Using the results from part b through part d, what can you say about the returns to scale exhibited by the Cobb-Douglas function?
For the Cobb-Douglas production function in Problem it can be shown (using calculus) that
MP K = aK a-1 L b
MP L = bK a L b-1
If the Cobb-Douglas exhibits constant returns to scale (a + b = 1), show that
a. Both marginal productivities are diminishing.
b. The RTS for this function is given by

c. The function exhibits a diminishing RTS.
Equation

Explanation
a) Assume a fixed proportions production...
Intermediate Microeconomics and Its Application 12th Edition by Walter Nicholson,Christopher Snyder
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255



