Intermediate Microeconomics and Its Application 12th Edition by Walter Nicholson,Christopher Snyder

Exercise 5

Returning to the gumball producer in Problem 7.2, let's look at the possibility that producing these delectable treats does not necessarily experience constant returns to scale.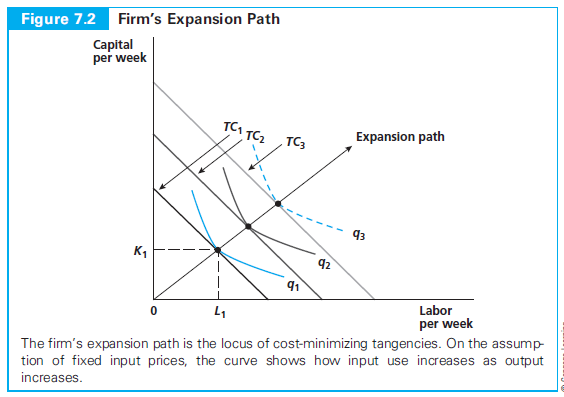
a. In Problem 7.2, we showed that the cost function for gumballs was given by TC =q (2v + w), where q is output of gumballs (in thousands), v is the rental rate for gumball presses, and w is the hourly wage. What sort of returns to scale did the underlying production function have? Does the cost function show economies or diseconomies of scale?
b. Suppose instead that the gumball cost function is given by . Does this function show economies or diseconomies of scale? What does the graph of the total cost curve for this function look like? What do the implies average and marginal cost curves look like?
c. Suppose now that the gumball cost function is TC = (2v + w)q 2. Does this function show economies or diseconomies of scale? Illustrate this by graphing the total, average, and marginal cost curves for this function.
d. Economists sometimes measure the degree of economies of scale by S = AC/MC. This measure makes sense: if S 1, then AC MC, implying AC slopes up (because MC pulls it up), in which case we have diseconomies of scale. On the other hand, if S 1, then AC MC, implying AC slopes down (because MC pulls it down) and we have (positive) economies of scale. Suppose that the gumball production has associated total and marginal cost functions TC = (2v + w)q a and MC = a(2v + w)q a?1. Compute S in this case, and show how it relates to a. Discuss how the presence of economies or diseconomies of scale relates to a.