Intermediate Microeconomics and Its Application 12th Edition by Walter Nicholson,Christopher Snyder

Exercise 4

The Edgeworth box diagram can also be used to show how a production possibility frontier is constructed for an economy as a whole. Suppose there are only two goods that might be produced (X and Y), each using two inputs, capital (K) and labor (L). In order to construct the X-Y production possibility frontier, we must look for efficient allocations of the total capital and labor available.
a. Draw an Edgeworth box with dimensions given by the total quantities of capital and labor available (see Figure).
b. Consider the lower-left corner of the box to be the origin for the isoquant map for good X. Draw a few of the X isoquants.
c. Now consider the upper-right corner of the box to be the origin for the isoquant map for good Y. Draw a few Y isoquants (as in Figure) in the Edgeworth box.
d. What are the efficient points in the box you have drawn? What condition must hold for a given allocation of K and L to be efficient?
e. The production possibility frontier for X and Y consists of all the efficient allocations in the Edgeworth box. Explain why this is so. Also explain why inefficient points in the box would be z'rasz'de the production possibility frontier.
f. Use the connection between your box diagram and the production possibility frontier to discuss what the frontier would look like in the following cases:
i. Production of good X uses only labor, production of good Y uses only capital.
ii. Both X and Y are produced using K and L in the same fixed proportions as the inputs are available in the economy and both exhibit constant returns to scale.
iii. Both X and Y have the same production function and both exhibit constant returns to scale.
iv. Both X and Y are produced using the same production function and both exhibit increasing returns to scale.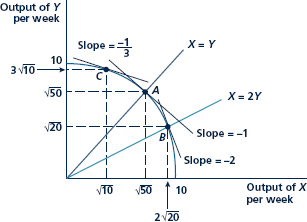
Here, the production possibility frontier is given by X2 þ Y2 ¼ 100. If preferences require X ¼ Y, point A will be efficient and PX/PY ¼ 1. If preferences require X ¼ 2Y, point B will be efficient, PX/PY ¼ 2. If preferences require PX/PY ¼ 1=3, point C is efficient.
The Edgeworth box diagram permits all possible allocations of two goods (X and Y ) to be visualized. If we consider the corner OS to be Smith's ''origin'' and OJ to be Jones's, then the allocation represented by point E would have Smith getting XE S and YE S , and Jones would receive what is left over (XE J , YE J ). One purpose of this diagram is to discover which of the possible locations within the box can be reached through voluntary exchange.