Chat with AI
Intermediate Microeconomics and Its Application 12th Edition by Walter Nicholson,Christopher Snyder
Edition 12ISBN: 978-1133189022Intermediate Microeconomics and Its Application 12th Edition by Walter Nicholson,Christopher Snyder
Edition 12ISBN: 978-1133189022 Exercise 32
Continuous Compounding
Perhaps surprisingly, the mathematics involved with "continuous" compounding (that is, compounding that occurs every instant of time) is really quite simple. A familiarity with continuous compounding can allow you to make very good approximations to interest calculations that would otherwise be very cumbersome.
The Amazing e
One of the most important constants1 in mathematics is the number "e," which takes a value of approximately 2.718281828. The mathematician Euler discovered the constant in 1727, thereby explaining why this letter was chosen. The constant seems to turn up everywhere in mathematics. For us, the most important property of e is that it is used in continuous compounding. Consider an annual interest rate of i that will be compounded n times in one year. The result of this compounding will be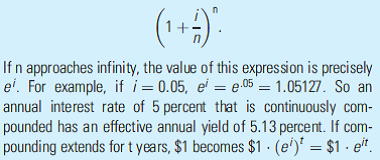
The Rule of 70
A simple application of continuous compounding is to provide a rule of thumb for calculating doubling time for any given interest rate. To find the time anything doubles we wish to solve the equation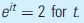
Taking natural logarithms yields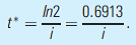 
If we approximate 0:6913 as 0.7, this is the "rule of 70." To find any doubling time, just divide the interest rate into 0.70. For example, anything growing at 5 percent per year will double in about 14 (= 0.7/0.05) years.
Growth Rates of Products and Ratios
When economic magnitudes follow exponential growth rates, calculations combining two or more series can be especially simple. For example, suppose we have two series, x and y growing at rates of r 1 and r 2 respectively. Then the product x · y is growing like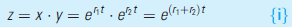
That is, the product of the two variables is growing at a rate that equals the sum of the individual growth rates. If, for example, real GDP is growing at 3 percent per year and inflation is 2 percent per year, nominal GDP is growing at 5 percent per year. A similar result works for growth rates in the ratio of two variables. That is, the ratio of two variables grows at a rate that equals the difference in their growth rates. For example, if real GDP is growing at 3 percent per year and population growth is 1 percent per year, per capita GDP is growing at 2 percent per year.
Discounting
With continuous compounding, the appropriate discount factor is e?it , which plays the same role that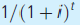
does in discrete discounting. Any continuous stream of payments can be discounted to the present day by using this factor. As a simple example, the value of payments of $1 per year for 25 years discounted at an interest rate of 5 percent is given by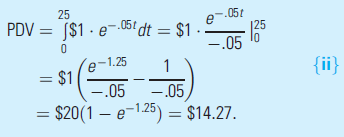 
The U.S. consumer price index was 152 in 1995 and 233 in 2013. How would you use continuous compounding formulas to calculate the annual rate of change during this 18-year period?
Perhaps surprisingly, the mathematics involved with "continuous" compounding (that is, compounding that occurs every instant of time) is really quite simple. A familiarity with continuous compounding can allow you to make very good approximations to interest calculations that would otherwise be very cumbersome.
The Amazing e
One of the most important constants1 in mathematics is the number "e," which takes a value of approximately 2.718281828. The mathematician Euler discovered the constant in 1727, thereby explaining why this letter was chosen. The constant seems to turn up everywhere in mathematics. For us, the most important property of e is that it is used in continuous compounding. Consider an annual interest rate of i that will be compounded n times in one year. The result of this compounding will be
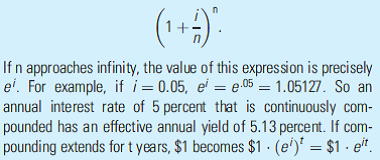
The Rule of 70
A simple application of continuous compounding is to provide a rule of thumb for calculating doubling time for any given interest rate. To find the time anything doubles we wish to solve the equation
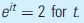Taking natural logarithms yields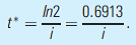 If we approximate 0:6913 as 0.7, this is the "rule of 70." To find any doubling time, just divide the interest rate into 0.70. For example, anything growing at 5 percent per year will double in about 14 (= 0.7/0.05) years.
Growth Rates of Products and Ratios
When economic magnitudes follow exponential growth rates, calculations combining two or more series can be especially simple. For example, suppose we have two series, x and y growing at rates of r 1 and r 2 respectively. Then the product x · y is growing like
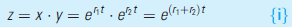
That is, the product of the two variables is growing at a rate that equals the sum of the individual growth rates. If, for example, real GDP is growing at 3 percent per year and inflation is 2 percent per year, nominal GDP is growing at 5 percent per year. A similar result works for growth rates in the ratio of two variables. That is, the ratio of two variables grows at a rate that equals the difference in their growth rates. For example, if real GDP is growing at 3 percent per year and population growth is 1 percent per year, per capita GDP is growing at 2 percent per year.
Discounting
With continuous compounding, the appropriate discount factor is e?it , which plays the same role that
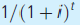does in discrete discounting. Any continuous stream of payments can be discounted to the present day by using this factor. As a simple example, the value of payments of $1 per year for 25 years discounted at an interest rate of 5 percent is given by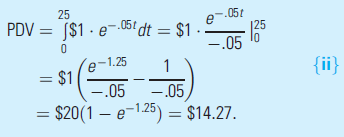 The U.S. consumer price index was 152 in 1995 and 233 in 2013. How would you use continuous compounding formulas to calculate the annual rate of change during this 18-year period?
Explanation
Verified
Verified
To calculate the continuous compounding ...
Intermediate Microeconomics and Its Application 12th Edition by Walter Nicholson,Christopher Snyder
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255
