
Microeconomics 2nd Edition by Douglas Bernheim
Edition 2ISBN: 978-0071287616
Microeconomics 2nd Edition by Douglas Bernheim
Edition 2ISBN: 978-0071287616 Exercise 2
Calculus Problem 1, but assume that David has the following preferences. Before he leaves, he would like to choose his spending to maximize the utility function
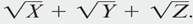 But on the first day of his trip, he would like to choose his spending to maximize the utility function
But on the first day of his trip, he would like to choose his spending to maximize the utility function
 , and on the second day he would like to choose his remaining spending to maximize the utility function
, and on the second day he would like to choose his remaining spending to maximize the utility function
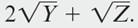
Calculus Problem 1
David is leaving on a three-day business trip. He has a meal allowance of $60. Let's use X to stand for the amount he spends on food the first day, Y for the amount he spends the second day, and Z for the amount he spends on the third day; David's budget constraint is X + Y + Z = 60. Before he leaves, he would like to choose his spending to maximize the utility function ln( X ) + ln( Y ) + ln( Z ), where ln stands for the natural logarithm. But on the first day of his trip, he would like to choose his spending to maximize the utility function 2ln( X ) + ln( Y ) + ln( Z ), and on the second day he would like to choose his remaining spending to maximize the utility function 2ln( Y ) 1 ln(Z). If he could commit to a plan before leaving, how would he spend his money If he could commit to a plan on the first day of his trip, how would he spend his money Assuming he cannot commit to a plan, and that he correctly anticipates his decisions on subsequent days, how will he actually spend his money Is he dynamically consistent Why or why not
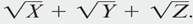 But on the first day of his trip, he would like to choose his spending to maximize the utility function
But on the first day of his trip, he would like to choose his spending to maximize the utility function  , and on the second day he would like to choose his remaining spending to maximize the utility function
, and on the second day he would like to choose his remaining spending to maximize the utility function 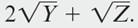
Calculus Problem 1
David is leaving on a three-day business trip. He has a meal allowance of $60. Let's use X to stand for the amount he spends on food the first day, Y for the amount he spends the second day, and Z for the amount he spends on the third day; David's budget constraint is X + Y + Z = 60. Before he leaves, he would like to choose his spending to maximize the utility function ln( X ) + ln( Y ) + ln( Z ), where ln stands for the natural logarithm. But on the first day of his trip, he would like to choose his spending to maximize the utility function 2ln( X ) + ln( Y ) + ln( Z ), and on the second day he would like to choose his remaining spending to maximize the utility function 2ln( Y ) 1 ln(Z). If he could commit to a plan before leaving, how would he spend his money If he could commit to a plan on the first day of his trip, how would he spend his money Assuming he cannot commit to a plan, and that he correctly anticipates his decisions on subsequent days, how will he actually spend his money Is he dynamically consistent Why or why not
Explanation
The behavioral economics study the psych...
Microeconomics 2nd Edition by Douglas Bernheim
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255



