Chat with AI
Essentials of Economics 8th Edition by Bradley Schiller
Edition 8ISBN: 978-0073511399Essentials of Economics 8th Edition by Bradley Schiller
Edition 8ISBN: 978-0073511399 Exercise 2
Suppose in problem 3 that a second worker became available. Illustrate the resulting change in production possibilities. Now what would be the opportunity cost of sanding two floors?
Explanation
Verified
Verified
If another worker becomes available, then the total labor time available is 48 labor hours. It takes four hours of labor time to paint a room. Therefore with 48 labor hours available the number of rooms that could be painted if the entire time is invested in painting rooms is equal to:
(rooms)
An alternative way of going about this is realizing that if one worker can paint 6 rooms iN2 4 hours, theN2 workers can paint 12 rooms in the same time.
Again if the 48 hours are invested in sanding floors instead, the number of floors that can be sanded are:
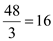(floors)
(Or alternatively, 2 workers can sand the double number of rooms that 1 worker can and therefore, the total number of rooms that can be sanded by 2 workers is 8.)
This is shown in the production possibilities curve below;
Production Possibilities Curve:
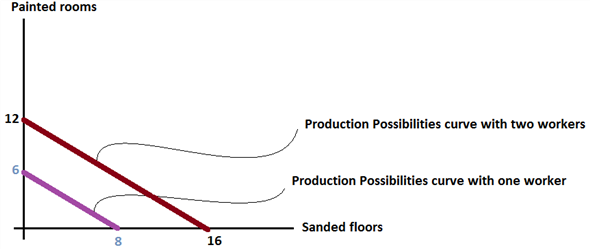In the diagram above the production possibilities curve with two workers available is shown along with the previous production possibilities curve (with only one worker available).
One worker can paint one room in four hours. Thus, two workers paint one room in two hours. Again, it takes one worker three hours to sand a floor. Therefore, It takes two workerS1 .5 hours to sand a floor. And thus, two floors can be sanded by two workers together in 3 hours. Therefore the opportunity cost of sanding these two floors is the number of rooms that could be painted by two workers in three hours. Thus, the opportunity cost is:
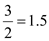rooms.
(rooms)An alternative way of going about this is realizing that if one worker can paint 6 rooms iN2 4 hours, theN2 workers can paint 12 rooms in the same time.
Again if the 48 hours are invested in sanding floors instead, the number of floors that can be sanded are:
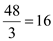(floors)(Or alternatively, 2 workers can sand the double number of rooms that 1 worker can and therefore, the total number of rooms that can be sanded by 2 workers is 8.)
This is shown in the production possibilities curve below;
Production Possibilities Curve:
In the diagram above the production possibilities curve with two workers available is shown along with the previous production possibilities curve (with only one worker available). One worker can paint one room in four hours. Thus, two workers paint one room in two hours. Again, it takes one worker three hours to sand a floor. Therefore, It takes two workerS1 .5 hours to sand a floor. And thus, two floors can be sanded by two workers together in 3 hours. Therefore the opportunity cost of sanding these two floors is the number of rooms that could be painted by two workers in three hours. Thus, the opportunity cost is:
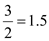rooms.
Essentials of Economics 8th Edition by Bradley Schiller
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255
