
Introduction to Econometrics 3rd Edition by James Stock, Mark Watson
Edition 3ISBN: 978-9352863501
Introduction to Econometrics 3rd Edition by James Stock, Mark Watson
Edition 3ISBN: 978-9352863501 Exercise 31
Suppose Y i ,i = 1,2,..., n, are i.i.d. random variables, each distributed N (10,4).
a. Compute Pr(9.6
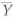 10.4) when (i) n = 20, (ii) n = 100, and (iii) n = 1,000.
10.4) when (i) n = 20, (ii) n = 100, and (iii) n = 1,000.
b. Suppose c is a positive number. Show that Pr(10 - c
 10 + c) becomes close to 1.0 as n grows large.
10 + c) becomes close to 1.0 as n grows large.
c. Use your answer in (b) to argue that
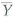 converges in probability to 10.
converges in probability to 10.
a. Compute Pr(9.6
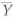 10.4) when (i) n = 20, (ii) n = 100, and (iii) n = 1,000.
10.4) when (i) n = 20, (ii) n = 100, and (iii) n = 1,000.b. Suppose c is a positive number. Show that Pr(10 - c
 10 + c) becomes close to 1.0 as n grows large.
10 + c) becomes close to 1.0 as n grows large.c. Use your answer in (b) to argue that
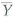 converges in probability to 10.
converges in probability to 10.Explanation
Random variables refers to the value of ...
Introduction to Econometrics 3rd Edition by James Stock, Mark Watson
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255



