
Introduction to Econometrics 3rd Edition by James Stock, Mark Watson
Edition 3ISBN: 978-9352863501
Introduction to Econometrics 3rd Edition by James Stock, Mark Watson
Edition 3ISBN: 978-9352863501 Exercise 23
X and Z are two jointly distributed random variables. Suppose you know the value of Z , but not the value of X. Let
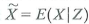 denote a guess of the value of X using the information on Z , and let
denote a guess of the value of X using the information on Z , and let
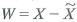 denote the error associated with this guess.
denote the error associated with this guess.
a. Show that E ( W ) = 0.
b. Show that E ( WZ ) = 0.
c. Let
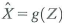 denote another guess of X using Z, and
denote another guess of X using Z, and
 denote its error. Show that
denote its error. Show that
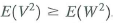 .
.
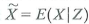 denote a guess of the value of X using the information on Z , and let
denote a guess of the value of X using the information on Z , and let 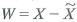 denote the error associated with this guess.
denote the error associated with this guess.a. Show that E ( W ) = 0.
b. Show that E ( WZ ) = 0.
c. Let
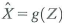 denote another guess of X using Z, and
denote another guess of X using Z, and  denote its error. Show that
denote its error. Show that 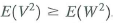 .
.Explanation
It is told that:
•
and
are two joi...
Introduction to Econometrics 3rd Edition by James Stock, Mark Watson
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255



