
Introduction to Econometrics 3rd Edition by James Stock, Mark Watson
Edition 3ISBN: 978-9352863501
Introduction to Econometrics 3rd Edition by James Stock, Mark Watson
Edition 3ISBN: 978-9352863501 Exercise 25
Let Ybe a Bernoulli random variable with success probability Pr(Y = 1) = p, and,let Y 1 , …, Y n be i.i.d. draws from this distribution. Let
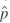 be the fraction of successes (Is) in this sample.
be the fraction of successes (Is) in this sample.
a. Show that
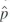 = Y.
= Y.
b. Show that
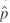 is an unbiased estimator of p.
is an unbiased estimator of p.
c. Show that var(
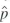 ) =p(l - p)/n.
) =p(l - p)/n.
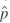 be the fraction of successes (Is) in this sample.
be the fraction of successes (Is) in this sample.a. Show that
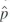 = Y.
= Y. b. Show that
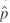 is an unbiased estimator of p.
is an unbiased estimator of p. c. Show that var(
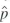 ) =p(l - p)/n.
) =p(l - p)/n.Explanation
We are told that:
-
is a Bernoulli ra...
Introduction to Econometrics 3rd Edition by James Stock, Mark Watson
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255



