
Introduction to Econometrics 3rd Edition by James Stock, Mark Watson
Edition 3ISBN: 978-9352863501
Introduction to Econometrics 3rd Edition by James Stock, Mark Watson
Edition 3ISBN: 978-9352863501 Exercise 4
Let Y a and Y b denote Bernoulli random variables from two different populations, denoted a and b. Suppose that E(Y a ) = p a and E(Y b ) = p b. A random sample of size n a is chosen from population a, with sample average denoted
 a , and a random sample of size n b is chosen from population b , with sample average denoted
a , and a random sample of size n b is chosen from population b , with sample average denoted
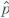 b. Suppose the sample from population a is independent of the sample from population b.
b. Suppose the sample from population a is independent of the sample from population b.
a. Show that E(
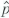 a ) = p a and var(
a ) = p a and var(
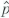 a ) = p a (1 - p a ) /n a. Show that E (
a ) = p a (1 - p a ) /n a. Show that E (
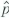 b ) =Pb and var (
b ) =Pb and var (
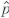 b ) =p b (1 -p b ) /n b.
b ) =p b (1 -p b ) /n b.
b. Show that var

c. Suppose that n a and n b are large. Show that a 95% confidence interval for Pa - Pb is given by
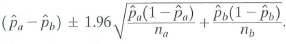
How would you construct a 90% confidence interval for p a - p b
d. Read the box "A Novel Way to Boost Retirement Savings" in Section 3.5. Let population a denote the "opt-out" (treatment) group and population b denote the "opt-in" (control) group. Construct a 95% confidence interval for the treatment effect, p a - p b.
 a , and a random sample of size n b is chosen from population b , with sample average denoted
a , and a random sample of size n b is chosen from population b , with sample average denoted 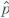 b. Suppose the sample from population a is independent of the sample from population b.
b. Suppose the sample from population a is independent of the sample from population b. a. Show that E(
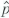 a ) = p a and var(
a ) = p a and var( 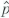 a ) = p a (1 - p a ) /n a. Show that E (
a ) = p a (1 - p a ) /n a. Show that E ( 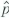 b ) =Pb and var (
b ) =Pb and var ( 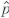 b ) =p b (1 -p b ) /n b.
b ) =p b (1 -p b ) /n b. b. Show that var

c. Suppose that n a and n b are large. Show that a 95% confidence interval for Pa - Pb is given by
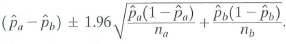
How would you construct a 90% confidence interval for p a - p b
d. Read the box "A Novel Way to Boost Retirement Savings" in Section 3.5. Let population a denote the "opt-out" (treatment) group and population b denote the "opt-in" (control) group. Construct a 95% confidence interval for the treatment effect, p a - p b.
Explanation
We are told that:
-
and
are Bernou...
Introduction to Econometrics 3rd Edition by James Stock, Mark Watson
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255



