
Introduction to Econometrics 3rd Edition by James Stock, Mark Watson
Edition 3ISBN: 978-9352863501
Introduction to Econometrics 3rd Edition by James Stock, Mark Watson
Edition 3ISBN: 978-9352863501 Exercise 4
(Requires calculus) Consider the regression model
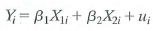
for i = 1,..., n. (Notice that there is no constant term in the regression.) Following analysis like that used in Appendix 4.2:
a. Specify the least squares function that is minimized by OLS.
b. Compute the partial derivatives of the objective function with respect to b 1 and b 2.
c. Suppose
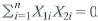 . Show that
. Show that
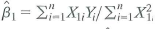 .
.
d. Suppose
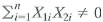 . Derive an expression for ß 1 as a function of the data ( Y i X 1i X 2i ) , i = 1,..., n.
. Derive an expression for ß 1 as a function of the data ( Y i X 1i X 2i ) , i = 1,..., n.
e. Suppose that the model includes an intercept:
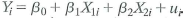 . Show that the least squares estimators satisfy
. Show that the least squares estimators satisfy
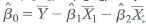 .
.
f. As in (e), suppose that the model contains an intercept. Also suppose that
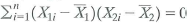 . Show that
. Show that
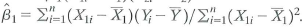 . How does this compare to the OLS estimator of ß x from the regression that omits X 2
. How does this compare to the OLS estimator of ß x from the regression that omits X 2
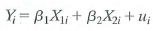
for i = 1,..., n. (Notice that there is no constant term in the regression.) Following analysis like that used in Appendix 4.2:
a. Specify the least squares function that is minimized by OLS.
b. Compute the partial derivatives of the objective function with respect to b 1 and b 2.
c. Suppose
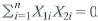 . Show that
. Show that 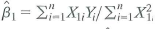 .
. d. Suppose
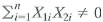 . Derive an expression for ß 1 as a function of the data ( Y i X 1i X 2i ) , i = 1,..., n.
. Derive an expression for ß 1 as a function of the data ( Y i X 1i X 2i ) , i = 1,..., n. e. Suppose that the model includes an intercept:
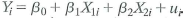 . Show that the least squares estimators satisfy
. Show that the least squares estimators satisfy 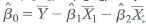 .
. f. As in (e), suppose that the model contains an intercept. Also suppose that
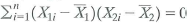 . Show that
. Show that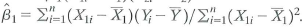 . How does this compare to the OLS estimator of ß x from the regression that omits X 2
. How does this compare to the OLS estimator of ß x from the regression that omits X 2Explanation
Given the regression model:
a) We need...
Introduction to Econometrics 3rd Edition by James Stock, Mark Watson
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255



