
Introduction to Econometrics 3rd Edition by James Stock, Mark Watson
Edition 3ISBN: 978-9352863501
Introduction to Econometrics 3rd Edition by James Stock, Mark Watson
Edition 3ISBN: 978-9352863501 Exercise 6
Consider TSLS estimation with a single included endogenous variable and a single instrument. Then the predicted value from the first-stage regression is
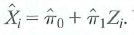 Use the definition of the sample variance and covariance to show that
Use the definition of the sample variance and covariance to show that
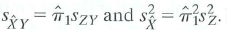 Use this result to fill in the steps of the derivation in Appendix of Equation (12.4).
Use this result to fill in the steps of the derivation in Appendix of Equation (12.4).
Appendix
Derivation of the Formula for the TSLS Estimator in Equation (12.4)
The first stage of TSLS is to regress X i on the instrument Z i by OLS and then compute the OLS predicted value
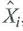 , and the second stage is to regress Y i on
, and the second stage is to regress Y i on
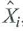 by OLS. Accordingly, the formula for the TSLS estimator, expressed in terms of the predicted value
by OLS. Accordingly, the formula for the TSLS estimator, expressed in terms of the predicted value
 is the formula for the OLS estimator in Key Concept 4.2, with
is the formula for the OLS estimator in Key Concept 4.2, with
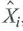 replacing X i. That is,
replacing X i. That is,
 , where
, where
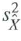 , is the sample variance of
, is the sample variance of
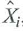 and
and
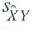 is the sample covariance between Y i and
is the sample covariance between Y i and
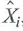
Because X i is the predicted value of X i from the first-stage regression,
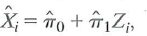 , the definitions of sample variances and covariances imply that
, the definitions of sample variances and covariances imply that
 (Exercise 12.4). Thus, the TSLS estimator can be written as
(Exercise 12.4). Thus, the TSLS estimator can be written as
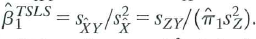 . Finally,
. Finally,
 is the OLS slope coefficient from the first stage of TSLS, so
is the OLS slope coefficient from the first stage of TSLS, so
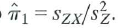 Substitution of this formula for
Substitution of this formula for
 into the formula
into the formula
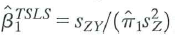 yields the formula for the TSLS estimator in Equation (12.4).
yields the formula for the TSLS estimator in Equation (12.4).
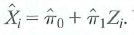 Use the definition of the sample variance and covariance to show that
Use the definition of the sample variance and covariance to show that 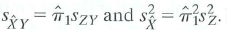 Use this result to fill in the steps of the derivation in Appendix of Equation (12.4).
Use this result to fill in the steps of the derivation in Appendix of Equation (12.4).Appendix
Derivation of the Formula for the TSLS Estimator in Equation (12.4)
The first stage of TSLS is to regress X i on the instrument Z i by OLS and then compute the OLS predicted value
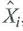 , and the second stage is to regress Y i on
, and the second stage is to regress Y i on 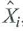 by OLS. Accordingly, the formula for the TSLS estimator, expressed in terms of the predicted value
by OLS. Accordingly, the formula for the TSLS estimator, expressed in terms of the predicted value  is the formula for the OLS estimator in Key Concept 4.2, with
is the formula for the OLS estimator in Key Concept 4.2, with 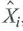 replacing X i. That is,
replacing X i. That is,  , where
, where 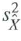 , is the sample variance of
, is the sample variance of 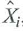 and
and 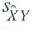 is the sample covariance between Y i and
is the sample covariance between Y i and 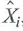
Because X i is the predicted value of X i from the first-stage regression,
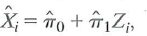 , the definitions of sample variances and covariances imply that
, the definitions of sample variances and covariances imply that (Exercise 12.4). Thus, the TSLS estimator can be written as
(Exercise 12.4). Thus, the TSLS estimator can be written as 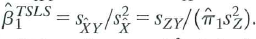 . Finally,
. Finally,  is the OLS slope coefficient from the first stage of TSLS, so
is the OLS slope coefficient from the first stage of TSLS, so 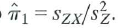 Substitution of this formula for
Substitution of this formula for  into the formula
into the formula 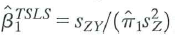 yields the formula for the TSLS estimator in Equation (12.4).
yields the formula for the TSLS estimator in Equation (12.4).Explanation
For a TSLS regression, we have:
Here, ...
Introduction to Econometrics 3rd Edition by James Stock, Mark Watson
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255



