
Introduction to Econometrics 3rd Edition by James Stock, Mark Watson
Edition 3ISBN: 978-9352863501
Introduction to Econometrics 3rd Edition by James Stock, Mark Watson
Edition 3ISBN: 978-9352863501 Exercise 9
Prove the following results about conditional means, forecasts, and forecast errors:
a. Let W be a random variable with mean and variance and let c be a constant. Show that
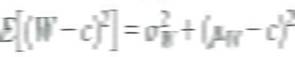
b. Consider the problem of forecasting Y t using data on Y t-1 , Y t-2 , …, Let f t-1 denote some forecast of Y t , where the subscript t - 1 on f t-1 indicates that the forecast is a function of data through date t- 1. Let be the conditional mean squared error of the forecast conditional on Y observed through date t - 1. Show that the conditional mean squared forecast error is minimized when
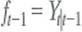 , where
, where
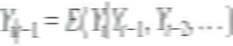
c. Let u t denote the error in Equation (14.14). Show that cov ( u t u t-j ) = 0 for; j 0.
a. Let W be a random variable with mean and variance and let c be a constant. Show that
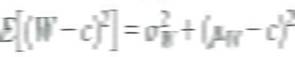
b. Consider the problem of forecasting Y t using data on Y t-1 , Y t-2 , …, Let f t-1 denote some forecast of Y t , where the subscript t - 1 on f t-1 indicates that the forecast is a function of data through date t- 1. Let be the conditional mean squared error of the forecast conditional on Y observed through date t - 1. Show that the conditional mean squared forecast error is minimized when
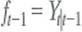 , where
, where 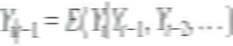
c. Let u t denote the error in Equation (14.14). Show that cov ( u t u t-j ) = 0 for; j 0.
Explanation
The random variable W is distributed wit...
Introduction to Econometrics 3rd Edition by James Stock, Mark Watson
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255



