
Introduction to Econometrics 3rd Edition by James Stock, Mark Watson
Edition 3ISBN: 978-9352863501
Introduction to Econometrics 3rd Edition by James Stock, Mark Watson
Edition 3ISBN: 978-9352863501 Exercise 11
Consider the regression model Y t = 0 + 1 X t + u t where u, follows the stationary AR(1) mode with
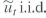 . with mean 0 and variance and |
. with mean 0 and variance and |
1 | 1, the regressor X t follows the stationary AR(1) mode with e t i.i.d. with mean 0 and variance and | 1 | 1, and e t is independent of for all t and i.
a. Show that var and var( X t ) =
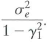 .
.
b. Show that cov and cov
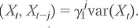 .
.
c. Show that corr and corr
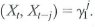 .
.
d. Consider the terms and f T in Equation (15.14).
i. Show that where is the variance of X and
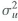 , is the variance of u.
, is the variance of u.
ii. Derive an expression for f
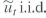 . with mean 0 and variance and |
. with mean 0 and variance and |1 | 1, the regressor X t follows the stationary AR(1) mode with e t i.i.d. with mean 0 and variance and | 1 | 1, and e t is independent of for all t and i.
a. Show that var and var( X t ) =
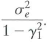 .
.b. Show that cov and cov
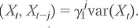 .
.c. Show that corr and corr
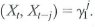 .
.d. Consider the terms and f T in Equation (15.14).
i. Show that where is the variance of X and
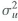 , is the variance of u.
, is the variance of u. ii. Derive an expression for f
Explanation
b) The u term can be defined recursively...
Introduction to Econometrics 3rd Edition by James Stock, Mark Watson
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255



