Chat with AI
Introduction to Econometrics 3rd Edition by James Stock, Mark Watson
Edition 3ISBN: 978-9352863501Introduction to Econometrics 3rd Edition by James Stock, Mark Watson
Edition 3ISBN: 978-9352863501 Exercise 10
Let W be an m × 1 vector with covariance matrix
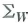where
is finite and positive definite. Let c be a nonrandom m × 1 vector, and let
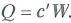
a. Show that var
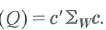
b. Suppose that c 0 m Show that 0 var(Q) .
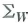where is finite and positive definite. Let c be a nonrandom m × 1 vector, and let 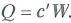a. Show that var
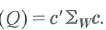
b. Suppose that c 0 m Show that 0 var(Q) .
Explanation
Verified
Verified
a) The variable Q is defined as
Here c...
Introduction to Econometrics 3rd Edition by James Stock, Mark Watson
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255
