
Introduction to Econometrics 3rd Edition by James Stock, Mark Watson
Edition 3ISBN: 978-9352863501
Introduction to Econometrics 3rd Edition by James Stock, Mark Watson
Edition 3ISBN: 978-9352863501 Exercise 5
Consider the problem of minimizing the sum of squared residuals subject to the constraint that Rb = r, where R is q × ( k + 1) with rank cj. Let
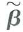 be the value of b that solves the constrained minimization problem.
be the value of b that solves the constrained minimization problem.
a. Show that the Lagrangian for the minimization problem is L(b , ) = ( Y- Xb ) ' ( Y-Xb ) + ' ( Rb - r ), where is a q × 1 vector of Lagrange multipliers.
b. Show that
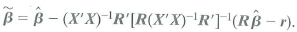
c. Show that
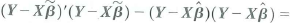
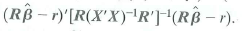
d. Show that F in Equation (18.36) is equivalent to the homoskeskasticity-only F -statistic in Equation (7.13).
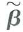 be the value of b that solves the constrained minimization problem.
be the value of b that solves the constrained minimization problem.a. Show that the Lagrangian for the minimization problem is L(b , ) = ( Y- Xb ) ' ( Y-Xb ) + ' ( Rb - r ), where is a q × 1 vector of Lagrange multipliers.
b. Show that
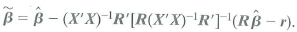
c. Show that
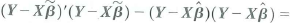
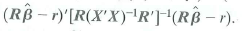
d. Show that F in Equation (18.36) is equivalent to the homoskeskasticity-only F -statistic in Equation (7.13).
Explanation
a) The minimization is
However it is c...
Introduction to Econometrics 3rd Edition by James Stock, Mark Watson
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255



