Chat with AI
Optical Fiber Communications 4th Edition by Gerd Keiser
Edition 4ISBN: 978-0073380711Optical Fiber Communications 4th Edition by Gerd Keiser
Edition 4ISBN: 978-0073380711 Exercise 18
Assume a given mode in a graded-index fiber has a power density p ( r ) = P0exp( -Kr 2 ), where the factor K depends on the modal power distribution.
( a ) Letting n ( r ) in Eq. (3.11) be given by Eq. (2.78) with = 2, show that the loss in this mode is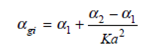
Since p ( r ) is a rapidly decaying function of r and since 1, for ease of calculation assume that the top relation in Eq. (2.78) holds for all values of r.
( b ) Choose K such that p ( a ) = 0.1 P0; that is, 10 percent of the power flows in the cladding. Find gi in terms of 1 and 2.
( a ) Letting n ( r ) in Eq. (3.11) be given by Eq. (2.78) with = 2, show that the loss in this mode is
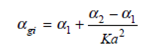
Since p ( r ) is a rapidly decaying function of r and since 1, for ease of calculation assume that the top relation in Eq. (2.78) holds for all values of r.
( b ) Choose K such that p ( a ) = 0.1 P0; that is, 10 percent of the power flows in the cladding. Find gi in terms of 1 and 2.
Explanation
Verified
Verified
(a) We want to solve Eq. (3.12) for gi. ...
Optical Fiber Communications 4th Edition by Gerd Keiser
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255
