
Introduction to Econometrics 3rd Edition by James Stock, James Stock
Edition 3ISBN: 978-9352863501
Introduction to Econometrics 3rd Edition by James Stock, James Stock
Edition 3ISBN: 978-9352863501 Exercise 3
A survey of 1055 registered voters is conducted, and the voters are asked to choose between candidate A and candidate B. Let p denote the fraction of voters in the population who prefer candidate A, and let 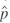 denote the fraction of voters in the sample who prefer Candidate A.
denote the fraction of voters in the sample who prefer Candidate A.
a. You are interested in the competing hypotheses H 0. p = 0.5 vs. H 1. p 0.5. Suppose that you decide to reject H 0 if | - 0.5| 0.02.
- 0.5| 0.02.
i. What is the size of this test
ii. Compute the power of this test if p = 0.53.
b. In the survey,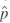 = 0.54.
= 0.54.
i. Test H 0 : p = 0.5 vs. H 1 p 0.5 using a 5% significance level.
ii. Test H 0 : p = 0.5 vs. Up p 0.5 using a 5% significance level.
iii. Construct a 95% confidence interval for p.
iv. Construct a 99% confidence interval for p.
v. Construct a 50% confidence interval for p.
c. Suppose that the survey is carried out 20 times, using independently selected voters in each survey. For each of these 20 surveys, a 95% confidence interval for p is constructed.
i. What is the probability that the true value of p is contained in all 20 of these confidence intervals
ii. How many of these confidence intervals do you expect to contain the true value of p
d. In survey jargon, the "margin of error" is 1.96 × SE( ); that is, it is half the length of 95% confidence interval. Suppose you wanted to design a survey that had a margin of error of at most 1%. That is, you wanted Pr(|
); that is, it is half the length of 95% confidence interval. Suppose you wanted to design a survey that had a margin of error of at most 1%. That is, you wanted Pr(| 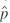 - p | 0.01) 0.05. How large should n be if the survey uses simple random sampling
- p | 0.01) 0.05. How large should n be if the survey uses simple random sampling
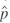 denote the fraction of voters in the sample who prefer Candidate A.
denote the fraction of voters in the sample who prefer Candidate A.a. You are interested in the competing hypotheses H 0. p = 0.5 vs. H 1. p 0.5. Suppose that you decide to reject H 0 if |
 - 0.5| 0.02.
- 0.5| 0.02.i. What is the size of this test
ii. Compute the power of this test if p = 0.53.
b. In the survey,
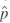 = 0.54.
= 0.54.i. Test H 0 : p = 0.5 vs. H 1 p 0.5 using a 5% significance level.
ii. Test H 0 : p = 0.5 vs. Up p 0.5 using a 5% significance level.
iii. Construct a 95% confidence interval for p.
iv. Construct a 99% confidence interval for p.
v. Construct a 50% confidence interval for p.
c. Suppose that the survey is carried out 20 times, using independently selected voters in each survey. For each of these 20 surveys, a 95% confidence interval for p is constructed.
i. What is the probability that the true value of p is contained in all 20 of these confidence intervals
ii. How many of these confidence intervals do you expect to contain the true value of p
d. In survey jargon, the "margin of error" is 1.96 × SE(
 ); that is, it is half the length of 95% confidence interval. Suppose you wanted to design a survey that had a margin of error of at most 1%. That is, you wanted Pr(|
); that is, it is half the length of 95% confidence interval. Suppose you wanted to design a survey that had a margin of error of at most 1%. That is, you wanted Pr(| 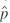 - p | 0.01) 0.05. How large should n be if the survey uses simple random sampling
- p | 0.01) 0.05. How large should n be if the survey uses simple random samplingExplanation
We are told that a survey of 1055 regist...
Introduction to Econometrics 3rd Edition by James Stock, James Stock
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255



