
Introduction to Econometrics 3rd Edition by James Stock, James Stock
Edition 3ISBN: 978-9352863501
Introduction to Econometrics 3rd Edition by James Stock, James Stock
Edition 3ISBN: 978-9352863501 Exercise 19
Assume that the regression model Y i = 0 + 1 X i + u i satisfies the least squares assumptions in Key Concept 4.3 in Section 4.4. You and a friend collect a random sample of 300 observations on Y and X.
a. Your friend reports the he inadvertently scrambled the X observations for 20% of the sample. For these scrambled observations, the value of X does not correspond to X i for the i th observation, but rather to the value of X for some other observation. In the notation of Section 9.2, the measured value of the regressor,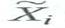 is equal to X i for 80% of the observations, but is equal to a randomly selected X j for the remaining 20% of the observations. You regress Y i on
is equal to X i for 80% of the observations, but is equal to a randomly selected X j for the remaining 20% of the observations. You regress Y i on 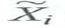 .
. 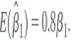
b. Explain how you could construct an unbiased estimate of ß x using the OLS estimator in (a).
c. Suppose now that your friend tells you that the X's were scrambled for the first 60 observations, but that the remaining 240 observations are correct. You estimate ß 1 by regressing Y on X using only the correctly measured 240 observations. Is this estimator of ß 1 better than the estimator you proposed in (b) Explain.
a. Your friend reports the he inadvertently scrambled the X observations for 20% of the sample. For these scrambled observations, the value of X does not correspond to X i for the i th observation, but rather to the value of X for some other observation. In the notation of Section 9.2, the measured value of the regressor,
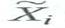 is equal to X i for 80% of the observations, but is equal to a randomly selected X j for the remaining 20% of the observations. You regress Y i on
is equal to X i for 80% of the observations, but is equal to a randomly selected X j for the remaining 20% of the observations. You regress Y i on 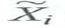 .
. 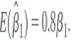
b. Explain how you could construct an unbiased estimate of ß x using the OLS estimator in (a).
c. Suppose now that your friend tells you that the X's were scrambled for the first 60 observations, but that the remaining 240 observations are correct. You estimate ß 1 by regressing Y on X using only the correctly measured 240 observations. Is this estimator of ß 1 better than the estimator you proposed in (b) Explain.

Explanation
b) Since the bias has a factor of 0.8, t...
Introduction to Econometrics 3rd Edition by James Stock, James Stock
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255



