
Introduction to Econometrics 3rd Edition by James Stock, James Stock
Edition 3ISBN: 978-9352863501
Introduction to Econometrics 3rd Edition by James Stock, James Stock
Edition 3ISBN: 978-9352863501 Exercise 15
Consider the heterogeneous regression model 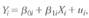 where 0i and 1i are random variables that differ from one observation to the next. Suppose that
where 0i and 1i are random variables that differ from one observation to the next. Suppose that 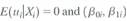 are distributed independently of X i.
are distributed independently of X i.
a. Let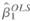 denote the OLS estimator of 1 given in Equation (17.2). Show that
denote the OLS estimator of 1 given in Equation (17.2). Show that 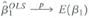 , where E ( 1 ) is the average value of 1 i in the population.
, where E ( 1 ) is the average value of 1 i in the population.
b. Suppose that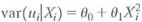 , where 0 and 1 are known positive constants. Let
, where 0 and 1 are known positive constants. Let 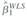 denote the weighted least squares estimator. Does
denote the weighted least squares estimator. Does 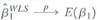 Explain.
Explain. 
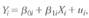 where 0i and 1i are random variables that differ from one observation to the next. Suppose that
where 0i and 1i are random variables that differ from one observation to the next. Suppose that 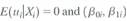 are distributed independently of X i.
are distributed independently of X i. a. Let
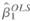 denote the OLS estimator of 1 given in Equation (17.2). Show that
denote the OLS estimator of 1 given in Equation (17.2). Show that 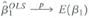 , where E ( 1 ) is the average value of 1 i in the population.
, where E ( 1 ) is the average value of 1 i in the population.b. Suppose that
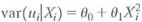 , where 0 and 1 are known positive constants. Let
, where 0 and 1 are known positive constants. Let 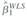 denote the weighted least squares estimator. Does
denote the weighted least squares estimator. Does 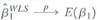 Explain.
Explain. 
Explanation
a) The heterogeneous regression is The ...
Introduction to Econometrics 3rd Edition by James Stock, James Stock
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255



