Deck 7: Linear Programming Models: Graphical and Computer Methods
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/100
Play
Full screen (f)
Deck 7: Linear Programming Models: Graphical and Computer Methods
1
In some instances, an infeasible solution may be the optimum found by the corner point method.
False
2
When two or more constraints conflict with one another, we have a condition called unboundedness.
False
3
Management resources that need control include machinery usage, labor volume, money spent, time used, warehouse space used, and material usage.
True
4
In a linear program, the constraints must be linear, but the objective function may be nonlinear.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
5
Any time that we have an isoprofit line that is parallel to a constraint, we have the possibility of multiple solutions.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
6
There are no limitations on the number of constraints or variables that can be graphed to solve an LP problem.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
7
Resource restrictions are called constraints.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
8
An objective function is necessary in a maximization problem but is not required in a minimization problem.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
9
The solution to a linear programming problem must always lie on a constraint.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
10
The set of solution points that satisfies all of a linear programming problem's constraints simultaneously is defined as the feasible region in graphical linear programming.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
11
Resource mix problems use LP to decide how much of each product to make, given a series of resource restrictions.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
12
In the term linear programming, the word programming comes from the phrase "computer programming."

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
13
If the isoprofit line is not parallel to a constraint, then the solution must be unique.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
14
The existence of non-negativity constraints in a two-variable linear program implies that we are always working in the northwest quadrant of a graph.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
15
One of the assumptions of LP is "proportionality."

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
16
Any linear programming problem can be solved using the graphical solution procedure.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
17
The rationality assumption implies that solutions need not be in whole numbers (integers).

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
18
An LP formulation typically requires finding the maximum value of an objective while simultaneously maximizing usage of the resource constraints.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
19
In linear programming terminology, "dual price" and "sensitivity price" are synonyms.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
20
One of the assumptions of LP is "simultaneity."

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
21
In a maximization problem, when one or more of the solution variables and the profit can be made infinitely large without violating any constraints, the linear program has
A) an infeasible solution.
B) an unbounded solution.
C) a redundant constraint.
D) alternate optimal solutions.
E) None of the above
A) an infeasible solution.
B) an unbounded solution.
C) a redundant constraint.
D) alternate optimal solutions.
E) None of the above

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
22
A feasible solution to a linear programming problem
A) must be a corner point of the feasible region.
B) must satisfy all of the problem's constraints simultaneously.
C) need not satisfy all of the constraints, only the non-negativity constraints.
D) must give the maximum possible profit.
E) must give the minimum possible cost.
A) must be a corner point of the feasible region.
B) must satisfy all of the problem's constraints simultaneously.
C) need not satisfy all of the constraints, only the non-negativity constraints.
D) must give the maximum possible profit.
E) must give the minimum possible cost.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
23
Consider the following linear programming problem: 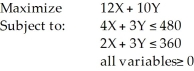 The maximum possible value for the objective function is
The maximum possible value for the objective function is
A) 360.
B) 480.
C) 1520.
D) 1560.
E) None of the above
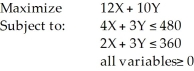 The maximum possible value for the objective function is
The maximum possible value for the objective function isA) 360.
B) 480.
C) 1520.
D) 1560.
E) None of the above

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
24
The mathematical theory behind linear programming states that an optimal solution to any problem will lie at a(n) ________ of the feasible region.
A) interior point or center
B) maximum point or minimum point
C) corner point or extreme point
D) interior point or extreme point
E) None of the above
A) interior point or center
B) maximum point or minimum point
C) corner point or extreme point
D) interior point or extreme point
E) None of the above

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
25
The simultaneous equation method is
A) an alternative to the corner point method.
B) useful only in minimization methods.
C) an algebraic means for solving the intersection of two or more constraint equations.
D) useful only when more than two product variables exist in a product mix problem.
E) None of the above
A) an alternative to the corner point method.
B) useful only in minimization methods.
C) an algebraic means for solving the intersection of two or more constraint equations.
D) useful only when more than two product variables exist in a product mix problem.
E) None of the above

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
26
Which of the following is not a property of linear programs?
A) one objective function
B) at least two separate feasible regions
C) alternative courses of action
D) one or more constraints
E) objective function and constraints are linear
A) one objective function
B) at least two separate feasible regions
C) alternative courses of action
D) one or more constraints
E) objective function and constraints are linear

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
27
Sensitivity analysis enables us to look at the effects of changing the coefficients in the objective function, one at a time.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
28
Infeasibility in a linear programming problem occurs when
A) there is an infinite solution.
B) a constraint is redundant.
C) more than one solution is optimal.
D) the feasible region is unbounded.
E) there is no solution that satisfies all the constraints given.
A) there is an infinite solution.
B) a constraint is redundant.
C) more than one solution is optimal.
D) the feasible region is unbounded.
E) there is no solution that satisfies all the constraints given.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
29
When a constraint line bounding a feasible region has the same slope as an isoprofit line,
A) there may be more than one optimum solution.
B) the problem involves redundancy.
C) an error has been made in the problem formulation.
D) a condition of infeasibility exists.
E) None of the above
A) there may be more than one optimum solution.
B) the problem involves redundancy.
C) an error has been made in the problem formulation.
D) a condition of infeasibility exists.
E) None of the above

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
30
The addition of a redundant constraint lowers the isoprofit line.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
31
Which of the following is not a part of every linear programming problem formulation?
A) an objective function
B) a set of constraints
C) non-negativity constraints
D) a redundant constraint
E) maximization or minimization of a linear function
A) an objective function
B) a set of constraints
C) non-negativity constraints
D) a redundant constraint
E) maximization or minimization of a linear function

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
32
Two models of a product - Regular (X) and Deluxe (Y) - are produced by a company. A linear programming model is used to determine the production schedule. The formulation is as follows: 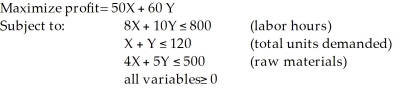 The optimal solution is X = 100, Y = 0. How many units of the regular model would be produced based on this solution?
The optimal solution is X = 100, Y = 0. How many units of the regular model would be produced based on this solution?
A) 0
B) 100
C) 50
D) 120
E) None of the above
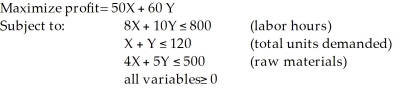 The optimal solution is X = 100, Y = 0. How many units of the regular model would be produced based on this solution?
The optimal solution is X = 100, Y = 0. How many units of the regular model would be produced based on this solution?A) 0
B) 100
C) 50
D) 120
E) None of the above

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
33
The corner point solution method
A) will always provide one, and only one, optimum.
B) will yield different results from the isoprofit line solution method.
C) requires that the profit from all corners of the feasible region be compared.
D) requires that all corners created by all constraints be compared.
E) will not provide a solution at an intersection or corner where a non-negativity constraint is involved.
A) will always provide one, and only one, optimum.
B) will yield different results from the isoprofit line solution method.
C) requires that the profit from all corners of the feasible region be compared.
D) requires that all corners created by all constraints be compared.
E) will not provide a solution at an intersection or corner where a non-negativity constraint is involved.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
34
Typical resources of an organization include ________.
A) machinery usage
B) labor volume
C) warehouse space utilization
D) raw material usage
E) All of the above
A) machinery usage
B) labor volume
C) warehouse space utilization
D) raw material usage
E) All of the above

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
35
When appropriate, the optimal solution to a maximization linear programming problem can be found by graphing the feasible region and
A) finding the profit at every corner point of the feasible region to see which one gives the highest value.
B) moving the isoprofit lines towards the origin in a parallel fashion until the last point in the feasible region is encountered.
C) locating the point that is highest on the graph.
D) None of the above
E) All of the above
A) finding the profit at every corner point of the feasible region to see which one gives the highest value.
B) moving the isoprofit lines towards the origin in a parallel fashion until the last point in the feasible region is encountered.
C) locating the point that is highest on the graph.
D) None of the above
E) All of the above

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
36
Consider the following linear programming problem: 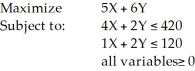 Which of the following points (X,Y) is not feasible?
Which of the following points (X,Y) is not feasible?
A) (50,40)
B) (20,50)
C) (60,30)
D) (90,10)
E) None of the above
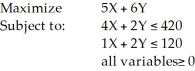 Which of the following points (X,Y) is not feasible?
Which of the following points (X,Y) is not feasible?A) (50,40)
B) (20,50)
C) (60,30)
D) (90,10)
E) None of the above

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
37
Consider the following linear programming problem: 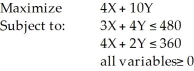 The feasible corner points are (48,84), (0,120), (0,0), (90,0). What is the maximum possible value for the objective function?
The feasible corner points are (48,84), (0,120), (0,0), (90,0). What is the maximum possible value for the objective function?
A) 1032
B) 1200
C) 360
D) 1600
E) None of the above
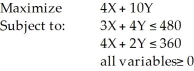 The feasible corner points are (48,84), (0,120), (0,0), (90,0). What is the maximum possible value for the objective function?
The feasible corner points are (48,84), (0,120), (0,0), (90,0). What is the maximum possible value for the objective function?A) 1032
B) 1200
C) 360
D) 1600
E) None of the above

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
38
Consider the following linear programming problem: 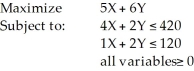 Which of the following points (X,Y) is not a feasible corner point?
Which of the following points (X,Y) is not a feasible corner point?
A) (0,60)
B) (105,0)
C) (120,0)
D) (100,10)
E) None of the above
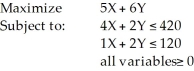 Which of the following points (X,Y) is not a feasible corner point?
Which of the following points (X,Y) is not a feasible corner point?A) (0,60)
B) (105,0)
C) (120,0)
D) (100,10)
E) None of the above

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
39
A widely used mathematical programming technique designed to help managers and decision making relative to resource allocation is called ________.
A) linear programming
B) computer programming
C) constraint programming
D) goal programming
E) None of the above
A) linear programming
B) computer programming
C) constraint programming
D) goal programming
E) None of the above

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
40
Which of the following is not a property of all linear programming problems?
A) the presence of restrictions
B) optimization of some objective
C) a computer program
D) alternate courses of action to choose from
E) usage of only linear equations and inequalities
A) the presence of restrictions
B) optimization of some objective
C) a computer program
D) alternate courses of action to choose from
E) usage of only linear equations and inequalities

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
41
Consider the following linear programming problem: 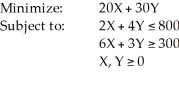 What is the optimum solution to this problem (X,Y)?
What is the optimum solution to this problem (X,Y)?
A) (0,0)
B) (50,0)
C) (0,100)
D) (400,0)
E) None of the above
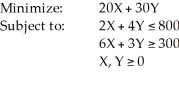 What is the optimum solution to this problem (X,Y)?
What is the optimum solution to this problem (X,Y)?A) (0,0)
B) (50,0)
C) (0,100)
D) (400,0)
E) None of the above

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
42
If one changes the contribution rates in the objective function of an LP,
A) the feasible region will change.
B) the slope of the isoprofit or isocost line will change.
C) the optimal solution to the LP is sure to no longer be optimal.
D) All of the above
E) None of the above
A) the feasible region will change.
B) the slope of the isoprofit or isocost line will change.
C) the optimal solution to the LP is sure to no longer be optimal.
D) All of the above
E) None of the above

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
43
Consider the following linear programming problem: 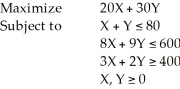 This is a special case of a linear programming problem in which
This is a special case of a linear programming problem in which
A) there is no feasible solution.
B) there is a redundant constraint.
C) there are multiple optimal solutions.
D) this cannot be solved graphically.
E) None of the above
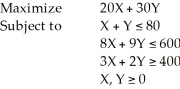 This is a special case of a linear programming problem in which
This is a special case of a linear programming problem in whichA) there is no feasible solution.
B) there is a redundant constraint.
C) there are multiple optimal solutions.
D) this cannot be solved graphically.
E) None of the above

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
44
A constraint with positive slack or surplus is called a
A) nonbinding constraint.
B) resource constraint.
C) binding constraint.
D) nonlinear constraint.
E) linear constraint.
A) nonbinding constraint.
B) resource constraint.
C) binding constraint.
D) nonlinear constraint.
E) linear constraint.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
45
The difference between the left-hand side and right-hand side of a less-than-or-equal-to constraint is referred to as
A) surplus.
B) constraint.
C) slack.
D) shadow price.
E) None of the above
A) surplus.
B) constraint.
C) slack.
D) shadow price.
E) None of the above

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
46
Sensitivity analysis may also be called
A) postoptimality analysis.
B) parametric programming.
C) optimality analysis.
D) All of the above
E) None of the above
A) postoptimality analysis.
B) parametric programming.
C) optimality analysis.
D) All of the above
E) None of the above

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
47
Sensitivity analyses are used to examine the effects of changes in
A) contribution rates for each variable.
B) technological coefficients.
C) available resources.
D) All of the above
E) None of the above
A) contribution rates for each variable.
B) technological coefficients.
C) available resources.
D) All of the above
E) None of the above

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
48
Consider the following linear programming problem: 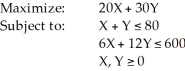 This is a special case of a linear programming problem in which
This is a special case of a linear programming problem in which
A) there is no feasible solution.
B) there is a redundant constraint.
C) there are multiple optimal solutions.
D) this cannot be solved graphically.
E) None of the above
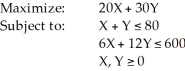 This is a special case of a linear programming problem in which
This is a special case of a linear programming problem in whichA) there is no feasible solution.
B) there is a redundant constraint.
C) there are multiple optimal solutions.
D) this cannot be solved graphically.
E) None of the above

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
49
In order for a linear programming problem to have multiple solutions, the solution must exist
A) at the intersection of the non-negativity constraints.
B) on a non-redundant constraint parallel to the objective function.
C) at the intersection of the objective function and a constraint.
D) at the intersection of three or more constraints.
E) None of the above
A) at the intersection of the non-negativity constraints.
B) on a non-redundant constraint parallel to the objective function.
C) at the intersection of the objective function and a constraint.
D) at the intersection of three or more constraints.
E) None of the above

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
50
The increase in the objective function value that results from a one-unit increase in the right-hand side of that constraint is called
A) surplus.
B) shadow price.
C) slack.
D) dual price.
E) None of the above
A) surplus.
B) shadow price.
C) slack.
D) dual price.
E) None of the above

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
51
The difference between the left-hand side and right-hand side of a greater-than-or-equal-to constraint is referred to as
A) surplus.
B) constraint.
C) slack.
D) shadow price.
E) None of the above
A) surplus.
B) constraint.
C) slack.
D) shadow price.
E) None of the above

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
52
Which of the following is not an assumption of LP?
A) simultaneity
B) certainty
C) proportionality
D) divisibility
E) additivity
A) simultaneity
B) certainty
C) proportionality
D) divisibility
E) additivity

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
53
In order for a linear programming problem to have a unique solution, the solution must exist
A) at the intersection of the non-negativity constraints.
B) at the intersection of a non-negativity constraint and a resource constraint.
C) at the intersection of the objective function and a constraint.
D) at the intersection of two or more constraints.
E) None of the above
A) at the intersection of the non-negativity constraints.
B) at the intersection of a non-negativity constraint and a resource constraint.
C) at the intersection of the objective function and a constraint.
D) at the intersection of two or more constraints.
E) None of the above

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
54
A straight line representing all non-negative combinations of X1 and X2 for a particular profit level is called a(n)
A) constraint line.
B) objective line.
C) sensitivity line.
D) profit line.
E) isoprofit line.
A) constraint line.
B) objective line.
C) sensitivity line.
D) profit line.
E) isoprofit line.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
55
The condition when there is no solution that satisfies all the constraints simultaneously is called
A) boundedness.
B) redundancy.
C) optimality.
D) dependency.
E) None of the above
A) boundedness.
B) redundancy.
C) optimality.
D) dependency.
E) None of the above

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
56
Which of the following is a basic assumption of linear programming?
A) The condition of uncertainty exists.
B) Independence exists for the activities.
C) Proportionality exists in the objective function and constraints.
D) Divisibility does not exist, allowing only integer solutions.
E) Solutions or variables may take values from -∞ to +∞.
A) The condition of uncertainty exists.
B) Independence exists for the activities.
C) Proportionality exists in the objective function and constraints.
D) Divisibility does not exist, allowing only integer solutions.
E) Solutions or variables may take values from -∞ to +∞.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
57
Which of the following is not acceptable as a constraint in a linear programming problem (maximization)? 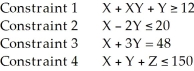
A) Constraint 1
B) Constraint 2
C) Constraint 3
D) Constraint 4
E) None of the above
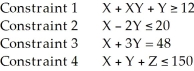
A) Constraint 1
B) Constraint 2
C) Constraint 3
D) Constraint 4
E) None of the above

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
58
Two models of a product - Regular (X) and Deluxe (Y) - are produced by a company. A linear programming model is used to determine the production schedule. The formulation is as follows: 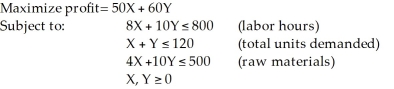 The optimal solution is X=100, Y=0. Which of these constraints is redundant?
The optimal solution is X=100, Y=0. Which of these constraints is redundant?
A) the first constraint
B) the second constraint
C) the third constraint
D) All of the above
E) None of the above
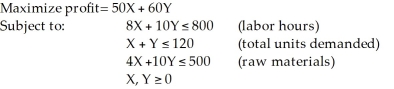 The optimal solution is X=100, Y=0. Which of these constraints is redundant?
The optimal solution is X=100, Y=0. Which of these constraints is redundant?A) the first constraint
B) the second constraint
C) the third constraint
D) All of the above
E) None of the above

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
59
If the addition of a constraint to a linear programming problem does not change the solution, the constraint is said to be
A) unbounded.
B) non-negative.
C) infeasible.
D) redundant.
E) bounded.
A) unbounded.
B) non-negative.
C) infeasible.
D) redundant.
E) bounded.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
60
A constraint with zero slack or surplus is called a
A) nonbinding constraint.
B) resource constraint.
C) binding constraint.
D) nonlinear constraint.
E) linear constraint.
A) nonbinding constraint.
B) resource constraint.
C) binding constraint.
D) nonlinear constraint.
E) linear constraint.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
61
Consider the following constraints from a linear programming problem: 2X + Y ≤ 200
X + 2Y ≤ 200
X, Y ≥ 0
If these are the only constraints, which of the following points (X,Y) cannot be the optimal solution?
A) (0, 0)
B) (0, 200)
C) (0,100)
D) (100, 0)
E) (66.67, 66.67)
X + 2Y ≤ 200
X, Y ≥ 0
If these are the only constraints, which of the following points (X,Y) cannot be the optimal solution?
A) (0, 0)
B) (0, 200)
C) (0,100)
D) (100, 0)
E) (66.67, 66.67)

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
62
Solve the following linear programming problem using the corner point method: 


Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
63
A furniture company is producing two types of furniture. Product A requires 8 board feet of wood and 2 lbs of wicker. Product B requires 6 board feet of wood and 6 lbs of wicker. There are 2000 board feet of wood available for product and 1000 lbs of wicker. Product A earns a profit margin of $30 a unit and Product B earns a profit margin of $40 a unit. Formulate the problem as a linear program.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
64
The Fido Dog Food Company wishes to introduce a new brand of dog biscuits (composed of chicken and liver-flavored biscuits) that meets certain nutritional requirements. The liver-flavored biscuits contain 1 unit of nutrient A and 2 units of nutrient B, while the chicken-flavored ones contain 1 unit of nutrient A and 4 units of nutrient B. According to federal requirements, there must be at least 40 units of nutrient A and 60 units of nutrient B in a package of the new biscuit mix. In addition, the company has decided that there can be no more than 15 liver-flavored biscuits in a package. If it costs 1 cent to make a liver-flavored biscuit and 2 cents to make a chicken-flavored one, what is the optimal product mix for a package of the biscuits in order to minimize the firm's cost?
(a) Formulate this as a linear programming problem.
(b) Find the optimal solution for this problem graphically.
(c) Are any constraints redundant? If so, which one or ones?
(d) What is the total cost of a package of dog biscuits using the optimal mix?
(a) Formulate this as a linear programming problem.
(b) Find the optimal solution for this problem graphically.
(c) Are any constraints redundant? If so, which one or ones?
(d) What is the total cost of a package of dog biscuits using the optimal mix?

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
65
Which of the following functions is not linear?
A) 5X + 3Z
B) 3X + 4Y + Z - 3
C) 2X + 5YZ
D) Z
E) 2X - 5Y + 2Z
A) 5X + 3Z
B) 3X + 4Y + Z - 3
C) 2X + 5YZ
D) Z
E) 2X - 5Y + 2Z

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
66
Consider the following linear programming problem: 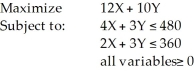 Which of the following points (X,Y) is feasible?
Which of the following points (X,Y) is feasible?
A) (10,120)
B) (120,10)
C) (30,100)
D) (60,90)
E) None of the above
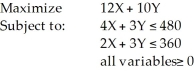 Which of the following points (X,Y) is feasible?
Which of the following points (X,Y) is feasible?A) (10,120)
B) (120,10)
C) (30,100)
D) (60,90)
E) None of the above

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
67
Consider the following constraints from a linear programming problem: 2X + Y ≤ 200
X + 2Y ≤ 200
X, Y ≥ 0
If these are the only constraints, which of the following points (X,Y) cannot be the optimal solution?
A) (0, 0)
B) (0, 100)
C) (65, 65)
D) (100, 0)
E) (66.67, 66.67)
X + 2Y ≤ 200
X, Y ≥ 0
If these are the only constraints, which of the following points (X,Y) cannot be the optimal solution?
A) (0, 0)
B) (0, 100)
C) (65, 65)
D) (100, 0)
E) (66.67, 66.67)

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
68
Solve the following linear programming problem using the corner point method: 


Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
69
Consider the following linear programming problem: 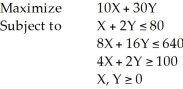 This is a special case of a linear programming problem in which
This is a special case of a linear programming problem in which
A) there is no feasible solution.
B) there is a redundant constraint.
C) there are multiple optimal solutions.
D) this cannot be solved graphically.
E) None of the above
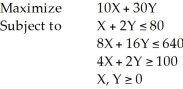 This is a special case of a linear programming problem in which
This is a special case of a linear programming problem in whichA) there is no feasible solution.
B) there is a redundant constraint.
C) there are multiple optimal solutions.
D) this cannot be solved graphically.
E) None of the above

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
70
Which of the following is not an assumption of LP?
A) certainty
B) proportionality
C) divisibility
D) multiplicativity
E) additivity
A) certainty
B) proportionality
C) divisibility
D) multiplicativity
E) additivity

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
71
Consider the following linear program: 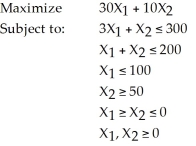 (a) Solve the problem graphically. Is there more than one optimal solution? Explain.
(a) Solve the problem graphically. Is there more than one optimal solution? Explain.
(b) Are there any redundant constraints?
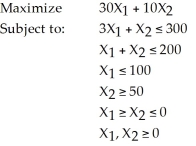 (a) Solve the problem graphically. Is there more than one optimal solution? Explain.
(a) Solve the problem graphically. Is there more than one optimal solution? Explain.(b) Are there any redundant constraints?

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
72
As a supervisor of a production department, you must decide the daily production totals of a certain product that has two models, the Deluxe and the Special. The profit on the Deluxe model is $12 per unit and the Special's profit is $10. Each model goes through two phases in the production process, and there are only 100 hours available daily at the construction stage and only 80 hours available at the finishing and inspection stage. Each Deluxe model requires 20 minutes of construction time and 10 minutes of finishing and inspection time. Each Special model requires 15 minutes of construction time and 15 minutes of finishing and inspection time. The company has also decided that the Special model must comprise at least 40 percent of the production total.
(a) Formulate this as a linear programming problem.
(b) Find the solution that gives the maximum profit.
(a) Formulate this as a linear programming problem.
(b) Find the solution that gives the maximum profit.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
73
Consider the following linear programming problem: 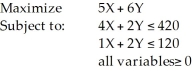 Which of the following points (X,Y) is feasible?
Which of the following points (X,Y) is feasible?
A) (50,40)
B) (30,50)
C) (60,30)
D) (90,20)
E) None of the above
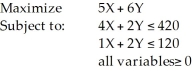 Which of the following points (X,Y) is feasible?
Which of the following points (X,Y) is feasible?A) (50,40)
B) (30,50)
C) (60,30)
D) (90,20)
E) None of the above

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
74
Billy Penny is trying to determine how many units of two types of lawn mowers to produce each day. One of these is the Standard model, while the other is the Deluxe model. The profit per unit on the Standard model is $60, while the profit per unit on the Deluxe model is $40. The Standard model requires 20 minutes of assembly time, while the Deluxe model requires 35 minutes of assembly time. The Standard model requires 10 minutes of inspection time, while the Deluxe model requires 15 minutes of inspection time. The company must fill an order for 6 Deluxe models. There are 450 minutes of assembly time and 180 minutes of inspection time available each day. How many units of each product should be manufactured to maximize profits?

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
75
Which of the following is not one of the steps in formulating a linear program?
A) Graph the constraints to determine the feasible region.
B) Define the decision variables.
C) Use the decision variables to write mathematical expressions for the objective function and the constraints.
D) Identify the objective and the constraints.
E) Completely understand the managerial problem being faced.
A) Graph the constraints to determine the feasible region.
B) Define the decision variables.
C) Use the decision variables to write mathematical expressions for the objective function and the constraints.
D) Identify the objective and the constraints.
E) Completely understand the managerial problem being faced.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
76
Which of the following is not acceptable as a constraint in a linear programming problem (minimization)? 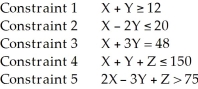
A) Constraint 1
B) Constraint 2
C) Constraint 3
D) Constraint 4
E) Constraint 5
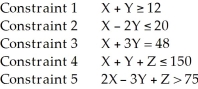
A) Constraint 1
B) Constraint 2
C) Constraint 3
D) Constraint 4
E) Constraint 5

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
77
Consider the following linear programming problem: 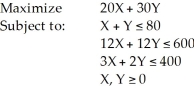 This is a special case of a linear programming problem in which
This is a special case of a linear programming problem in which
A) there is no feasible solution.
B) there is a redundant constraint.
C) there are multiple optimal solutions.
D) this cannot be solved graphically.
E) None of the above
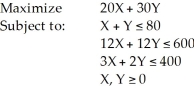 This is a special case of a linear programming problem in which
This is a special case of a linear programming problem in whichA) there is no feasible solution.
B) there is a redundant constraint.
C) there are multiple optimal solutions.
D) this cannot be solved graphically.
E) None of the above

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
78
Consider the following linear programming problem:  Which of the following points (X,Y) is in the feasible region?
Which of the following points (X,Y) is in the feasible region?
A) (30,60)
B) (105,5)
C) (0,210)
D) (100,10)
E) None of the above
 Which of the following points (X,Y) is in the feasible region?
Which of the following points (X,Y) is in the feasible region?A) (30,60)
B) (105,5)
C) (0,210)
D) (100,10)
E) None of the above

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
79
What type of problems use LP to decide how much of each product to make, given a series of resource restrictions?
A) resource mix
B) resource restriction
C) product restriction
D) resource allocation
E) product mix
A) resource mix
B) resource restriction
C) product restriction
D) resource allocation
E) product mix

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
80
Consider the following linear programming problem:  The maximum possible value for the objective function is
The maximum possible value for the objective function is
A) 360.
B) 480.
C) 1520.
D) 1560.
E) None of the above
 The maximum possible value for the objective function is
The maximum possible value for the objective function isA) 360.
B) 480.
C) 1520.
D) 1560.
E) None of the above

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck



