Deck 10: Integer Programming,goal Programming,and Nonlinear Programming
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/98
Play
Full screen (f)
Deck 10: Integer Programming,goal Programming,and Nonlinear Programming
1
Requiring an integer solution to a linear programming problem decreases the size of the feasible region.
True
2
In goal programming,the deviational variables have the same objective function coefficients as the surplus and slack variables in a normal linear program.
False
3
Unfortunately,goal programming,while able to handle multiple objectives,is unable to prioritize these objectives.
False
4
The following objective function is nonlinear: Max 5X - 8YZ.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
5
If conditions require that all decision variables must have an integer solution,then the class of problem described is an integer programming problem.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
6
There is no general method for solving all nonlinear problems.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
7
An integer programming solution can never produce a greater profit objective than the LP solution to the same problem.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
8
Nonlinear programming is the case in which objectives and/or constraints are nonlinear.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
9
The following objective function is nonlinear: Max 5X + (1/8)Y - Z.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
10
The constraint X1 + X2 ≤ 1 with 0 -1 integer programming allows for either X1 or X2 to be a part of the optimal solution,but not both.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
11
Quadratic programming contains squared terms in the constraints.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
12
Unfortunately,multiple goals in goal programming are not able to be prioritized and solved.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
13
0-1 integer programming might be applicable to selecting the best gymnastics team to represent a country from among all identified teams.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
14
In goal programming,our goal is to drive the deviational variables in the objective function as close to zero as possible.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
15
The transportation problem is a good example of a pure integer programming problem.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
16
When solving very large integer programming problems,we sometimes have to settle for a "good," not necessarily optimal,answer.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
17
In goal programming,if all the goals are achieved,then the value of the objective function will always be zero.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
18
The three types of integer programs are: pure integer programming,impure integer programming,and 0-1 integer programming.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
19
A 0-1 programming representation could be used to assign sections of a course to specific classrooms.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
20
Goal programming permits multiple objectives to be satisfied.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
21
Table 10-2
Maximize Z = 34 X1 + 43 X2 + 29 X3
Subject to: 5 X1 + 4 X2 + 7 X3 ≤ 50
1 X1 + 2 X2 + 2 X3 ≤ 16
3 X1 + 4 X2 + 1 X3 ≤ 9
all Xi are integer and non-negative
Final Integer Solution: Z = 208
Decision
Variable Solution
X1 1
X2 0
X3 6
According to Table 10-2,which presents a solution for an integer programming problem,at the optimal solution,how much slack exists in the third constraint?
A)0
B)9
C)5
D)6
E)-1
Maximize Z = 34 X1 + 43 X2 + 29 X3
Subject to: 5 X1 + 4 X2 + 7 X3 ≤ 50
1 X1 + 2 X2 + 2 X3 ≤ 16
3 X1 + 4 X2 + 1 X3 ≤ 9
all Xi are integer and non-negative
Final Integer Solution: Z = 208
Decision
Variable Solution
X1 1
X2 0
X3 6
According to Table 10-2,which presents a solution for an integer programming problem,at the optimal solution,how much slack exists in the third constraint?
A)0
B)9
C)5
D)6
E)-1

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
22
Table 10-1
A company has decided to use 0-1 integer programming to help make some investment decisions.There are three possible investment alternatives from which to choose,but if it is decided that a particular alternative is to be selected,the entire cost of that alternative will be incurred (i.e. ,it is impossible to build one-half of a factory).The integer programming model is as follows:
Maximize 5000 X1 + 7000X2 + 9000X3
Subject to: X1 + X2 + X3 ≤ 2 (only 2 may be chosen)
25000X1 + 32000X2 + 29000X3 ≤ 62,000 (budget limit)
16 X1 + 14 X2 + 19 X3 ≤ 36 (resource limitation)
all variables = 0 or 1
where X1 = 1 if alternative 1 is selected,0 otherwise
X2 = 1 if alternative 2 is selected,0 otherwise
X3 = 1 if alternative 3 is selected,0 otherwise
The optimal solution is X1 = 0,X2 = 1,X3 = 1
According to Table 10-1,which presents an integer programming problem,if the optimal solution is used,how much of the budget would be spent?
A)$32,000
B)$29,000
C)$61,000
D)$62,000
E)None of the above
A company has decided to use 0-1 integer programming to help make some investment decisions.There are three possible investment alternatives from which to choose,but if it is decided that a particular alternative is to be selected,the entire cost of that alternative will be incurred (i.e. ,it is impossible to build one-half of a factory).The integer programming model is as follows:
Maximize 5000 X1 + 7000X2 + 9000X3
Subject to: X1 + X2 + X3 ≤ 2 (only 2 may be chosen)
25000X1 + 32000X2 + 29000X3 ≤ 62,000 (budget limit)
16 X1 + 14 X2 + 19 X3 ≤ 36 (resource limitation)
all variables = 0 or 1
where X1 = 1 if alternative 1 is selected,0 otherwise
X2 = 1 if alternative 2 is selected,0 otherwise
X3 = 1 if alternative 3 is selected,0 otherwise
The optimal solution is X1 = 0,X2 = 1,X3 = 1
According to Table 10-1,which presents an integer programming problem,if the optimal solution is used,how much of the budget would be spent?
A)$32,000
B)$29,000
C)$61,000
D)$62,000
E)None of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
23
Table 10-1
A company has decided to use 0-1 integer programming to help make some investment decisions.There are three possible investment alternatives from which to choose,but if it is decided that a particular alternative is to be selected,the entire cost of that alternative will be incurred (i.e. ,it is impossible to build one-half of a factory).The integer programming model is as follows:
Maximize 5000 X1 + 7000X2 + 9000X3
Subject to: X1 + X2 + X3 ≤ 2 (only 2 may be chosen)
25000X1 + 32000X2 + 29000X3 ≤ 62,000 (budget limit)
16 X1 + 14 X2 + 19 X3 ≤ 36 (resource limitation)
all variables = 0 or 1
where X1 = 1 if alternative 1 is selected,0 otherwise
X2 = 1 if alternative 2 is selected,0 otherwise
X3 = 1 if alternative 3 is selected,0 otherwise
The optimal solution is X1 = 0,X2 = 1,X3 = 1
According to Table 10-1,which presents an integer programming problem,if the optimal solution is used,what would the value of the objective function be?
A)21,000
B)12,000
C)16,000
D)2
E)None of the above
A company has decided to use 0-1 integer programming to help make some investment decisions.There are three possible investment alternatives from which to choose,but if it is decided that a particular alternative is to be selected,the entire cost of that alternative will be incurred (i.e. ,it is impossible to build one-half of a factory).The integer programming model is as follows:
Maximize 5000 X1 + 7000X2 + 9000X3
Subject to: X1 + X2 + X3 ≤ 2 (only 2 may be chosen)
25000X1 + 32000X2 + 29000X3 ≤ 62,000 (budget limit)
16 X1 + 14 X2 + 19 X3 ≤ 36 (resource limitation)
all variables = 0 or 1
where X1 = 1 if alternative 1 is selected,0 otherwise
X2 = 1 if alternative 2 is selected,0 otherwise
X3 = 1 if alternative 3 is selected,0 otherwise
The optimal solution is X1 = 0,X2 = 1,X3 = 1
According to Table 10-1,which presents an integer programming problem,if the optimal solution is used,what would the value of the objective function be?
A)21,000
B)12,000
C)16,000
D)2
E)None of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
24
Which of the following functions is nonlinear?
A)4X + 2Y + 7Z
B)-4X + 2Y
C)4X + (1/2)Y + 7Z
D)Z
E)4X/Y + 7Z
A)4X + 2Y + 7Z
B)-4X + 2Y
C)4X + (1/2)Y + 7Z
D)Z
E)4X/Y + 7Z

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
25
Table 10-1
A company has decided to use 0-1 integer programming to help make some investment decisions.There are three possible investment alternatives from which to choose,but if it is decided that a particular alternative is to be selected,the entire cost of that alternative will be incurred (i.e. ,it is impossible to build one-half of a factory).The integer programming model is as follows:
Maximize 5000 X1 + 7000X2 + 9000X3
Subject to: X1 + X2 + X3 ≤ 2 (only 2 may be chosen)
25000X1 + 32000X2 + 29000X3 ≤ 62,000 (budget limit)
16 X1 + 14 X2 + 19 X3 ≤ 36 (resource limitation)
all variables = 0 or 1
where X1 = 1 if alternative 1 is selected,0 otherwise
X2 = 1 if alternative 2 is selected,0 otherwise
X3 = 1 if alternative 3 is selected,0 otherwise
The optimal solution is X1 = 0,X2 = 1,X3 = 1
According to Table 10-1,which presents an integer programming problem,the optimal solution is to select only two of the alternatives.Suppose you wished to add a constraint that stipulated that alternative 2 could only be selected if alternative 1 is also selected .How would this constraint be written?
A)X1 = X2
B)X1 ≤ X2
C)X1 ≥ X2
D)X1 + X2 = 2
E)None of the above
A company has decided to use 0-1 integer programming to help make some investment decisions.There are three possible investment alternatives from which to choose,but if it is decided that a particular alternative is to be selected,the entire cost of that alternative will be incurred (i.e. ,it is impossible to build one-half of a factory).The integer programming model is as follows:
Maximize 5000 X1 + 7000X2 + 9000X3
Subject to: X1 + X2 + X3 ≤ 2 (only 2 may be chosen)
25000X1 + 32000X2 + 29000X3 ≤ 62,000 (budget limit)
16 X1 + 14 X2 + 19 X3 ≤ 36 (resource limitation)
all variables = 0 or 1
where X1 = 1 if alternative 1 is selected,0 otherwise
X2 = 1 if alternative 2 is selected,0 otherwise
X3 = 1 if alternative 3 is selected,0 otherwise
The optimal solution is X1 = 0,X2 = 1,X3 = 1
According to Table 10-1,which presents an integer programming problem,the optimal solution is to select only two of the alternatives.Suppose you wished to add a constraint that stipulated that alternative 2 could only be selected if alternative 1 is also selected .How would this constraint be written?
A)X1 = X2
B)X1 ≤ X2
C)X1 ≥ X2
D)X1 + X2 = 2
E)None of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
26
A goal programming problem had two goals (with no priorities assigned).Goal number 1 was to achieve a profit of $3,600 and goal number 2 was to have no wasted material.The optimal solution to this problem resulted in a profit of $3,300 and no wasted material.What was the value for the objective function for this goal programming problem?
A)300
B)-300
C)3300
D)0
E)None of the above
A)300
B)-300
C)3300
D)0
E)None of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
27
An integer programming (minimization)problem was first solved as a linear programming problem,and the objective function value (cost)was $253.67.The two decision variables (X,Y)in the problem had values of X = 12.45 and Y = 32.75.If there is a single optimal solution,which of the following must be true for the optimal integer solution to this problem?
A)X = 13 Y = 33
B)X = 12 Y = 32
C)The objective function value must be less than $253.67.
D)The objective function value will be greater than $253.67.
E)None of the above
A)X = 13 Y = 33
B)X = 12 Y = 32
C)The objective function value must be less than $253.67.
D)The objective function value will be greater than $253.67.
E)None of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
28
Which of the following is a category of mathematical programming techniques that doesn't assume linearity in the objective function and/or constraints?
A)integer programs
B)goal programming problems
C)nonlinear programs
D)multiple objective programming problems
E)None of the above
A)integer programs
B)goal programming problems
C)nonlinear programs
D)multiple objective programming problems
E)None of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
29
In a goal programming problem with two goals at the same priority level,all the deviational variables are equal to zero in the optimal solution.This means
A)there is no feasible solution to the problem.
B)all goals are fully achieved.
C)nonlinear programming must be used to solve this.
D)this problem was an integer programming problem.
E)None of the above
A)there is no feasible solution to the problem.
B)all goals are fully achieved.
C)nonlinear programming must be used to solve this.
D)this problem was an integer programming problem.
E)None of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
30
Goal programming is characterized by
A)all maximization problems.
B)setting of lower and upper bounds.
C)the deviation from a high-priority goal must be minimized before the next-highest-priority goal may be considered.
D)All of the above
E)None of the above
A)all maximization problems.
B)setting of lower and upper bounds.
C)the deviation from a high-priority goal must be minimized before the next-highest-priority goal may be considered.
D)All of the above
E)None of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
31
A model containing a linear objective function and linear constraints but requiring that one or more of the decision variables take on an integer value in the final solution is called
A)a goal programming problem.
B)an integer programming problem.
C)a nonlinear programming problem.
D)a multiple objective LP problem.
E)a branch-and-bound programming problem.
A)a goal programming problem.
B)an integer programming problem.
C)a nonlinear programming problem.
D)a multiple objective LP problem.
E)a branch-and-bound programming problem.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
32
Goal programming differs from linear programming in which of the following aspects?
A)It tries to maximize deviations between set goals and what can be achieved within the constraints.
B)It minimizes instead of maximizing as in LP.
C)It permits multiple goals to be combined into one objective function.
D)All of the above
E)None of the above
A)It tries to maximize deviations between set goals and what can be achieved within the constraints.
B)It minimizes instead of maximizing as in LP.
C)It permits multiple goals to be combined into one objective function.
D)All of the above
E)None of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
33
We do not have a general method for solving all types of ________ problems.
A)mixed-integer programming
B)0-1 integer programming
C)goal programming
D)nonlinear programming
E)pure integer programming
A)mixed-integer programming
B)0-1 integer programming
C)goal programming
D)nonlinear programming
E)pure integer programming

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
34
A mathematical programming model that permits decision makers to set and prioritize multiple objective functions is called a
A)pure-integer programming problem.
B)mixed-integer programming problem.
C)zero-one integer programming problem.
D)goal programming problem.
E)nonlinear programming problem.
A)pure-integer programming problem.
B)mixed-integer programming problem.
C)zero-one integer programming problem.
D)goal programming problem.
E)nonlinear programming problem.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
35
An integer programming (maximization)problem was first solved as a linear programming problem,and the objective function value (profit)was $253.67.The two decision variables (X,Y)in the problem had values of X = 12.45 and Y = 32.75.If there is a single optimal solution,which of the following must be true for the optimal integer solution to this problem?
A)X = 12 Y = 32
B)X = 12 Y = 33
C)The objective function value must be less than $253.67.
D)The objective function value will be greater than $253.67.
E)None of the above
A)X = 12 Y = 32
B)X = 12 Y = 33
C)The objective function value must be less than $253.67.
D)The objective function value will be greater than $253.67.
E)None of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
36
In an integer programming problem,if it is desired to have variable X be exactly twice the value of variable Y,the constraint would be written
A)2X + Y = 0.
B)X + 2Y = 0.
C)2X - Y = 0.
D)X - 2Y = 0.
E)None of the above
A)2X + Y = 0.
B)X + 2Y = 0.
C)2X - Y = 0.
D)X - 2Y = 0.
E)None of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
37
A goal programming problem had two goals (with no priorities assigned).Goal number 1 was to achieve a profit of $2,400 and goal number 2 was to have no idle time for workers in the factory.The optimal solution to this problem resulted in a profit of $2,300 and no idle time.What was the value for the objective function for this goal programming problem?
A)2300
B)100
C)-100
D)0
E)None of the above
A)2300
B)100
C)-100
D)0
E)None of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
38
Table 10-1
A company has decided to use 0-1 integer programming to help make some investment decisions.There are three possible investment alternatives from which to choose,but if it is decided that a particular alternative is to be selected,the entire cost of that alternative will be incurred (i.e. ,it is impossible to build one-half of a factory).The integer programming model is as follows:
Maximize 5000 X1 + 7000X2 + 9000X3
Subject to: X1 + X2 + X3 ≤ 2 (only 2 may be chosen)
25000X1 + 32000X2 + 29000X3 ≤ 62,000 (budget limit)
16 X1 + 14 X2 + 19 X3 ≤ 36 (resource limitation)
all variables = 0 or 1
where X1 = 1 if alternative 1 is selected,0 otherwise
X2 = 1 if alternative 2 is selected,0 otherwise
X3 = 1 if alternative 3 is selected,0 otherwise
The optimal solution is X1 = 0,X2 = 1,X3 = 1
In Table 10-1,which presents an integer programming problem,using the optimal solution means only two of the alternatives would be selected.How much slack is there in the third constraint?
A)0
B)3
C)33
D)36
E)None of the above
A company has decided to use 0-1 integer programming to help make some investment decisions.There are three possible investment alternatives from which to choose,but if it is decided that a particular alternative is to be selected,the entire cost of that alternative will be incurred (i.e. ,it is impossible to build one-half of a factory).The integer programming model is as follows:
Maximize 5000 X1 + 7000X2 + 9000X3
Subject to: X1 + X2 + X3 ≤ 2 (only 2 may be chosen)
25000X1 + 32000X2 + 29000X3 ≤ 62,000 (budget limit)
16 X1 + 14 X2 + 19 X3 ≤ 36 (resource limitation)
all variables = 0 or 1
where X1 = 1 if alternative 1 is selected,0 otherwise
X2 = 1 if alternative 2 is selected,0 otherwise
X3 = 1 if alternative 3 is selected,0 otherwise
The optimal solution is X1 = 0,X2 = 1,X3 = 1
In Table 10-1,which presents an integer programming problem,using the optimal solution means only two of the alternatives would be selected.How much slack is there in the third constraint?
A)0
B)3
C)33
D)36
E)None of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
39
A type of integer programming is
A)pure.
B)mixed.
C)zero-one.
D)All of the above
E)None of the above
A)pure.
B)mixed.
C)zero-one.
D)All of the above
E)None of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
40
Assignment problems solved previously by linear programming techniques are also examples of
A)pure-integer programming problems.
B)mixed-integer programming problems.
C)zero-one integer programming problems.
D)goal programming problems.
E)nonlinear programming problems.
A)pure-integer programming problems.
B)mixed-integer programming problems.
C)zero-one integer programming problems.
D)goal programming problems.
E)nonlinear programming problems.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
41
The concept of "satisficing" is affiliated with which of the following?
A)mixed integer programming
B)integer programming
C)linear programming
D)nonlinear programming
E)goal programming
A)mixed integer programming
B)integer programming
C)linear programming
D)nonlinear programming
E)goal programming

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
42
The overall best solution in a nonlinear program is a
A)global optimum.
B)local optimum.
C)binary optimum.
D)nonlinear optimum.
E)goal optimum.
A)global optimum.
B)local optimum.
C)binary optimum.
D)nonlinear optimum.
E)goal optimum.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
43
A goal programming problem had two goals (with no priorities assigned).Goal number 1 was to achieve a cost of $2,400 and goal number 2 was to have no idle time for workers in the factory.The optimal solution to this problem resulted in a cost of $2,400 and no idle time.What was the value for the objective function for this goal programming problem?
A)2300
B)100
C)-100
D)0
E)None of the above
A)2300
B)100
C)-100
D)0
E)None of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
44
The concept of a local optimum is affiliated with which of the following?
A)mixed integer programming
B)integer programming
C)linear programming
D)nonlinear programming
E)goal programming
A)mixed integer programming
B)integer programming
C)linear programming
D)nonlinear programming
E)goal programming

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
45
An integer programming (maximization)problem was first solved as a linear programming problem,and the objective function value (profit)was $253.67.The two decision variables (X,Y)in the problem had values of X = 12.45 and Y = 32.75.Which of the following must be true for the optimal integer solution to this problem?
A)X = 12 Y = 32
B)X = 12 Y = 33
C)X = 12
D)Y = 32
E)None of the above
A)X = 12 Y = 32
B)X = 12 Y = 33
C)X = 12
D)Y = 32
E)None of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
46
Which of the following is not considered nonlinear programming?
A)nonlinear objective and nonlinear constraints
B)linear objective with nonlinear constraints
C)nonlinear objective with linear constraints
D)binary decision variable with nonlinear constraints
E)integer decision variable with linear constraints
A)nonlinear objective and nonlinear constraints
B)linear objective with nonlinear constraints
C)nonlinear objective with linear constraints
D)binary decision variable with nonlinear constraints
E)integer decision variable with linear constraints

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
47
A transportation problem is an example of
A)a pure-integer programming problem.
B)a mixed-integer programming problem.
C)a zero-one integer programming problem.
D)a goal programming problem.
E)a nonlinear programming problem.
A)a pure-integer programming problem.
B)a mixed-integer programming problem.
C)a zero-one integer programming problem.
D)a goal programming problem.
E)a nonlinear programming problem.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
48
Another name for a 0-1 variable is a(n)________ variable.
A)either-or
B)binary
C)yes-no
D)quadratic
E)on-off
A)either-or
B)binary
C)yes-no
D)quadratic
E)on-off

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
49
A quadratic programming problem involves which of the following conditions?
A)squared terms in the objective function and linear constraints
B)linear objective function and squared terms in the constraints
C)squared terms in both the objective function and constraints
D)a strictly goal programming problem with squared terms in the objective function
E)None of the above
A)squared terms in the objective function and linear constraints
B)linear objective function and squared terms in the constraints
C)squared terms in both the objective function and constraints
D)a strictly goal programming problem with squared terms in the objective function
E)None of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
50
If we wish to develop a stock portfolio wherein we maximize return and minimize risk,we would have to use
A)pure-integer programming.
B)goal programming.
C)zero-one integer programming.
D)mixed-integer programming.
E)nonlinear programming.
A)pure-integer programming.
B)goal programming.
C)zero-one integer programming.
D)mixed-integer programming.
E)nonlinear programming.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
51
As part of a larger problem,you are trying to determine whether or not to open a plant with a capacity of 10,000 units (using binary variable Y).You also define X as the number of units (if any)produced at that plant.How will you ensure that Y will equal 1 if the plant is open?
A)Y ≥ X
B)Y ≤ X
C)X + Y ≥ 2
D)X = 10000Y
E)X ≤ 10000Y
A)Y ≥ X
B)Y ≤ X
C)X + Y ≥ 2
D)X = 10000Y
E)X ≤ 10000Y

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
52
A capital budgeting problem involving the selection of possible projects under budget constraints is solved by which of the following?
A)mixed-integer programming
B)0-1 integer programming
C)goal programming
D)nonlinear programming
E)pure integer programming
A)mixed-integer programming
B)0-1 integer programming
C)goal programming
D)nonlinear programming
E)pure integer programming

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
53
Table 10-3
A company has decided to use 0−1 integer programming to help make some investment decisions.There are three possible investment alternatives from which to choose,but if it is decided that a particular alternative is to be selected,the entire cost of that alternative will be incurred (i.e. ,it is impossible to build one-half of a factory).The integer programming model is as follows:
Maximize 5000 X1 + 7000X2 + 9000X3
Subject to: X1 + X2 + X3 ≤ 2 Constraint 1
-X1 + X2 ≤ 0 Constraint 2
25,000 X1 + 32,000 X2 + 29,000 X3 ≤ 62,000 (budget limit)
16 X1 + 14 X2 + 19 X3 ≤ 36 (resource limitation)
all variables = 0 or 1
where X1 = 1 if alternative 1 is selected,0 otherwise
X2 = 1 if alternative 2 is selected,0 otherwise
X3 = 1 if alternative 3 is selected,0 otherwise
Solution x1 = 1,x2 = 0,x3 = 1,objective value = 14,000.
Table 10-3 presents an integer programming problem.What is the meaning of Constraint 2?
A)Both alternatives 1 and 2 must be selected.
B)If alternative 2 is selected,alternative 1 must also be selected.
C)Either alternative 1 or alternative 2 must be selected.
D)No more than one alternative may be selected.
E)None of the above
A company has decided to use 0−1 integer programming to help make some investment decisions.There are three possible investment alternatives from which to choose,but if it is decided that a particular alternative is to be selected,the entire cost of that alternative will be incurred (i.e. ,it is impossible to build one-half of a factory).The integer programming model is as follows:
Maximize 5000 X1 + 7000X2 + 9000X3
Subject to: X1 + X2 + X3 ≤ 2 Constraint 1
-X1 + X2 ≤ 0 Constraint 2
25,000 X1 + 32,000 X2 + 29,000 X3 ≤ 62,000 (budget limit)
16 X1 + 14 X2 + 19 X3 ≤ 36 (resource limitation)
all variables = 0 or 1
where X1 = 1 if alternative 1 is selected,0 otherwise
X2 = 1 if alternative 2 is selected,0 otherwise
X3 = 1 if alternative 3 is selected,0 otherwise
Solution x1 = 1,x2 = 0,x3 = 1,objective value = 14,000.
Table 10-3 presents an integer programming problem.What is the meaning of Constraint 2?
A)Both alternatives 1 and 2 must be selected.
B)If alternative 2 is selected,alternative 1 must also be selected.
C)Either alternative 1 or alternative 2 must be selected.
D)No more than one alternative may be selected.
E)None of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
54
Which of the following statements is false concerning goal programming?
A)The objective function is the main difference between linear programming and goal programming.
B)The objective in goal programming is to minimize deviational variables.
C)Deviational variables are zero if a goal is completely obtained.
D)It is not possible for two goals to have equal priority.
E)The priorities of each goal are reflected in the objective function.
A)The objective function is the main difference between linear programming and goal programming.
B)The objective in goal programming is to minimize deviational variables.
C)Deviational variables are zero if a goal is completely obtained.
D)It is not possible for two goals to have equal priority.
E)The priorities of each goal are reflected in the objective function.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
55
A goal programming problem had two goals (with no priorities assigned).Goal number 1 was to achieve a cost of $3,600 and goal number 2 was to have no wasted material.The optimal solution to this problem resulted in a cost of $3,900 and no wasted material.What was the value for the objective function for this goal programming problem?
A)300
B)-300
C)3300
D)0
E)None of the above
A)300
B)-300
C)3300
D)0
E)None of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
56
Table 10-3
A company has decided to use 0−1 integer programming to help make some investment decisions.There are three possible investment alternatives from which to choose,but if it is decided that a particular alternative is to be selected,the entire cost of that alternative will be incurred (i.e. ,it is impossible to build one-half of a factory).The integer programming model is as follows:
Maximize 5000 X1 + 7000X2 + 9000X3
Subject to: X1 + X2 + X3 ≤ 2 Constraint 1
-X1 + X2 ≤ 0 Constraint 2
25,000 X1 + 32,000 X2 + 29,000 X3 ≤ 62,000 (budget limit)
16 X1 + 14 X2 + 19 X3 ≤ 36 (resource limitation)
all variables = 0 or 1
where X1 = 1 if alternative 1 is selected,0 otherwise
X2 = 1 if alternative 2 is selected,0 otherwise
X3 = 1 if alternative 3 is selected,0 otherwise
Solution x1 = 1,x2 = 0,x3 = 1,objective value = 14,000.
Table 10-3 presents an integer programming problem.What is the meaning of Constraint 1?
A)If X1 is selected,X2 must also be selected.
B)No more than two alternatives may be selected.
C)At least two alternatives must be selected.
D)If X2 is selected,X1 must also be selected.
E)None of the above
A company has decided to use 0−1 integer programming to help make some investment decisions.There are three possible investment alternatives from which to choose,but if it is decided that a particular alternative is to be selected,the entire cost of that alternative will be incurred (i.e. ,it is impossible to build one-half of a factory).The integer programming model is as follows:
Maximize 5000 X1 + 7000X2 + 9000X3
Subject to: X1 + X2 + X3 ≤ 2 Constraint 1
-X1 + X2 ≤ 0 Constraint 2
25,000 X1 + 32,000 X2 + 29,000 X3 ≤ 62,000 (budget limit)
16 X1 + 14 X2 + 19 X3 ≤ 36 (resource limitation)
all variables = 0 or 1
where X1 = 1 if alternative 1 is selected,0 otherwise
X2 = 1 if alternative 2 is selected,0 otherwise
X3 = 1 if alternative 3 is selected,0 otherwise
Solution x1 = 1,x2 = 0,x3 = 1,objective value = 14,000.
Table 10-3 presents an integer programming problem.What is the meaning of Constraint 1?
A)If X1 is selected,X2 must also be selected.
B)No more than two alternatives may be selected.
C)At least two alternatives must be selected.
D)If X2 is selected,X1 must also be selected.
E)None of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
57
Terms that are minimized in goal programming are called
A)deviational variables.
B)global variables.
C)decision variables.
D)minimization variables.
E)None of the above
A)deviational variables.
B)global variables.
C)decision variables.
D)minimization variables.
E)None of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
58
Consider the following 0-1 integer programming problem:  If we wish to add the constraint that no more than two of these variables must be positive,how would this be written?
If we wish to add the constraint that no more than two of these variables must be positive,how would this be written?
A)2X + 2Y + 2Z ≤ 3
B)X + Y + Z ≤ 2
C)X ≤ 2,and Y ≤ 2,and Z ≤ 2
D)X,Y,Z ≤ 2
E)None of the above
 If we wish to add the constraint that no more than two of these variables must be positive,how would this be written?
If we wish to add the constraint that no more than two of these variables must be positive,how would this be written?A)2X + 2Y + 2Z ≤ 3
B)X + Y + Z ≤ 2
C)X ≤ 2,and Y ≤ 2,and Z ≤ 2
D)X,Y,Z ≤ 2
E)None of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
59
The following  represents a:
represents a:
A)goal programming problem.
B)mixed integer programming problem.
C)nonlinear programming problem.
D)0-1 integer programming problem.
E)pure integer programming problem.
 represents a:
represents a:A)goal programming problem.
B)mixed integer programming problem.
C)nonlinear programming problem.
D)0-1 integer programming problem.
E)pure integer programming problem.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
60
Consider the following 0 - 1 integer programming problem:  If we wish to add the constraint that X must be positive,and that only Y or Z,but not both,can be positive,how would the additional constraint(s)be written?
If we wish to add the constraint that X must be positive,and that only Y or Z,but not both,can be positive,how would the additional constraint(s)be written?
A)X + Y + Z ≤ 3,Y + Z ≤ 1
B)X ≤ 1,Y + Z = 1
C)X ≤ 2,and Y ≤ 2,and Z ≤ 2
D)X = 1,Y + Z ≤ 1
E)None of the above
 If we wish to add the constraint that X must be positive,and that only Y or Z,but not both,can be positive,how would the additional constraint(s)be written?
If we wish to add the constraint that X must be positive,and that only Y or Z,but not both,can be positive,how would the additional constraint(s)be written?A)X + Y + Z ≤ 3,Y + Z ≤ 1
B)X ≤ 1,Y + Z = 1
C)X ≤ 2,and Y ≤ 2,and Z ≤ 2
D)X = 1,Y + Z ≤ 1
E)None of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
61
Table 10-5
Maximize Z = 34 X1 + 43 X2 + 29 X3
Subject to: 5 X1 + 4 X2 + 7 X3 ≤ 50
1 X1 + 2 X2 + 2 X3 ≤ 16
3 X1 + 4 X2 + 1 X3 ≤ 9
all Xi are integer and non-negative
Final Integer Solution: Z = 208
Decision
Variable Solution
X1 1
X2 0
X3 6
Table 10-5 represents a solution for an integer programming problem.If this problem had been solved as a simple linear programming problem,what would you expect the value of the objective function to be?
A)less than 208
B)greater than 208
C)exactly 208
D)A or C
E)B or C
Maximize Z = 34 X1 + 43 X2 + 29 X3
Subject to: 5 X1 + 4 X2 + 7 X3 ≤ 50
1 X1 + 2 X2 + 2 X3 ≤ 16
3 X1 + 4 X2 + 1 X3 ≤ 9
all Xi are integer and non-negative
Final Integer Solution: Z = 208
Decision
Variable Solution
X1 1
X2 0
X3 6
Table 10-5 represents a solution for an integer programming problem.If this problem had been solved as a simple linear programming problem,what would you expect the value of the objective function to be?
A)less than 208
B)greater than 208
C)exactly 208
D)A or C
E)B or C

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
62
Table 10-7
The Elastic Firm has two products coming on the market: Zigs and Zags.To make a Zig,the firm needs 10 units of product A and 15 units of product B.To make a Zag,they need 20 units of product A and 30 units of product B.There are only 2,000 units of product A and 3,200 units of product B available to the firm.The profit on a Zig is $4 and on a Zag it is $6.Management objectives in order of their priority are:
(1)Produce exactly 50 Zigs.
(2)Achieve a target profit of at least $750.
(3)Use all of the product B available.
Let X1 = number of Zigs,X2 = number of Zags.
d1- = underachievement of Zig goal
d1+ = overachievement of Zig goal
d2- = underachievement of profit target
d2+ = overachievement of profit target
d3- = unused product B
d3+ = additional amount of product B needed
In the goal programming problem described in Table 10-7,what is the optimal solution?
A)X1 = 75 + X2 = 91.67
B)X1 = 91.67 + X2 = 50
C)X1 = 50 + X2 = 75
D)X1 = 50 + X2 = 91.67
E)X1 = 75 + X2 = 50
The Elastic Firm has two products coming on the market: Zigs and Zags.To make a Zig,the firm needs 10 units of product A and 15 units of product B.To make a Zag,they need 20 units of product A and 30 units of product B.There are only 2,000 units of product A and 3,200 units of product B available to the firm.The profit on a Zig is $4 and on a Zag it is $6.Management objectives in order of their priority are:
(1)Produce exactly 50 Zigs.
(2)Achieve a target profit of at least $750.
(3)Use all of the product B available.
Let X1 = number of Zigs,X2 = number of Zags.
d1- = underachievement of Zig goal
d1+ = overachievement of Zig goal
d2- = underachievement of profit target
d2+ = overachievement of profit target
d3- = unused product B
d3+ = additional amount of product B needed
In the goal programming problem described in Table 10-7,what is the optimal solution?
A)X1 = 75 + X2 = 91.67
B)X1 = 91.67 + X2 = 50
C)X1 = 50 + X2 = 75
D)X1 = 50 + X2 = 91.67
E)X1 = 75 + X2 = 50

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
63
Agile Bikes has manufacturing plants in Salt Lake City,Dallas,and Chicago.The bikes are shipped to retail stores in Los Angeles,New York,Miami,and Seattle.Information on shipping costs,supply,and demand is given in the following table:  What type of mathematical programming is required to solve this problem?
What type of mathematical programming is required to solve this problem?
A)Linear programming
B)Integer programming
C)Mixed-integer programming
D)Zero-one integer programming
E)Nonlinear programming
 What type of mathematical programming is required to solve this problem?
What type of mathematical programming is required to solve this problem?A)Linear programming
B)Integer programming
C)Mixed-integer programming
D)Zero-one integer programming
E)Nonlinear programming

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
64
A model containing a linear objective function and requiring that one or more of the decision variables take on an integer value in the final solution is called
A)an integer programming problem.
B)a goal programming problem.
C)a nonlinear programming problem.
D)a multiple objective LP problem.
E)insufficient information.
A)an integer programming problem.
B)a goal programming problem.
C)a nonlinear programming problem.
D)a multiple objective LP problem.
E)insufficient information.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
65
Table 10-3
A company has decided to use 0−1 integer programming to help make some investment decisions.There are three possible investment alternatives from which to choose,but if it is decided that a particular alternative is to be selected,the entire cost of that alternative will be incurred (i.e. ,it is impossible to build one-half of a factory).The integer programming model is as follows:
Maximize 5000 X1 + 7000X2 + 9000X3
Subject to: X1 + X2 + X3 ≤ 2 Constraint 1
-X1 + X2 ≤ 0 Constraint 2
25,000 X1 + 32,000 X2 + 29,000 X3 ≤ 62,000 (budget limit)
16 X1 + 14 X2 + 19 X3 ≤ 36 (resource limitation)
all variables = 0 or 1
where X1 = 1 if alternative 1 is selected,0 otherwise
X2 = 1 if alternative 2 is selected,0 otherwise
X3 = 1 if alternative 3 is selected,0 otherwise
Solution x1 = 1,x2 = 0,x3 = 1,objective value = 14,000.
Table 10-3 presents an integer programming problem.If the optimal solution is used,then only two of the alternatives would be selected.How much slack would there be in the third constraint?
A)1000
B)5000
C)3300
D)8000
E)None of the above
A company has decided to use 0−1 integer programming to help make some investment decisions.There are three possible investment alternatives from which to choose,but if it is decided that a particular alternative is to be selected,the entire cost of that alternative will be incurred (i.e. ,it is impossible to build one-half of a factory).The integer programming model is as follows:
Maximize 5000 X1 + 7000X2 + 9000X3
Subject to: X1 + X2 + X3 ≤ 2 Constraint 1
-X1 + X2 ≤ 0 Constraint 2
25,000 X1 + 32,000 X2 + 29,000 X3 ≤ 62,000 (budget limit)
16 X1 + 14 X2 + 19 X3 ≤ 36 (resource limitation)
all variables = 0 or 1
where X1 = 1 if alternative 1 is selected,0 otherwise
X2 = 1 if alternative 2 is selected,0 otherwise
X3 = 1 if alternative 3 is selected,0 otherwise
Solution x1 = 1,x2 = 0,x3 = 1,objective value = 14,000.
Table 10-3 presents an integer programming problem.If the optimal solution is used,then only two of the alternatives would be selected.How much slack would there be in the third constraint?
A)1000
B)5000
C)3300
D)8000
E)None of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
66
Table 10-7
The Elastic Firm has two products coming on the market: Zigs and Zags.To make a Zig,the firm needs 10 units of product A and 15 units of product B.To make a Zag,they need 20 units of product A and 30 units of product B.There are only 2,000 units of product A and 3,200 units of product B available to the firm.The profit on a Zig is $4 and on a Zag it is $6.Management objectives in order of their priority are:
(1)Produce exactly 50 Zigs.
(2)Achieve a target profit of at least $750.
(3)Use all of the product B available.
Let X1 = number of Zigs,X2 = number of Zags.
d1- = underachievement of Zig goal
d1+ = overachievement of Zig goal
d2- = underachievement of profit target
d2+ = overachievement of profit target
d3- = unused product B
d3+ = additional amount of product B needed
In the goal programming problem described in Table 10-7,how is the goal of achieving a target profit of at least $750 expressed?
A)X1 + X2 + d2- = 750
B)X1 + X2 + d2- - d2+ = 750
C)4X1 +6 X2 + d2- = 750
D)4X1 + 6X2 + d2- - d2+ = 750
E)X1 + X2 - d2+ = 750
The Elastic Firm has two products coming on the market: Zigs and Zags.To make a Zig,the firm needs 10 units of product A and 15 units of product B.To make a Zag,they need 20 units of product A and 30 units of product B.There are only 2,000 units of product A and 3,200 units of product B available to the firm.The profit on a Zig is $4 and on a Zag it is $6.Management objectives in order of their priority are:
(1)Produce exactly 50 Zigs.
(2)Achieve a target profit of at least $750.
(3)Use all of the product B available.
Let X1 = number of Zigs,X2 = number of Zags.
d1- = underachievement of Zig goal
d1+ = overachievement of Zig goal
d2- = underachievement of profit target
d2+ = overachievement of profit target
d3- = unused product B
d3+ = additional amount of product B needed
In the goal programming problem described in Table 10-7,how is the goal of achieving a target profit of at least $750 expressed?
A)X1 + X2 + d2- = 750
B)X1 + X2 + d2- - d2+ = 750
C)4X1 +6 X2 + d2- = 750
D)4X1 + 6X2 + d2- - d2+ = 750
E)X1 + X2 - d2+ = 750

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
67
Table 10-4 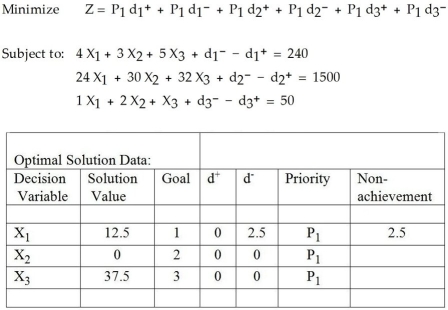
Table 10-4 represents a solution to a goal programming problem.There are three goals (each represented by a constraint).Which goals are only partly achieved?
A)number 1 only
B)number 1 and number 2
C)number 2 and number 3
D)number 1 and number 3
E)None of the above

Table 10-4 represents a solution to a goal programming problem.There are three goals (each represented by a constraint).Which goals are only partly achieved?
A)number 1 only
B)number 1 and number 2
C)number 2 and number 3
D)number 1 and number 3
E)None of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
68
Table 10-4 
Table 10-4 represents a solution to a goal programming problem.There are three goals (each represented by a constraint).Which of the goals is assigned the highest priority?
A)goal 1
B)goal 2
C)goal 3
D)goals 2 and 3
E)All goals have the same priority.

Table 10-4 represents a solution to a goal programming problem.There are three goals (each represented by a constraint).Which of the goals is assigned the highest priority?
A)goal 1
B)goal 2
C)goal 3
D)goals 2 and 3
E)All goals have the same priority.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
69
Table 10-3
A company has decided to use 0−1 integer programming to help make some investment decisions.There are three possible investment alternatives from which to choose,but if it is decided that a particular alternative is to be selected,the entire cost of that alternative will be incurred (i.e. ,it is impossible to build one-half of a factory).The integer programming model is as follows:
Maximize 5000 X1 + 7000X2 + 9000X3
Subject to: X1 + X2 + X3 ≤ 2 Constraint 1
-X1 + X2 ≤ 0 Constraint 2
25,000 X1 + 32,000 X2 + 29,000 X3 ≤ 62,000 (budget limit)
16 X1 + 14 X2 + 19 X3 ≤ 36 (resource limitation)
all variables = 0 or 1
where X1 = 1 if alternative 1 is selected,0 otherwise
X2 = 1 if alternative 2 is selected,0 otherwise
X3 = 1 if alternative 3 is selected,0 otherwise
Solution x1 = 1,x2 = 0,x3 = 1,objective value = 14,000.
Table 10-3 presents an integer programming problem.Suppose you wish to add a constraint that stipulates that both alternative 2 and alternative 3 must be selected,or neither can be selected.How would this constraint be written?
A)X2 = X3
B)X2 ≤ X3
C)X2 ≥ X3
D)X2 + X3 = 1
E)None of the above
A company has decided to use 0−1 integer programming to help make some investment decisions.There are three possible investment alternatives from which to choose,but if it is decided that a particular alternative is to be selected,the entire cost of that alternative will be incurred (i.e. ,it is impossible to build one-half of a factory).The integer programming model is as follows:
Maximize 5000 X1 + 7000X2 + 9000X3
Subject to: X1 + X2 + X3 ≤ 2 Constraint 1
-X1 + X2 ≤ 0 Constraint 2
25,000 X1 + 32,000 X2 + 29,000 X3 ≤ 62,000 (budget limit)
16 X1 + 14 X2 + 19 X3 ≤ 36 (resource limitation)
all variables = 0 or 1
where X1 = 1 if alternative 1 is selected,0 otherwise
X2 = 1 if alternative 2 is selected,0 otherwise
X3 = 1 if alternative 3 is selected,0 otherwise
Solution x1 = 1,x2 = 0,x3 = 1,objective value = 14,000.
Table 10-3 presents an integer programming problem.Suppose you wish to add a constraint that stipulates that both alternative 2 and alternative 3 must be selected,or neither can be selected.How would this constraint be written?
A)X2 = X3
B)X2 ≤ X3
C)X2 ≥ X3
D)X2 + X3 = 1
E)None of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
70
Table 10-6
The profit function for a set of two electronics products can be expressed by the following expression: X12 -2X1 -3X2 + 2X22 where X1 = the number of product 1 units produced and X2 = the number of product 2 units produced.At least 10 units of X1 must be produced and at least 20 units of X2 must be produced.No more than 50 units total can be produced.
What type of mathematical programming model is required for the problem described in Table 10-6?
A)An integer programming model
B)A goal programming model
C)A nonlinear programming model
D)A zero-one integer programming model
E)A mixed-integer programming model
The profit function for a set of two electronics products can be expressed by the following expression: X12 -2X1 -3X2 + 2X22 where X1 = the number of product 1 units produced and X2 = the number of product 2 units produced.At least 10 units of X1 must be produced and at least 20 units of X2 must be produced.No more than 50 units total can be produced.
What type of mathematical programming model is required for the problem described in Table 10-6?
A)An integer programming model
B)A goal programming model
C)A nonlinear programming model
D)A zero-one integer programming model
E)A mixed-integer programming model

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
71
What is the optimal solution to the problem described in Table 10-6?
A)X1 = 50;X2 = 0
B)X1 = 30;X2 = 20
C)X1 = 20;X2 = 30
D)X1 = 25;X2 = 25
E)X1 = 0;X2 = 25
A)X1 = 50;X2 = 0
B)X1 = 30;X2 = 20
C)X1 = 20;X2 = 30
D)X1 = 25;X2 = 25
E)X1 = 0;X2 = 25

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
72
Table 10-7
The Elastic Firm has two products coming on the market: Zigs and Zags.To make a Zig,the firm needs 10 units of product A and 15 units of product B.To make a Zag,they need 20 units of product A and 30 units of product B.There are only 2,000 units of product A and 3,200 units of product B available to the firm.The profit on a Zig is $4 and on a Zag it is $6.Management objectives in order of their priority are:
(1)Produce exactly 50 Zigs.
(2)Achieve a target profit of at least $750.
(3)Use all of the product B available.
Let X1 = number of Zigs,X2 = number of Zags.
d1- = underachievement of Zig goal
d1+ = overachievement of Zig goal
d2- = underachievement of profit target
d2+ = overachievement of profit target
d3- = unused product B
d3+ = additional amount of product B needed
In the goal programming problem described in Table 10-7,what is the objective function?
A)Min: P1d1- + P1d1+ + P2d2+ + P2d2- + P3d3- + P3d3+
B)Min: P1d1- + P1d1+ + P2d2+ + P3d3+
C)Min: P1d1- + P1d1+ + P2d2- + P3d3-
D)Min: P1d1- + P2d2- + P3d3-
E)Min: P1d1+ + P2d2+ + P3d3+
The Elastic Firm has two products coming on the market: Zigs and Zags.To make a Zig,the firm needs 10 units of product A and 15 units of product B.To make a Zag,they need 20 units of product A and 30 units of product B.There are only 2,000 units of product A and 3,200 units of product B available to the firm.The profit on a Zig is $4 and on a Zag it is $6.Management objectives in order of their priority are:
(1)Produce exactly 50 Zigs.
(2)Achieve a target profit of at least $750.
(3)Use all of the product B available.
Let X1 = number of Zigs,X2 = number of Zags.
d1- = underachievement of Zig goal
d1+ = overachievement of Zig goal
d2- = underachievement of profit target
d2+ = overachievement of profit target
d3- = unused product B
d3+ = additional amount of product B needed
In the goal programming problem described in Table 10-7,what is the objective function?
A)Min: P1d1- + P1d1+ + P2d2+ + P2d2- + P3d3- + P3d3+
B)Min: P1d1- + P1d1+ + P2d2+ + P3d3+
C)Min: P1d1- + P1d1+ + P2d2- + P3d3-
D)Min: P1d1- + P2d2- + P3d3-
E)Min: P1d1+ + P2d2+ + P3d3+

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
73
Table 10-7
The Elastic Firm has two products coming on the market: Zigs and Zags.To make a Zig,the firm needs 10 units of product A and 15 units of product B.To make a Zag,they need 20 units of product A and 30 units of product B.There are only 2,000 units of product A and 3,200 units of product B available to the firm.The profit on a Zig is $4 and on a Zag it is $6.Management objectives in order of their priority are:
(1)Produce exactly 50 Zigs.
(2)Achieve a target profit of at least $750.
(3)Use all of the product B available.
Let X1 = number of Zigs,X2 = number of Zags.
d1- = underachievement of Zig goal
d1+ = overachievement of Zig goal
d2- = underachievement of profit target
d2+ = overachievement of profit target
d3- = unused product B
d3+ = additional amount of product B needed
In the goal programming problem described in Table 10-7,how is the goal of producing exactly 50 Zigs expressed?
A)X1 + d1+ = 50
B)X1 - d1+ = 50
C)X1 + d1- = 50
D)X1 - d1- = 50
E)X1 + d1- - d1+ = 50
The Elastic Firm has two products coming on the market: Zigs and Zags.To make a Zig,the firm needs 10 units of product A and 15 units of product B.To make a Zag,they need 20 units of product A and 30 units of product B.There are only 2,000 units of product A and 3,200 units of product B available to the firm.The profit on a Zig is $4 and on a Zag it is $6.Management objectives in order of their priority are:
(1)Produce exactly 50 Zigs.
(2)Achieve a target profit of at least $750.
(3)Use all of the product B available.
Let X1 = number of Zigs,X2 = number of Zags.
d1- = underachievement of Zig goal
d1+ = overachievement of Zig goal
d2- = underachievement of profit target
d2+ = overachievement of profit target
d3- = unused product B
d3+ = additional amount of product B needed
In the goal programming problem described in Table 10-7,how is the goal of producing exactly 50 Zigs expressed?
A)X1 + d1+ = 50
B)X1 - d1+ = 50
C)X1 + d1- = 50
D)X1 - d1- = 50
E)X1 + d1- - d1+ = 50

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
74
According to Table 10-6,how is the constraint expressed that no more than 50 units can be produced?
A)X1 + X2 ≥ 50
B)X1 + X2 ≤ 50
C)X12 + X22 ≥ 50
D)X12 + X22 ≤ 50
E)X1 + X2 = 50
A)X1 + X2 ≥ 50
B)X1 + X2 ≤ 50
C)X12 + X22 ≥ 50
D)X12 + X22 ≤ 50
E)X1 + X2 = 50

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
75
Table 10-4 
Table 10-4 represents a solution to a goal programming problem.There are three goals (each represented by a constraint).Goal number 3 represents a resource usage goal.How much of this resource would be used by this solution?
A)50 units
B)70 units
C)2500 units
D)240 units
E)None of the above

Table 10-4 represents a solution to a goal programming problem.There are three goals (each represented by a constraint).Goal number 3 represents a resource usage goal.How much of this resource would be used by this solution?
A)50 units
B)70 units
C)2500 units
D)240 units
E)None of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
76
Goal programming and linear programming differ in that
A)in LP,the objective function is maximized or minimized,while in goal programming,the deviation between goals and possible achievement is minimized.
B)slack variables are used in LP,while deviational variables are used in goal programming.
C)deviational variables have positive objective function coefficients in goal programming,but slack variables have 0 coefficients in LP.
D)All of the above
E)None of the above
A)in LP,the objective function is maximized or minimized,while in goal programming,the deviation between goals and possible achievement is minimized.
B)slack variables are used in LP,while deviational variables are used in goal programming.
C)deviational variables have positive objective function coefficients in goal programming,but slack variables have 0 coefficients in LP.
D)All of the above
E)None of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
77
Classify the following problems as to whether they are pure-integer,mixed-integer,zero-one,goal,or nonlinear programming problems.
(a)Maximize Z = 5 X1 + 6 X1 X2 + 2 X2
Subject to: 3 X1 + 2 X2 ≥ 6
X1 + X2 ≤ 8
X1,X2 ≥ 0
(b)Minimize Z = 8 X1 + 6 X2
Subject to: 4 X1 + 5 X2 ≥ 10
X1 + X2 ≤ 3
X1,X2 ≥ 0
X1,X2 = 0 or 1
(c)Maximize Z = 10 X1 + 5 X2
Subject to: 8 X1 + 10 X2 = 10
4 X1 + 6 X2 ≥ 5
X1,X2 integer
(d)Minimize Z = 8 X12 + 4 X1 X2 + 12 X22
Subject to: 6 X1 + X2 ≥ 50
X1 + X2 ≥ 40
(a)Maximize Z = 5 X1 + 6 X1 X2 + 2 X2
Subject to: 3 X1 + 2 X2 ≥ 6
X1 + X2 ≤ 8
X1,X2 ≥ 0
(b)Minimize Z = 8 X1 + 6 X2
Subject to: 4 X1 + 5 X2 ≥ 10
X1 + X2 ≤ 3
X1,X2 ≥ 0
X1,X2 = 0 or 1
(c)Maximize Z = 10 X1 + 5 X2
Subject to: 8 X1 + 10 X2 = 10
4 X1 + 6 X2 ≥ 5
X1,X2 integer
(d)Minimize Z = 8 X12 + 4 X1 X2 + 12 X22
Subject to: 6 X1 + X2 ≥ 50
X1 + X2 ≥ 40

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
78
A goal programming problem had two goals (with no priorities assigned).Goal number 1 was to achieve a cost of $3,600 and goal number 2 was to complete the task in 400 hours or fewer.The optimal solution to this problem resulted in a cost of $3,600 and a completion time of 420 hours.What was the value for the objective function for this goal programming problem?
A)400
B)-400
C)20
D)0
E)None of the above
A)400
B)-400
C)20
D)0
E)None of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
79
Table 10-5
Maximize Z = 34 X1 + 43 X2 + 29 X3
Subject to: 5 X1 + 4 X2 + 7 X3 ≤ 50
1 X1 + 2 X2 + 2 X3 ≤ 16
3 X1 + 4 X2 + 1 X3 ≤ 9
all Xi are integer and non-negative
Final Integer Solution: Z = 208
Decision
Variable Solution
X1 1
X2 0
X3 6
Table 10-5 represents a solution for an integer programming problem.If one uses the optimal solution presented,how much slack is there in the first equation?
A)0 units
B)5 units
C)3 units
D)2 units
E)None of the above
Maximize Z = 34 X1 + 43 X2 + 29 X3
Subject to: 5 X1 + 4 X2 + 7 X3 ≤ 50
1 X1 + 2 X2 + 2 X3 ≤ 16
3 X1 + 4 X2 + 1 X3 ≤ 9
all Xi are integer and non-negative
Final Integer Solution: Z = 208
Decision
Variable Solution
X1 1
X2 0
X3 6
Table 10-5 represents a solution for an integer programming problem.If one uses the optimal solution presented,how much slack is there in the first equation?
A)0 units
B)5 units
C)3 units
D)2 units
E)None of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
80
Table 10-7
The Elastic Firm has two products coming on the market: Zigs and Zags.To make a Zig,the firm needs 10 units of product A and 15 units of product B.To make a Zag,they need 20 units of product A and 30 units of product B.There are only 2,000 units of product A and 3,200 units of product B available to the firm.The profit on a Zig is $4 and on a Zag it is $6.Management objectives in order of their priority are:
(1)Produce exactly 50 Zigs.
(2)Achieve a target profit of at least $750.
(3)Use all of the product B available.
Let X1 = number of Zigs,X2 = number of Zags.
d1- = underachievement of Zig goal
d1+ = overachievement of Zig goal
d2- = underachievement of profit target
d2+ = overachievement of profit target
d3- = unused product B
d3+ = additional amount of product B needed
In the goal programming problem described in Table 10-7,how is the goal of the use of all product B available expressed?
A)15X1 + 30X2 + d3- - d3+ = 3200
B)X1 + X2 + d3- - d3+ = 3200
C)X1 + X2 + d3- = 3200
D)15X1 + 30X2 + d3- = 3200
E)15X1 + 3-X2 - d3+ = 3200
The Elastic Firm has two products coming on the market: Zigs and Zags.To make a Zig,the firm needs 10 units of product A and 15 units of product B.To make a Zag,they need 20 units of product A and 30 units of product B.There are only 2,000 units of product A and 3,200 units of product B available to the firm.The profit on a Zig is $4 and on a Zag it is $6.Management objectives in order of their priority are:
(1)Produce exactly 50 Zigs.
(2)Achieve a target profit of at least $750.
(3)Use all of the product B available.
Let X1 = number of Zigs,X2 = number of Zags.
d1- = underachievement of Zig goal
d1+ = overachievement of Zig goal
d2- = underachievement of profit target
d2+ = overachievement of profit target
d3- = unused product B
d3+ = additional amount of product B needed
In the goal programming problem described in Table 10-7,how is the goal of the use of all product B available expressed?
A)15X1 + 30X2 + d3- - d3+ = 3200
B)X1 + X2 + d3- - d3+ = 3200
C)X1 + X2 + d3- = 3200
D)15X1 + 30X2 + d3- = 3200
E)15X1 + 3-X2 - d3+ = 3200

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck



