Deck 3: Vectors and Motion in Two Dimensions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/180
Play
Full screen (f)
Deck 3: Vectors and Motion in Two Dimensions
1
If a vector has components Ax < 0, and Ay > 0, then the angle that this vector makes with the positive x-axis must be in the range
A)0° to 90°
B)90° to 180°
C)180° to 270°
D)270° to 360°
E)It cannot be determined without additional information.
A)0° to 90°
B)90° to 180°
C)180° to 270°
D)270° to 360°
E)It cannot be determined without additional information.
90° to 180°
2
Two displacement vectors have magnitudes of 5.0 m and 7.0 m, respectively. If these two vectors are added together, the magnitude of the sum
A)is equal to 2.0 m.
B)could be as small as 2.0 m or as large as 12 m.
C)is equal to 12 m.
D)is equal to 8.6 m.
A)is equal to 2.0 m.
B)could be as small as 2.0 m or as large as 12 m.
C)is equal to 12 m.
D)is equal to 8.6 m.
B
3
If a vector has components Ax > 0, and Ay < 0, then the angle that this vector makes with the positive x-axis must be in the range
A)0° to 90°
B)90° to 180°
C)180° to 270°
D)270° to 360°
E)cannot be determined without additional information
A)0° to 90°
B)90° to 180°
C)180° to 270°
D)270° to 360°
E)cannot be determined without additional information
270° to 360°
4
If + = and their magnitudes are given by A + B = C, then the vectors and are oriented
A)perpendicular relative to one other.
B)parallel to each other (in the same direction).
C)antiparallel to each other (in opposite directions).
D)It is impossible to know from the given information.
A)perpendicular relative to one other.
B)parallel to each other (in the same direction).
C)antiparallel to each other (in opposite directions).
D)It is impossible to know from the given information.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
5
The magnitude of a vector can never be less than the magnitude of any of its components.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
6
The magnitude of a vector an only zero if all of its components are zero.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
7
Vectors and obey the equation + = 0. These vectors satisfy which one of the following statements?
A)Vectors and are at right angles to each other.
B)Vectors and point in the same direction.
C)Vectors and have the same magnitudes.
D)The magnitude of is the negative of the magnitude of .
A)Vectors and are at right angles to each other.
B)Vectors and point in the same direction.
C)Vectors and have the same magnitudes.
D)The magnitude of is the negative of the magnitude of .

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
8
Two vectors, of magnitudes 20 mm and 50 mm, are added together. Which one of the following is a possible value for the magnitude of the resultant?
A)10 mm
B)20 mm
C)40 mm
D)80 mm
A)10 mm
B)20 mm
C)40 mm
D)80 mm

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
9
If a vector pointing upward has a positive magnitude, a vector pointing downward has a negative magnitude.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
10
The magnitude of the resultant of two vectors cannot be less than the magnitude of either of those two vectors.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
11
The sum of two vectors of fixed magnitudes has the greatest magnitude when the angle between these two vectors is
A)90°
B)180°
C)60°
D)0°
E)270°
A)90°
B)180°
C)60°
D)0°
E)270°

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
12
A student adds two displacement vectors that have the magnitudes of 12.0 m and 5.0 m. What is the range of possible answers for the magnitude of the resultant vector?

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
13
If a vector has components Ax < 0, and Ay < 0, then the angle that this vector makes with the positive x-axis must be in the range
A)0° to 90°
B)90° to 180°
C)180° to 270°
D)270° to 360°
E)cannot be determined without additional information
A)0° to 90°
B)90° to 180°
C)180° to 270°
D)270° to 360°
E)cannot be determined without additional information

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
14
The sum of two vectors of fixed magnitudes has its minimum magnitude when the angle between these vectors is
A)0°
B)90°
C)270°
D)180°
E)360°
A)0°
B)90°
C)270°
D)180°
E)360°

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
15
If three vectors add to zero, they must all have equal magnitudes.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
16
Consider two vectors and shown in the figure. The difference - is best illustrated by 
A.

B.

C.

D.

A)choice (a)
B)choice (b)
C)choice (c)
D)choice (d)

A.

B.

C.

D.

A)choice (a)
B)choice (b)
C)choice (c)
D)choice (d)

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
17
If - = 0, then the vectors and have equal magnitudes and are directed in the same direction.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
18
Consider two vectors and shown in the figure. The difference - is best illustrated by 
A.
B.
C.

D.

A)choice (a)
B)choice (b)
C)choice (c)
D)choice (d)

A.
B.

C.

D.

A)choice (a)
B)choice (b)
C)choice (c)
D)choice (d)

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
19
If a vector's components are all negative, then the magnitude of the vector is negative.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
20
The eastward component of vector is equal to the westward component of vector and their northward components are equal. Which one of the following statements must be correct for these two vectors?
A)Vector is parallel to vector .
B)Vector is antiparallel (in the opposite direction)to vector .
C)Vector must be perpendicular to vector .
D)The magnitude of vector must be equal to the magnitude of vector .
E)The angle between vector and vector must be 90°.
A)Vector is parallel to vector .
B)Vector is antiparallel (in the opposite direction)to vector .
C)Vector must be perpendicular to vector .
D)The magnitude of vector must be equal to the magnitude of vector .
E)The angle between vector and vector must be 90°.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
21
An object moves in a circular path at a constant speed. Compare the direction of the object's velocity and acceleration vectors.
A)Both vectors point in the same direction.
B)The vectors point in opposite directions.
C)The vectors are perpendicular to each other.
D)The acceleration is zero but the velocity is constant.
A)Both vectors point in the same direction.
B)The vectors point in opposite directions.
C)The vectors are perpendicular to each other.
D)The acceleration is zero but the velocity is constant.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
22
The Moon is accelerated toward the earth, so it is gradually getting closer to the earth.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
23
A boulder rolls off of a very high cliff and experiences no significant air resistance. While it is falling, its trajectory is never truly vertical.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
24
For general projectile motion with no air resistance, the vertical component of a projectile's acceleration
A)is always zero.
B)remains a non-zero constant.
C)continuously increases.
D)continuously decreases.
E)first decreases and then increases.
A)is always zero.
B)remains a non-zero constant.
C)continuously increases.
D)continuously decreases.
E)first decreases and then increases.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
25
A ball is thrown horizontally from the top of a tower at the same instant that a stone is dropped vertically. Which object is traveling faster when it hits the level ground below if neither of them experiences any air resistance?
A)It is impossible to tell because we do not know their masses.
B)the stone
C)the ball
D)Both are traveling at the same speed.
A)It is impossible to tell because we do not know their masses.
B)the stone
C)the ball
D)Both are traveling at the same speed.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
26
A pilot drops a package from a plane flying horizontally at a constant speed. Neglecting air resistance, when the package hits the ground the horizontal location of the plane will
A)be behind the package.
B)be directly over the package.
C)be in front of the package.
D)depend on the speed of the plane when the package was released.
A)be behind the package.
B)be directly over the package.
C)be in front of the package.
D)depend on the speed of the plane when the package was released.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
27
In an air-free chamber, a pebble is thrown horizontally, and at the same instant a second pebble is dropped from the same height. Compare the times of fall of the two pebbles.
A)The thrown pebble hits first.
B)The dropped pebble hits first.
C)They hit at the same time.
D)We cannot tell without knowing which pebble is heavier.
A)The thrown pebble hits first.
B)The dropped pebble hits first.
C)They hit at the same time.
D)We cannot tell without knowing which pebble is heavier.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
28
You are trying to cross a river that flows toward the south with a strong current. You start out in your motorboat on the east bank desiring to reach the west bank directly west from your starting point. You should head your motorboat
A)directly toward the west.
B)directly toward the north.
C)in a general southwesterly direction.
D)in a general northwesterly direction.
A)directly toward the west.
B)directly toward the north.
C)in a general southwesterly direction.
D)in a general northwesterly direction.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
29
If a satellite moves with constant speed in a perfectly circular orbit around the earth, what is the direction of the acceleration of the satellite?
A)in the forward direction
B)in the backward direction
C)outward away from the earth
D)inward toward the earth
E)The acceleration is zero because the speed is constant.
A)in the forward direction
B)in the backward direction
C)outward away from the earth
D)inward toward the earth
E)The acceleration is zero because the speed is constant.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
30
A velocity vector has components 36 m/s westward and 22 m/s northward. What are the magnitude and direction of this vector?

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
31
James and John dive from an overhang into the lake below. James simply drops straight down from the edge. John takes a running start and jumps with an initial horizontal velocity of 25 m/s. Compare the time it takes each to reach the lake below if there is no air resistance.
A)James reaches the surface of the lake first.
B)John reaches the surface of the lake first.
C)James and John will reach the surface of the lake at the same time.
D)Cannot be determined without knowing the mass of both James and John.
E)Cannot be determined without knowing the weight of both James and John.
A)James reaches the surface of the lake first.
B)John reaches the surface of the lake first.
C)James and John will reach the surface of the lake at the same time.
D)Cannot be determined without knowing the mass of both James and John.
E)Cannot be determined without knowing the weight of both James and John.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
32
A rock is thrown from the upper edge of a tall cliff at some angle above the horizontal. It reaches its highest point and starts falling down. Which of the following statements about the rock's motion are true just before it hits the ground? (There could be more than one correct choice.)
A)Its horizontal velocity component is zero.
B)Its velocity is vertical.
C)Its vertical velocity component is the same as it was just as it was launched.
D)Its horizontal velocity component is the same as it was just as it was launched.
E)Its speed is the same as it was just as it was launched.
A)Its horizontal velocity component is zero.
B)Its velocity is vertical.
C)Its vertical velocity component is the same as it was just as it was launched.
D)Its horizontal velocity component is the same as it was just as it was launched.
E)Its speed is the same as it was just as it was launched.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
33
Which of the following statements are true about an object in two-dimensional projectile motion with no air resistance? (There could be more than one correct choice.)
A)The speed of the object is constant but its velocity is not constant.
B)The acceleration of the object is +g when the object is rising and -g when it is falling.
C)The acceleration of the object is zero at its highest point.
D)The speed of the object is zero at its highest point.
E)The horizontal acceleration is always zero and the vertical acceleration is always a non-zero constant downward.
A)The speed of the object is constant but its velocity is not constant.
B)The acceleration of the object is +g when the object is rising and -g when it is falling.
C)The acceleration of the object is zero at its highest point.
D)The speed of the object is zero at its highest point.
E)The horizontal acceleration is always zero and the vertical acceleration is always a non-zero constant downward.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
34
For general projectile motion with no air resistance, the horizontal component of a projectile's acceleration
A)is always zero.
B)remains a non-zero constant.
C)continuously increases.
D)continuously decreases.
E)first decreases and then increases.
A)is always zero.
B)remains a non-zero constant.
C)continuously increases.
D)continuously decreases.
E)first decreases and then increases.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
35
James and John dive from an overhang into the lake below. James simply drops straight down from the edge. John takes a running start and jumps with an initial horizontal velocity of 25 m/s. If there is no air resistance, when they reach the lake below
A)the splashdown speed of James is larger than that of John.
B)the splashdown speed of John is larger than that of James.
C)they will both have the same splashdown speed.
D)the splashdown speed of James must be 9.8 m/s larger than that of John.
E)the splashdown speed of John must be 25 m/s larger than that of James.
A)the splashdown speed of James is larger than that of John.
B)the splashdown speed of John is larger than that of James.
C)they will both have the same splashdown speed.
D)the splashdown speed of James must be 9.8 m/s larger than that of John.
E)the splashdown speed of John must be 25 m/s larger than that of James.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
36
Mary and Debra stand on a snow-covered roof. They both throw snowballs with the same initial speed, but in different directions. Mary throws her snowball downward, at 30° below the horizontal; Debra throws her snowball upward, at 30° above the horizontal. Which of the following statements are true about just as the snowballs reach the ground below? (There could be more than one correct choice.)
A)Debra's snowball will have a higher speed than Mary's snowball.
B)Mary's snowball will have a higher speed than Debra's snowball.
C)Both snowballs will hit the ground with the same speed.
D)Both snowballs hit the ground at the same time.
E)Mary's snowball reaches the ground before Debra's snowball.
A)Debra's snowball will have a higher speed than Mary's snowball.
B)Mary's snowball will have a higher speed than Debra's snowball.
C)Both snowballs will hit the ground with the same speed.
D)Both snowballs hit the ground at the same time.
E)Mary's snowball reaches the ground before Debra's snowball.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
37
Vector is along the +x-axis and vector is along the +y-axis. Which one of the following statements is correct with respect to these vectors?
A)The x component of vector is equal to the x component of vector .
B)The y component of vector is equal to the y component of vector .
C)The x component of vector is equal to the y component of vector .
D)The y component of vector is equal to the x component of vector .
A)The x component of vector is equal to the x component of vector .
B)The y component of vector is equal to the y component of vector .
C)The x component of vector is equal to the y component of vector .
D)The y component of vector is equal to the x component of vector .

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
38
For general projectile motion with no air resistance, the horizontal component of a projectile's velocity
A)remains zero.
B)remains a non-zero constant.
C)continuously increases.
D)continuously decreases.
E)first decreases and then increases.
A)remains zero.
B)remains a non-zero constant.
C)continuously increases.
D)continuously decreases.
E)first decreases and then increases.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
39
Mary and Debra stand on a snow-covered roof. They both throw snowballs with the same initial speed, but in different directions. Mary throws her snowball downward, at 30° below the horizontal; Debra throws her snowball upward, at 30° above the horizontal. Which of the following statements are true about just before the snowballs reach the ground below? (There could be more than one correct choice.)
A)Debra's snowball will stay in the air longer than Mary's snowball.
B)Mary's snowball will stay in the air longer than Debra's snowball.
C)Both snowballs will take the same amount of time to hit the ground.
D)Debra's snowball has exactly the same acceleration as Mary's snowball.
E)Mary's snowball has a greater downward acceleration than Debra's snowball.
A)Debra's snowball will stay in the air longer than Mary's snowball.
B)Mary's snowball will stay in the air longer than Debra's snowball.
C)Both snowballs will take the same amount of time to hit the ground.
D)Debra's snowball has exactly the same acceleration as Mary's snowball.
E)Mary's snowball has a greater downward acceleration than Debra's snowball.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
40
A player kicks a soccer ball in a high arc toward the opponent's goal. At the highest point in its trajectory
A)both the velocity and the acceleration of the soccer ball are zero.
B)neither the ball's velocity nor its acceleration are zero.
C)the ball's acceleration is zero but its velocity is not zero.
D)the ball's acceleration points upward.
E)the ball's velocity points downward.
A)both the velocity and the acceleration of the soccer ball are zero.
B)neither the ball's velocity nor its acceleration are zero.
C)the ball's acceleration is zero but its velocity is not zero.
D)the ball's acceleration points upward.
E)the ball's velocity points downward.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
41
The components of vectors and are given as follows: = -9.2 = -4.5 = -6.1 = 4.3 The angle (less than 180°)between vectors and is closest to
A)77°.
B)103°.
C)10°.
D)170°.
E)84°.
A)77°.
B)103°.
C)10°.
D)170°.
E)84°.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
42
A vector has components Ax = 12.0 m and Ay = 5.00 m.
(a)What is the angle that vector makes with the +x-axis?
(b)What is the magnitude of vector ?
(a)What is the angle that vector makes with the +x-axis?
(b)What is the magnitude of vector ?

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
43
The x component of vector is 5.3 units, and its y component is -2.3 units. The angle that vector makes with the +x-axis is closest to
A)340°
B)160°
C)250°
D)110°
E)23°
A)340°
B)160°
C)250°
D)110°
E)23°

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
44
Two perpendicular vectors, and , are added together giving vector . If the magnitudes of both vectors and are doubled without changing their directions, the magnitude of vector will
A)increase by a factor of 8.
B)increase by a factor of 4.
C)increase by a factor of 2.
D)increase by a factor of .
E)not change.
A)increase by a factor of 8.
B)increase by a factor of 4.
C)increase by a factor of 2.
D)increase by a factor of .
E)not change.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
45
If vector has components Ax = -3.0 lb and Ay = -4.0 lb, and vector has components Bx = 3.0 lb and By = -8.0 lb, what is the magnitude of vector = - ?
A)13 lb
B)16 lb
C)140 lb
D)7.2 lb
A)13 lb
B)16 lb
C)140 lb
D)7.2 lb

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
46
When rolled down a mountainside at 7.0 m/s, the horizontal component of its velocity vector was 1.8 m/s. What was the angle of the mountain surface above the horizontal?
A)75°
B)57 °
C)33°
D)15°
A)75°
B)57 °
C)33°
D)15°

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
47
A displacement vector is 34.0 m in length and is directed 60.0° east of north. Selecting from the choices in the table below, what are the components of this vector?
A)choice 1
B)choice 2
C)choice 3
D)choice 4
E)choice 5
A)choice 1
B)choice 2
C)choice 3
D)choice 4
E)choice 5

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
48
The x and y components of a vector in a horizontal plane are 4.00 m and 3.00 m, respectively.
(a)What is the magnitude of this vector?
(b)What angle does this vector make with the positive +y-axis.
(a)What is the magnitude of this vector?
(b)What angle does this vector make with the positive +y-axis.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
49
A boy jumps with a velocity of magnitude 20.0 m/s at an angle of 25.0° above the horizontal. What is the horizontal component of the boy's velocity?
A)18.1 m/s
B)15.6 m/s
C)8.45 m/s
D)12.6 m/s
E)9.33 m/s
A)18.1 m/s
B)15.6 m/s
C)8.45 m/s
D)12.6 m/s
E)9.33 m/s

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
50
A car travels 20 km west and then 20 km south. What is the magnitude of its displacement vector?
A)0 km
B)20 km
C)28 km
D)40 km
A)0 km
B)20 km
C)28 km
D)40 km

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
51
Three ropes are tied in a knot as shown in the figure. One student pulls on rope A with 1.0 pound of force, and another student pulls on rope B with 7.0 pounds of force. How hard and in what direction must you pull on rope C to balance the first two pulls? Give the direction by specifying the angle (clockwise or counterclockwise)of the pull with the direction of rope A. 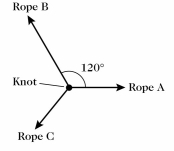


Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
52
When Jeff ran up a hill at 7.0 m/s, the horizontal component of his velocity vector was 5.1 m/s. What was the vertical component of Jeff's velocity?
A)4.8 m/s
B)4.3 m/s
C)3.8 m/s
D)3.4 m/s
A)4.8 m/s
B)4.3 m/s
C)3.8 m/s
D)3.4 m/s

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
53
You walk to the north, then turn 60° to your right and walk another How far are you from where you originally started?
A)68 m
B)39 m
C)75 m
D)35 m
A)68 m
B)39 m
C)75 m
D)35 m

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
54
A player throws a football 50.0 m at 61.0° north of west. What is the westward component of the displacement of the football?
A)64.7m
B)55.0 m
C)0.00 m
D)74.0 m
E)24.2 m
A)64.7m
B)55.0 m
C)0.00 m
D)74.0 m
E)24.2 m

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
55
Vector has magnitude 2 units and is directed to the north. Vector has magnitude and is directed to the south. Calculate the magnitude and direction of
A)7 units, north
B)7 units, south
C)3 units, north
D)3 units, south
A)7 units, north
B)7 units, south
C)3 units, north
D)3 units, south

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
56
You walk 53 m to the north, then you turn 60° to your right and walk another Determine the direction of your displacement vector. Express your answer as an angle relative to east.
A)63° N of E
B)50° N of E
C)57° N of E
D)69° N of E
A)63° N of E
B)50° N of E
C)57° N of E
D)69° N of E

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
57
A vector in the xy-plane has an x component of -7.50 units. What must be the y component of this vector so that its magnitude is 10.0 units. (Note: There are two possible answers.)

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
58
The x component of vector is 8.7 units, and its y component is -6.5 units. The magnitude of is closest to
A)9.9 units
B)7.9 units
C)8.9 units
D)11 units
E)12 units
A)9.9 units
B)7.9 units
C)8.9 units
D)11 units
E)12 units

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
59
The magnitude of is 5.5 m, and this vector lies in the second quadrant and makes an angle of 34 ° with the +y-axis. The components of are closest to:
A) = -3.1 m, = 4.6 m.
B) = 3.1 m, = -4.6 m.
C) = 4.6 m, = -3.1 m.
D) = -4.6 m, = 3.1 m.
E) = -4.6 m, = -3.1 m.
A) = -3.1 m, = 4.6 m.
B) = 3.1 m, = -4.6 m.
C) = 4.6 m, = -3.1 m.
D) = -4.6 m, = 3.1 m.
E) = -4.6 m, = -3.1 m.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
60
The components of vectors and are given as follows: Ax = 7.6 Bx = -5.1
Ay = -9.2 By = -6.8
What is the magnitude of the vector difference - ?
A)13
B)3.5
C)16
D)170
E)3.4
Ay = -9.2 By = -6.8
What is the magnitude of the vector difference - ?
A)13
B)3.5
C)16
D)170
E)3.4

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
61
Four vectors, , , , and , are shown in the figure. The sum of these four vectors is a vector having magnitude and direction 
A)4.0 cm, along +x-axis.
B)4.0 cm, along -x-axis.
C)4.0 cm, along +y-axis.
D)4.0 cm, along -y-axis.
E)4.0 cm, 45° above +x-axis.

A)4.0 cm, along +x-axis.
B)4.0 cm, along -x-axis.
C)4.0 cm, along +y-axis.
D)4.0 cm, along -y-axis.
E)4.0 cm, 45° above +x-axis.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
62
Two boys, Joe and Sam, who are searching for buried treasure start underneath the same tree. Joe walks 12 m east and then 12 m north, while Sam walks 15 m west and then 10 m south. Both boys then stop. Find the magnitude and direction of the vector from Sam to Joe. Express the direction of this vector by specifying the angle it makes with the west-to-east direction.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
63
Vector has a magnitude of 6.0 m and points 30° east of south. Vector has a magnitude of 4.0 m and points 30° west of north. The resultant vector + is given by
A)2.0 m at an angle of 30° north of west.
B)2.0 m at an angle of 30° east of south.
C)10.0 m at an angle of 60° north of west.
D)10.0 m at an angle of 60° east of south.
E)1.0 m at an angle of 60° north of west.
A)2.0 m at an angle of 30° north of west.
B)2.0 m at an angle of 30° east of south.
C)10.0 m at an angle of 60° north of west.
D)10.0 m at an angle of 60° east of south.
E)1.0 m at an angle of 60° north of west.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
64
The figure shows three vectors and their magnitudes and relative directions. The magnitude of the resultant of the three vectors is closest to 
A)19
B)16
C)13
D)10
E)7.0

A)19
B)16
C)13
D)10
E)7.0

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
65
Displacement vector is 5.5 cm long and points along the +x-axis. Displacement vector is 7.5 cm long and points at +30° to the -x-axis.
(a)Determine the x and y components of vector .
(b)Determine the x and y components of vector .
(c)Determine the x and y components of the resultant of these two vectors.
(d)Determine the magnitude and direction of the resultant of these two vectors.
(a)Determine the x and y components of vector .
(b)Determine the x and y components of vector .
(c)Determine the x and y components of the resultant of these two vectors.
(d)Determine the magnitude and direction of the resultant of these two vectors.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
66
Vector has a magnitude of 4.0 m and points 30° south of east. Vector has a magnitude of 2.0 m and points 30° north of west. The resultant vector + is given by
A)10.0 m at an angle 30° south of east.
B)10.0 m at an angle 60° east of south.
C)2.0 m at an angle 60° south of east.
D)2.0 m at an angle 30° south of east.
E)1.0 m at an angle 30° east of south.
A)10.0 m at an angle 30° south of east.
B)10.0 m at an angle 60° east of south.
C)2.0 m at an angle 60° south of east.
D)2.0 m at an angle 30° south of east.
E)1.0 m at an angle 30° east of south.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
67
Vector = 4.00 m points eastward and vector = 3.00 m points southward. The resultant vector + is given by
A)5.00 m at an angle of 36.9° south of east.
B)5.00 m at an angle of 53.1° south of east.
C)5.00 m at an angle of 71.6° south of east.
D)5.00 m at an angle of 18.4° south of east.
E)5.00 m at an angle of 26.6° south of east.
A)5.00 m at an angle of 36.9° south of east.
B)5.00 m at an angle of 53.1° south of east.
C)5.00 m at an angle of 71.6° south of east.
D)5.00 m at an angle of 18.4° south of east.
E)5.00 m at an angle of 26.6° south of east.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
68
Three forces, 1, 2, and 3, each of magnitude 70 N, all act on an object as shown in the figure. The magnitude of the resultant force acting on the object is 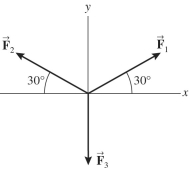
A)35 N.
B)70 N.
C)140 N.
D)210 N.
E)0 N.

A)35 N.
B)70 N.
C)140 N.
D)210 N.
E)0 N.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
69
Find the magnitude and direction of the resultant of the three force vectors, , , and , shown in the figure. These vectors have the following magnitudes: A = 5.0 lb, B = 7.9 lb, and C = 8.0 lb. Express the direction of the resultant by specifying the angle it makes with the +x-axis, with counterclockwise angles taken to be positive. 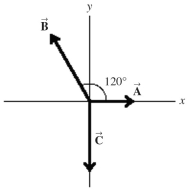


Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
70
Vector has a magnitude of 6.0 m and points 30° north of east. Vector has a magnitude of 4.0 m and points 30° east of north. The resultant vector + is given by
A)0.70 m at an angle of 42° north of east.
B)14 m at an angle of 42° north of east.
C)1.1 m at an angle of 42° north of east.
D)9.7 m at an angle of 42° north of east.
E)2.0 m at an angle of 42° north of east.
A)0.70 m at an angle of 42° north of east.
B)14 m at an angle of 42° north of east.
C)1.1 m at an angle of 42° north of east.
D)9.7 m at an angle of 42° north of east.
E)2.0 m at an angle of 42° north of east.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
71
Vector has a magnitude of 6.0 m and points 30° north of east. Vector has a magnitude of 4.0 m and points 30° west of south. The resultant vector + is given by
A)2.7 m at an angle of 8.3° south of east.
B)2.7 m at an angle of 8.3° east of south.
C)3.2 m at an angle of 8.3° east of south.
D)3.2 m at an angle of 8.3° south of east.
E)2.3 m at an angle of 8.3° south of east.
A)2.7 m at an angle of 8.3° south of east.
B)2.7 m at an angle of 8.3° east of south.
C)3.2 m at an angle of 8.3° east of south.
D)3.2 m at an angle of 8.3° south of east.
E)2.3 m at an angle of 8.3° south of east.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
72
An airplane undergoes the following displacements, all at the same altitude: First, it flies in a direction 30.0° east of north. Next, it flies due south. Finally, it flies 30.0° north of west. Use components to determine how far the airplane ends up from its starting point.
A)71.5 km
B)73.0 km
C)74.4 km
D)70.1 km
E)68.7 km
A)71.5 km
B)73.0 km
C)74.4 km
D)70.1 km
E)68.7 km

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
73
The figure shows two vectors and , along with their magnitudes and directions. The vector is given by = - . 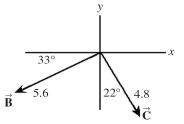 (a)What is the magnitude of vector ?
(a)What is the magnitude of vector ?
(b)What angle does vector make with the +x-axis?
 (a)What is the magnitude of vector ?
(a)What is the magnitude of vector ?(b)What angle does vector make with the +x-axis?

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
74
Three forces, 1, 2, and 3, all act on an object, as shown in the figure. The magnitudes of the forces are: F1 = 80.0 N, F2 = 60.0 N, and F3 = 40.0 N. The resultant force acting on the object is given by 
A)180 N at an angle of 60.0° with respect to +x-axis.
B)60.0 N at an angle of 90.0° with respect to +x-axis.
C)20.0 N at an angle of 34.3° with respect to +x-axis.
D)35.5 N at an angle of 34.3° with respect to +x-axis.
E)40.0 N at an angle of 60.0° with respect to +x-axis.

A)180 N at an angle of 60.0° with respect to +x-axis.
B)60.0 N at an angle of 90.0° with respect to +x-axis.
C)20.0 N at an angle of 34.3° with respect to +x-axis.
D)35.5 N at an angle of 34.3° with respect to +x-axis.
E)40.0 N at an angle of 60.0° with respect to +x-axis.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
75
Vector has a magnitude of 6.0 m and points 30° south of east. Vector has a magnitude of 4.0 m and points 30° west of south. The resultant vector + is given by
A)7.2 m at an angle of 64° south of east.
B)3.3 m at an angle of 64° south of east.
C)9.8 m at an angle of 26° south of east.
D)9.8 m at an angle of 64° south of east.
E)3.3 m at an angle of 26° south of east.
A)7.2 m at an angle of 64° south of east.
B)3.3 m at an angle of 64° south of east.
C)9.8 m at an angle of 26° south of east.
D)9.8 m at an angle of 64° south of east.
E)3.3 m at an angle of 26° south of east.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
76
Vector has a magnitude of 6.0 m and points 30° north of east. Vector has a magnitude of 4.0 m and points 30° west of north. The resultant vector + is given by
A)9.8 m at an angle of 64° east of north.
B)9.8 m at an angle of 26° north of east.
C)7.2 m at an angle of 26° east of north.
D)3.3 m at an angle of 26° north of east.
E)3.3 m at an angle of 64° east of north.
A)9.8 m at an angle of 64° east of north.
B)9.8 m at an angle of 26° north of east.
C)7.2 m at an angle of 26° east of north.
D)3.3 m at an angle of 26° north of east.
E)3.3 m at an angle of 64° east of north.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
77
Two forces are acting on an object as shown in the figure. Assume that all the quantities shown are accurate to three significant figures. 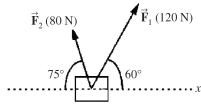 (a)What is the magnitude of the resultant force on the object?
(a)What is the magnitude of the resultant force on the object?
(b)What is the direction of the resultant force?
 (a)What is the magnitude of the resultant force on the object?
(a)What is the magnitude of the resultant force on the object?(b)What is the direction of the resultant force?

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
78
Vector has a magnitude of 8.0 m and points east, vector has a magnitude of 6.0 m and points north, and vector has a magnitude of 5.0 m and points west. The resultant vector + + is given by
A)2.0 m at an angle 63° north of east.
B)2.0 m at an angle 63° east of north.
C)6.7 m at an angle 63° east of north.
D)6.7 m at an angle 63° north of east.
E)3.8 m at an angle 67° north of east
A)2.0 m at an angle 63° north of east.
B)2.0 m at an angle 63° east of north.
C)6.7 m at an angle 63° east of north.
D)6.7 m at an angle 63° north of east.
E)3.8 m at an angle 67° north of east

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
79
Vector has a magnitude of 7.0 m and points 30° east of north. Vector has a magnitude of 5.0 m and points 30° west of south. The resultant vector + is given by
A)10.0 m at an angle 60° north of east.
B)10.0 m at an angle 30° east of north.
C)2.0 m at an angle 30° north of east.
D)2.0 m at an angle 60° north of east.
E)1.0 m at an angle 60° east of north
A)10.0 m at an angle 60° north of east.
B)10.0 m at an angle 30° east of north.
C)2.0 m at an angle 30° north of east.
D)2.0 m at an angle 60° north of east.
E)1.0 m at an angle 60° east of north

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck
80
Displacement vector is 75 cm long and points at 30° above the +x-axis. Displacement vector is 25 cm long and points along the -x-axis. Displacement vector is 40 cm long and points at 45° below the -x-axis.
(a)Determine the x and y components of vector .
(b)Determine the x and y components of vector .
(c)Determine the x and y components of vector .
(d)Determine the x and y components of the resultant of these three vectors.
(e)Determine the magnitude and direction of the resultant of these three vectors.
(a)Determine the x and y components of vector .
(b)Determine the x and y components of vector .
(c)Determine the x and y components of vector .
(d)Determine the x and y components of the resultant of these three vectors.
(e)Determine the magnitude and direction of the resultant of these three vectors.

Unlock Deck
Unlock for access to all 180 flashcards in this deck.
Unlock Deck
k this deck



