Deck 14: Optimization Models
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/114
Play
Full screen (f)
Deck 14: Optimization Models
1
If 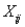 refers to the number of hours that employee
refers to the number of hours that employee 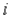 works in week
works in week 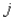 , then to indicate that the number of working hours of four employees in week 3 should not exceed 160 hours, we must have a constraint of the form:
, then to indicate that the number of working hours of four employees in week 3 should not exceed 160 hours, we must have a constraint of the form:
A)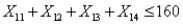
B)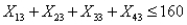

C)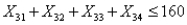
D)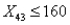
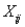 refers to the number of hours that employee
refers to the number of hours that employee 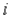 works in week
works in week 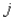 , then to indicate that the number of working hours of four employees in week 3 should not exceed 160 hours, we must have a constraint of the form:
, then to indicate that the number of working hours of four employees in week 3 should not exceed 160 hours, we must have a constraint of the form:A)
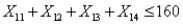
B)
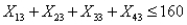

C)
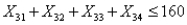
D)
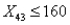
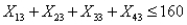

2
Many organizations must determine how to schedule employees to provide adequate service. If we assume that an organization faces the same situation each week, this is referred to as:
A) a static scheduling problem
B) a dynamic scheduling problem
C) a transportation scheduling problem
D) all of these choices
A) a static scheduling problem
B) a dynamic scheduling problem
C) a transportation scheduling problem
D) all of these choices
a static scheduling problem
3
When we solve a linear programming problem with Solver, we cannot guarantee that the solution obtained is an optimal solution.
False
4
Many of the most successful applications of optimization in the real world have been in the areas of scheduling, blending, logistics, and aggregate planning.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
5
What happens to the revenue when the optimal plan changes?

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
6
Integer programming (IP) models are optimization models in which all of the variables must be integers.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
7
The LP relaxation of an integer programming (IP) problem is the same model as the IP model except that some integer constraints are omitted.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
8
If Solver fails to find an optimal solution to an integer programming problem, we might be able to find a near optimal solution by increasing the Integer Optimality setting.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
9
Many organizations must determine how to schedule employees to provide adequate service. If we assume that an organization faces the same situation each week, this is referred to as:
A) a static scheduling problem
B) a dynamic scheduling problem
C) a transportation scheduling problem
D) all of these choices
A) a static scheduling problem
B) a dynamic scheduling problem
C) a transportation scheduling problem
D) all of these choices

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
10
If an LP problem is not correctly formulated, Solver will automatically indicate that it is infeasible when trying to solve it.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
11
The optimal solution to an LP problem was 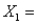 3.69 and
3.69 and 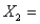 1.21. If
1.21. If 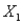 and
and 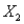 were restricted to be integers, then
were restricted to be integers, then 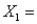 4 and
4 and 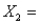 1 will be a feasible solution, but not necessarily an optimal solution to the IP problem.
1 will be a feasible solution, but not necessarily an optimal solution to the IP problem.
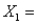 3.69 and
3.69 and 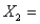 1.21. If
1.21. If 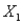 and
and 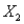 were restricted to be integers, then
were restricted to be integers, then 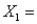 4 and
4 and 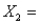 1 will be a feasible solution, but not necessarily an optimal solution to the IP problem.
1 will be a feasible solution, but not necessarily an optimal solution to the IP problem.
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
12
Transportation costs for a given route are nearly always linear and smooth, with the main cost differences occurring between routes.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
13
Rounding the solution of a linear programming problem to the nearest integer values provides a(n):
A) integer solution that is optimal
B) integer solution that may be neither feasible nor optimal
C) feasible solution that is not necessarily optimal
D) infeasible solution
A) integer solution that is optimal
B) integer solution that may be neither feasible nor optimal
C) feasible solution that is not necessarily optimal
D) infeasible solution

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
14
Workforce scheduling problems are often integer programming models, which means that they have:
A) an integer objective function
B) integer decision variables
C) integer constraints
D) all of these choices
A) an integer objective function
B) integer decision variables
C) integer constraints
D) all of these choices

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
15
Multiple optimal solutions are quite common in linear programming models.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
16
Solver may be unable to solve some integer programming problems, even when they have an optimal solution.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
17
Which of the following does not represent a broad class of applications of linear programming models?
A) blending models
B) financial portfolio models
C) logistics models
D) set covering models
E) forecasting models
A) blending models
B) financial portfolio models
C) logistics models
D) set covering models
E) forecasting models

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
18
A common characteristic of integer programming models is that they:
A) are easy to solve graphically
B) produce the same answer and standard linear programming models
C) often produce multiple optimal solutions
D) have all of these choices in common
A) are easy to solve graphically
B) produce the same answer and standard linear programming models
C) often produce multiple optimal solutions
D) have all of these choices in common

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
19
Which of these statements are true of multiple optimal solutions?
A) All solutions have the same values for the decision variables.
B) All solutions have the same value for the objective function.
C) All solutions have the same shadow prices.
D) All of these statements are true.
A) All solutions have the same values for the decision variables.
B) All solutions have the same value for the objective function.
C) All solutions have the same shadow prices.
D) All of these statements are true.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
20
Which of the following statements are false?
A) Solver does not offer a sensitivity report for models with integer constraints.
B) Solver's sensitivity report is not suited for questions about multiple input changes.
C) Solver's sensitivity report is used primarily for questions about one-at-a time changes to input.
D) None of these statements are false.
A) Solver does not offer a sensitivity report for models with integer constraints.
B) Solver's sensitivity report is not suited for questions about multiple input changes.
C) Solver's sensitivity report is used primarily for questions about one-at-a time changes to input.
D) None of these statements are false.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
21
To specify that 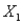 must be at most 75% of the blend of
must be at most 75% of the blend of 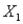 ,
, 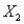 , and
, and 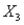 , we must have a constraint of the form:
, we must have a constraint of the form:
A)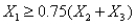
B)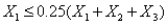
C)
D)
E)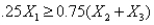
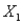 must be at most 75% of the blend of
must be at most 75% of the blend of 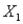 ,
, 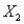 , and
, and 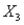 , we must have a constraint of the form:
, we must have a constraint of the form:A)
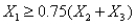
B)
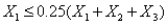
C)

D)

E)
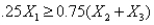

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
22
Suppose that later in the year, venison will be out of season, but the market will be able to obtain an additional 300 pounds of pork for the same costs. Develop a processing plan in that case. How does the solution change?

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
23
A post office requires different numbers of full-time employees on different days of the week. The number of full-time employees required each day is given in the table below. 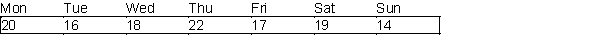 Union rules state that each full-time employee must work five consecutive days and then receive two days off. The post office wants to meet its daily requirements using only full-time employees. Its objective is to minimize the number of full-time employees that must be hired.
Union rules state that each full-time employee must work five consecutive days and then receive two days off. The post office wants to meet its daily requirements using only full-time employees. Its objective is to minimize the number of full-time employees that must be hired.
During each four-hour period, the police force in a small town in Ohio requires the following number of on-duty police officers: 8 from midnight to 4 A.M.; 7 from 4 A.M. to 8 A.M.; 6 from 8 A.M. to noon; 6 from noon to 4 P.M.; 5 from 4 P.M. to 8 P.M.; and 4 from 8 P.M. to midnight. Each police officer works two consecutive four-hour shifts. Determine how to minimize the number of police officers needed to meet the town's daily requirements.
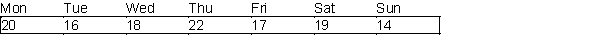 Union rules state that each full-time employee must work five consecutive days and then receive two days off. The post office wants to meet its daily requirements using only full-time employees. Its objective is to minimize the number of full-time employees that must be hired.
Union rules state that each full-time employee must work five consecutive days and then receive two days off. The post office wants to meet its daily requirements using only full-time employees. Its objective is to minimize the number of full-time employees that must be hired.During each four-hour period, the police force in a small town in Ohio requires the following number of on-duty police officers: 8 from midnight to 4 A.M.; 7 from 4 A.M. to 8 A.M.; 6 from 8 A.M. to noon; 6 from noon to 4 P.M.; 5 from 4 P.M. to 8 P.M.; and 4 from 8 P.M. to midnight. Each police officer works two consecutive four-hour shifts. Determine how to minimize the number of police officers needed to meet the town's daily requirements.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
24
In blending problems, if a quality constraint involves a quotient, then the problem will be nonlinear.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
25
A typical transportation problem requires which of the following sets of input numbers?
A) capacities, demands, and flows
B) capacities, demands, and unit shipping costs
C) supplies, demands, and flows
D) supplies, demands, and arcs
A) capacities, demands, and flows
B) capacities, demands, and unit shipping costs
C) supplies, demands, and flows
D) supplies, demands, and arcs

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
26
A construction company is preparing for a nine-month project, and will need to develop a staffing plan. The company can assign up to 30 of its own full-time employees to the project, and will hire short-term contract employees to make up any shortage in meeting the personnel requirements. Company employees earn $6,000 per month, while short-term contract employees make $8,600/month. Contract employees can be assigned to the project beginning in any month, and their contract period is two months. The number of workers required for the project by month is shown below:
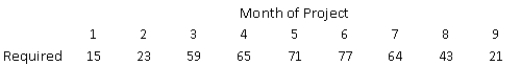
Determine the optimal staffing plan for this project.
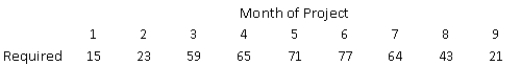
Determine the optimal staffing plan for this project.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
27
The constraints in a blending problem can be specified in a valid way and still lead to which of the following problems?
A) unboundedness
B) insensitivity
C) nonlinearity
D) none of these choices
A) unboundedness
B) insensitivity
C) nonlinearity
D) none of these choices

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
28
Which of the following is a type of constraint often required in blending problems?
A) integer constraint
B) binary constraint
C) quality constraint
D) none of these choices
A) integer constraint
B) binary constraint
C) quality constraint
D) none of these choices

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
29
The project manager is evaluating options to complete the project early so that the company can earn a bonus. He has determined that the project schedule can be compressed into a six-month schedule, with the same total number of worker-months. In that case, the staffing requirements are as shown below. 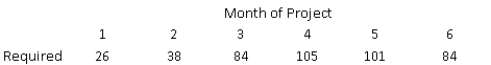 Develop an optimal staffing plan for the project under the accelerated schedule.
Develop an optimal staffing plan for the project under the accelerated schedule.
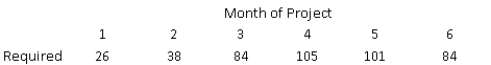 Develop an optimal staffing plan for the project under the accelerated schedule.
Develop an optimal staffing plan for the project under the accelerated schedule.
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
30
A problem that deals with the direct distribution of products from supply locations to demand locations is called a(n):
A) transportation problem
B) assignment problem
C) network problem
D) transshipment problem
A) transportation problem
B) assignment problem
C) network problem
D) transshipment problem

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
31
The production manager believes the cost of the contract employees, who are currently in high demand, could be somewhat higher - perhaps as high as $10,000 per month. Perform a sensitivity analysis to determine the effect on the number of full-time employees that will be needed for the project.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
32
A company has daily staffing requirements for two types of jobs, cleaning and customer service persons. The minimum numbers of workers required each day for each type of job are shown in the table below. To meet these requirements, the company can employ three types of workers: those who clean only, those who can perform customer service only, and those who are able to do both. In each of these three categories, the company wants to meet its daily requirements using only full-time workers. A full-time worker must work five consecutive days with two days off. Workers who are able to perform only one type of work (cleaning or customer service) earn $50 per day. Those who are able to perform both types of work earn $60 per day. As a matter of policy, the company wants to ensure that at least 20% of its total hours are staffed by "swing workers"; those who can do both types of jobs. The company wants to find a staffing policy that covers the daily worker requirements at minimum total costs per week. Use solver to formulate and solve the company's problem. 


Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
33
A Michigan company consists of three subsidiaries. Each has the respective average payroll, unemployment reserve fund, and estimated payroll shown in the table below (all figures are in millions of dollars). Any employer in the state of Michigan whose reserve to average payroll ratio is less than 1 must pay 25% of its estimated payroll in unemployment insurance premiums. Otherwise, if the ratio is at least one, the employer pays 13%. The company can aggregate its subsidiaries and label them as separate employers. For example, if subsidiaries 1 and 2 are aggregated, they must pay 25% of their combined payroll in unemployment insurance premiums. Determine which subsidiaries should be aggregated. 


Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
34
The objective in transportation problems is typically to:
A) maximize profits
B) maximize revenue
C) minimize costs
D) maximize feasibility
A) maximize profits
B) maximize revenue
C) minimize costs
D) maximize feasibility

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
35
A post office requires different numbers of full-time employees on different days of the week. The number of full-time employees required each day is given in the table below. 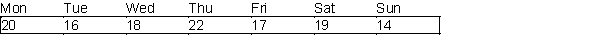 Union rules state that each full-time employee must work five consecutive days and then receive two days off. The post office wants to meet its daily requirements using only full-time employees. Its objective is to minimize the number of full-time employees that must be hired.
Union rules state that each full-time employee must work five consecutive days and then receive two days off. The post office wants to meet its daily requirements using only full-time employees. Its objective is to minimize the number of full-time employees that must be hired.
(A) Use Solver to formulate and solve the post office's problem.
(B) Suppose the post office has 30 full-time employees and is not allowed to hire or fire any employees. Determine a schedule that maximizes the number of weekend days off received by the employees.
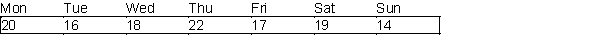 Union rules state that each full-time employee must work five consecutive days and then receive two days off. The post office wants to meet its daily requirements using only full-time employees. Its objective is to minimize the number of full-time employees that must be hired.
Union rules state that each full-time employee must work five consecutive days and then receive two days off. The post office wants to meet its daily requirements using only full-time employees. Its objective is to minimize the number of full-time employees that must be hired.(A) Use Solver to formulate and solve the post office's problem.
(B) Suppose the post office has 30 full-time employees and is not allowed to hire or fire any employees. Determine a schedule that maximizes the number of weekend days off received by the employees.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
36
A company blends silicon and nitrogen to produce two types of fertilizers. Fertilizer 1 must be at least 40% nitrogen and sells for $75 per pound. Fertilizer 2 must be at least 70% silicon and sells for $45 per pound. The company can purchase up to 9000 pounds of nitrogen at $16 per pound and up to 12,000 pounds of silicon at $12 per pound. Assuming that all fertilizer produced can be sold, determine how the company can maximize its profit.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
37
Determine the optimal processing plan for the meat market.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
38
You have decided to enter the candy business. You are considering producing two types of candies: A and B, both of which consist solely of sugar, nuts, and chocolate. At present you have in stock 12,000 ounces of sugar, 3000 ounces of nuts, and 3000 ounces of chocolate. The mixture used to make candy A must contain at least 10% nuts and 10% chocolate. The mixture used to make candy B must contain at least 20% nuts. Each ounce of candy A can be sold for $0.40 and each ounce of candy for $0.50. Determine how you can maximize your revenues from candy sales.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
39
The market manager is concerned about variability in the fat content of beef, noting that it actually can be as high as 20% and as low as 5%. Perform a sensitivity analysis to determine the effect, first on the amount of beef used, and then on the revenue. What do the results indicate? Should the manager be concerned?

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
40
Suppose the bonus for completing the project three months early is $250,000. What would be the net bonus to the company, after adjusting for any difference in personnel costs under the accelerated schedule?

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
41
The decision variables in transportation problems are:
A) profits
B) costs
C) flows
D) capacities
A) profits
B) costs
C) flows
D) capacities

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
42
If all the supplies and demands for a transportation model are integers, then the optimal Solver solution may or may not have integer-valued shipments.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
43
Transportation and transshipment problems are both considered special cases of a class of linear programming problems called:
A) minimum cost problems
B) minimum cost network flow problems
C) supply locations network problems
D) demand locations network problems
A) minimum cost problems
B) minimum cost network flow problems
C) supply locations network problems
D) demand locations network problems

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
44
The flow balance constraint for each transshipment node, in a minimum cost network flow model, takes which form?
A) Net Outflow = Capacity
B) Net Outflow < Capacity
C) Net Inflow=0 (equivalent to Net Outflow=0)
D) Net Inflow ≥ Demand
E) Net Inflow = Demand
A) Net Outflow = Capacity
B) Net Outflow < Capacity
C) Net Inflow=0 (equivalent to Net Outflow=0)
D) Net Inflow ≥ Demand
E) Net Inflow = Demand

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
45
In transportation problem, shipping costs are often nonlinear due to quantity discounts.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
46
In transportation problems, the three sets of input numbers that are required are capacities, demands, and flows.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
47
Which of the following is not a required input for a typical transportation problem?
A) capacities (or supplies)
B) demands
C) unit shipping (and possibly production) costs
D) distance from origins to destinations
A) capacities (or supplies)
B) demands
C) unit shipping (and possibly production) costs
D) distance from origins to destinations

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
48
The transportation model is a special case of the minimum cost network flow model (MCNFM).

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
49
In network models of transportation problems, arcs represent the routes for getting a product from one node to another.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
50
Logistics problems are problems of finding the least expensive way to transport products from their origin to their destination.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
51
In a network representation of a transportation problem, the nodes generally represent:
A) warehouses
B) geographic locations
C) flows
D) capacities
A) warehouses
B) geographic locations
C) flows
D) capacities

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
52
In a transshipment problem, shipments:
A) can occur between any two nodes (suppliers, demanders, and transshipment locations)
B) cannot occur between two supply locations
C) cannot occur between two demand locations
D) cannot occur between a transshipment location and a demand location
E) cannot occur between a supply location and a demand location
A) can occur between any two nodes (suppliers, demanders, and transshipment locations)
B) cannot occur between two supply locations
C) cannot occur between two demand locations
D) cannot occur between a transshipment location and a demand location
E) cannot occur between a supply location and a demand location

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
53
In a network representation of a transportation problem, the arcs generally represent:
A) warehouses
B) geographic locations
C) flows
D) capacities
A) warehouses
B) geographic locations
C) flows
D) capacities

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
54
In a minimum cost network flow model, the flow balance constraint for each supply node takes which form?
A) Net Inflow = Demand
B) Net Inflow ≥ Demand
C) Net Inflow=0 (equivalent to Net Outflow=0)
D) Net Outflow ≤ Capacity
E) Net Outflow > Capacity
A) Net Inflow = Demand
B) Net Inflow ≥ Demand
C) Net Inflow=0 (equivalent to Net Outflow=0)
D) Net Outflow ≤ Capacity
E) Net Outflow > Capacity

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
55
Transshipment points are locations where goods neither originate nor end up, but goods are allowed to enter such points to be shipped out to their eventual destinations.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
56
In a typical minimum cost network flow model, the nodes indicate:
A) roads
B) rail lines
C) geographic locations
D) rivers
A) roads
B) rail lines
C) geographic locations
D) rivers

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
57
In a minimum cost network flow model, the flow balance constraint for each demand node takes which form?
A) Net Outflow > Capacity
B) Net Inflow ≥ Demand
C) Net Inflow=0 (equivalent to Net Outflow=0)
D) Net Outflow ≤ Capacity
A) Net Outflow > Capacity
B) Net Inflow ≥ Demand
C) Net Inflow=0 (equivalent to Net Outflow=0)
D) Net Outflow ≤ Capacity

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
58
In transportation problems, shipments between supply points or between demand points are possible.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
59
In a transportation problem, if it costs $4 per item to ship up to 200 items between cities, and $2 per item for each additional item, the proportionality assumption of LP is satisfied.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
60
In formulating a transportation problem as linear programming model, which of the following statements are correct?
A) There is one constraint for each supply location.
B) There is one constraint for each demand location.
C) The sum of decision variables out of a supply location is constrained by the supply at that location.
D) The sum of decision variables out of all supply locations to a specific demand location is constrained by the demand at that location.
E) All of these statements are correct
A) There is one constraint for each supply location.
B) There is one constraint for each demand location.
C) The sum of decision variables out of a supply location is constrained by the supply at that location.
D) The sum of decision variables out of all supply locations to a specific demand location is constrained by the demand at that location.
E) All of these statements are correct

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
61
In an optimized network flow model (MCNFM), all the available capacity will be used.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
62
During the next four quarters, an automobile company must meet (on time) the following demands for cars: 4000 in quarter 1; 2000 in quarter 2; 5000 in quarter 3; 1000 in quarter 4. At the beginning of quarter 1, there are 300 autos in stock. The company has the capacity to produce at most 3000 cars per quarter. At the beginning of each quarter, the company can change production capacity. It costs $100 to increase quarterly production capacity by 1 unit. For example, it would cost $20,000 to increase capacity from 3000 to 3200. It also costs $60 per quarter to maintain each unit of production capacity (even if it is unused during the current quarter). The variable cost of producing a car is $2200. A holding cost of $160 per car is assessed against each quarter's ending inventory. It is required that at the end of quarter 4, plant capacity must be at least 4000 cars. Determine how to minimize the total cost incurred during the next 4 quarters.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
63
An oil delivery truck contains five compartments, holding up to 2800, 2900, 1200, 1800, and 3200 gallons of fuel, respectively. The company must deliver three types of fuel (super, regular, and unleaded) to a customer. The demands, penalty per gallon short, and the maximum allowed shortage are shown in the table below. Each compartment of the truck can carry only one type of gasoline. Determine how to load the truck in a way that minimizes shortage costs. 


Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
64
An auto company must meet (on time) the following demands for cars: 5000 in quarter 1; 3000 in quarter 2; 6000 in quarter 3; 2000 in quarter 4. At the beginning of quarter 1, there are 500 autos in stock. The company has the capacity to produce at most 3600 cars per quarter. At the beginning of each quarter, the company can change production capacity. It costs $125 to increase quarterly production capacity by one unit. It also costs $60 per quarter to maintain each unit of production capacity (even if it is unused during the current quarter). The variable cost of producing a car is $2400. A holding cost of $200 per car is assessed against each quarter's ending inventory. It is required that at the end of quarter 4, plant capacity must be at least 5000 cars. Determine how to minimize the total cost incurred during the next four quarters.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
65
A company manufactures two products. If it charges price 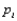 for product I, it can sell
for product I, it can sell 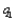 units of product I, where
units of product I, where 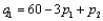 and
and 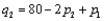 . It costs $25 to produce a unit of product 1 and $72 to produce a unit of product 2. How many units of each product should the company produce, and what prices should it charge, to maximize its profit?
. It costs $25 to produce a unit of product 1 and $72 to produce a unit of product 2. How many units of each product should the company produce, and what prices should it charge, to maximize its profit?
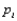 for product I, it can sell
for product I, it can sell 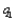 units of product I, where
units of product I, where 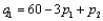 and
and 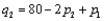 . It costs $25 to produce a unit of product 1 and $72 to produce a unit of product 2. How many units of each product should the company produce, and what prices should it charge, to maximize its profit?
. It costs $25 to produce a unit of product 1 and $72 to produce a unit of product 2. How many units of each product should the company produce, and what prices should it charge, to maximize its profit?
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
66
The cost per day running a hotel is 200,000 + 0.002 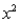 dollars, where x is the number of customers served per day. What number of customers served per day minimizes the cost per customer of running the hotel?
dollars, where x is the number of customers served per day. What number of customers served per day minimizes the cost per customer of running the hotel?
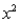 dollars, where x is the number of customers served per day. What number of customers served per day minimizes the cost per customer of running the hotel?
dollars, where x is the number of customers served per day. What number of customers served per day minimizes the cost per customer of running the hotel?
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
67
A company supplies goods to three customers, each of whom requires 50 units. The company has two warehouses. In Warehouse 1, 75 units are available, and in Warehouse 2, 55 units are available. The costs of shipping one unit from each warehouse to each customer are shown in the table below.  There is a penalty for each unsatisfied customer unit of demand - with customer 1, a penalty cost of $100 is incurred; with customer 2, $90; and with customer 3, $115.
There is a penalty for each unsatisfied customer unit of demand - with customer 1, a penalty cost of $100 is incurred; with customer 2, $90; and with customer 3, $115.
Suppose that the company can purchase and ship extra units to either warehouse for a total cost of $125 per unit and that all customer demand must be met. Determine how to minimize the sum of purchasing and shipping costs.
 There is a penalty for each unsatisfied customer unit of demand - with customer 1, a penalty cost of $100 is incurred; with customer 2, $90; and with customer 3, $115.
There is a penalty for each unsatisfied customer unit of demand - with customer 1, a penalty cost of $100 is incurred; with customer 2, $90; and with customer 3, $115.Suppose that the company can purchase and ship extra units to either warehouse for a total cost of $125 per unit and that all customer demand must be met. Determine how to minimize the sum of purchasing and shipping costs.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
68
A large accounting firm has three auditors. Each can work up to 180 hours during the next month, during which time three projects must be completed. Project 1 takes 140 hours, Project 2 takes 150 hours, and Project 3 takes 170 hours. The amount per hour that can be billed for assigning each auditor to each project is given in the table below: 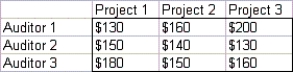 Determine how to maximize total billings during the next month by formulating the company's problem as a transportation model.
Determine how to maximize total billings during the next month by formulating the company's problem as a transportation model.
 Determine how to maximize total billings during the next month by formulating the company's problem as a transportation model.
Determine how to maximize total billings during the next month by formulating the company's problem as a transportation model.
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
69
Aggregate planning models are usually implemented through a rolling planning horizon.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
70
In aggregate planning models, we can model backlogging of demand by allowing a month's inventory to be negative.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
71
In aggregate planning models, which of the following statements are correct?
A) The number of workers available influences the possible production levels.
B) We allow the workforce level to be modified each month through the hiring and firing of workers.
C) We eventually allow demand to be backlogged; that is, demand need not be met on time.
D) All of these choices are correct.
A) The number of workers available influences the possible production levels.
B) We allow the workforce level to be modified each month through the hiring and firing of workers.
C) We eventually allow demand to be backlogged; that is, demand need not be met on time.
D) All of these choices are correct.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
72
An oil company controls two oil fields. Field 1 can produce up to 45 million barrels of oil per day, and Field 2 can produce up to 55 million barrels of oil per day. At Field 1, it costs $3 to extract and refine a barrel of oil; at Field 2, the cost is $2. The company sells oil to two countries: France and Japan. The shipping costs per barrel are shown below.  Each day, France is willing to buy up to 45 million barrels (at $6 per barrel), and Japan is willing to buy up to 35 million barrels (at $6.50 per barrel). Determine how to maximize the company's profit.
Each day, France is willing to buy up to 45 million barrels (at $6 per barrel), and Japan is willing to buy up to 35 million barrels (at $6.50 per barrel). Determine how to maximize the company's profit.
 Each day, France is willing to buy up to 45 million barrels (at $6 per barrel), and Japan is willing to buy up to 35 million barrels (at $6.50 per barrel). Determine how to maximize the company's profit.
Each day, France is willing to buy up to 45 million barrels (at $6 per barrel), and Japan is willing to buy up to 35 million barrels (at $6.50 per barrel). Determine how to maximize the company's profit.
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
73
An oil company produces oil at two wells. Well 1 can produce up to 150,000 barrels per day, and Well 2 can produce up to 200,000 barrels per day. It is possible to ship oil directly from the wells to customers in Los Angeles and New York. Alternatively, the company could transport oil to the ports of Mobile and Galveston and then ship it by tanker to New York or Los Angeles. Los Angeles requires 160,000 barrels per day, and New York requires 140,000 barrels per day. The costs (in dollars) of shipping 1000 barrels between various locations are shown below: 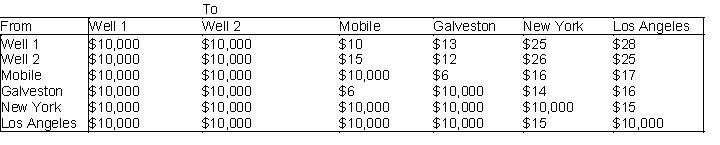
(A) Assume that before being shipped to Los Angeles or New York, all oil produced at the wells must be refined at either Mobile or Galveston. To refine 10000 barrels of oil costs $12 at Mobile and $10 at Galveston. Assuming that both Mobile and Galveston have infinite refinery capacity, determine how to minimize the daily cost of transporting and refining the oil requirements of Los Angeles and New York.
(B) Rework (A) under the assumption that Galveston has a refinery capacity of 150,000 barrels per day, and Mobile has a refinery capacity of 180,000 barrels per day.

(A) Assume that before being shipped to Los Angeles or New York, all oil produced at the wells must be refined at either Mobile or Galveston. To refine 10000 barrels of oil costs $12 at Mobile and $10 at Galveston. Assuming that both Mobile and Galveston have infinite refinery capacity, determine how to minimize the daily cost of transporting and refining the oil requirements of Los Angeles and New York.
(B) Rework (A) under the assumption that Galveston has a refinery capacity of 150,000 barrels per day, and Mobile has a refinery capacity of 180,000 barrels per day.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
74
The cost per day of running a hospital is 250,000 + 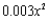 dollars, where x is the number of patients served per day. What number of patients served per day minimizes the cost per patient of running the hospital?
dollars, where x is the number of patients served per day. What number of patients served per day minimizes the cost per patient of running the hospital?
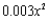 dollars, where x is the number of patients served per day. What number of patients served per day minimizes the cost per patient of running the hospital?
dollars, where x is the number of patients served per day. What number of patients served per day minimizes the cost per patient of running the hospital?
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
75
An auto company produces cars at Los Angeles and Detroit, and has a warehouse in Atlanta. The company supplies cars to dealers in Dallas and Orlando. The costs of shipping a car between various points are shown in the table below, where "NA" means that a shipment is not allowed. Los Angeles can produce up to 1400 cars, and Detroit can produce up to 3200 cars. Dallas must receive 2800 cars, and Orlando must receive 1800 cars. 
(A) Determine how to minimize the cost of meeting demands at Dallas and Orlando.
(B) Modify the answer to (A) if shipments between Los Angeles and Detroit are not allowed.

(A) Determine how to minimize the cost of meeting demands at Dallas and Orlando.
(B) Modify the answer to (A) if shipments between Los Angeles and Detroit are not allowed.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
76
A company supplies goods to three customers, each of whom requires 50 units. The company has two warehouses. In Warehouse 1, 75 units are available, and in Warehouse 2, 55 units are available. The costs of shipping one unit from each warehouse to each customer are shown in the table below.  There is a penalty for each unsatisfied customer unit of demand - with customer 1, a penalty cost of $100 is incurred; with customer 2, $90; and with customer 3, $115.
There is a penalty for each unsatisfied customer unit of demand - with customer 1, a penalty cost of $100 is incurred; with customer 2, $90; and with customer 3, $115.
Determine how to minimize the sum of shortage and shipping costs.
 There is a penalty for each unsatisfied customer unit of demand - with customer 1, a penalty cost of $100 is incurred; with customer 2, $90; and with customer 3, $115.
There is a penalty for each unsatisfied customer unit of demand - with customer 1, a penalty cost of $100 is incurred; with customer 2, $90; and with customer 3, $115.Determine how to minimize the sum of shortage and shipping costs.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
77
In aggregate planning models, the number of workers available influences the possible production levels.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
78
An oil company has oil fields in San Diego and Los Angeles. The San Diego field can produce up to 500,000 barrels per day, and the Los Angeles field can produce up to 400,000 barrels per day. Oil is sent from the fields to a refinery, either in Dallas or in Houston. Assume that each refinery has unlimited capacity. To refine 100,000 barrels costs $725 at Dallas and $950 at Houston. Refined oil is shipped to customers in Chicago and New York. Chicago customers require 400,000 barrels per day, and New York customers require 300,000 barrels per day. The costs of shipping 100,000 barrels of oil (refined or unrefined) between cities are shown in the table below: 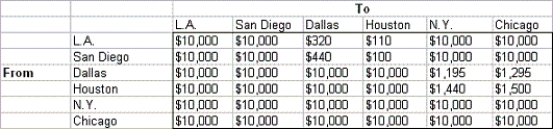
(A) Determine how to minimize the total cost of meeting all demands.
(B) If each refinery had a capacity of 380,000 barrels per day, how would you modify the model in (A)?

(A) Determine how to minimize the total cost of meeting all demands.
(B) If each refinery had a capacity of 380,000 barrels per day, how would you modify the model in (A)?

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
79
Each year, a computer company produces up to 600 computers in New York and up to 500 computers in Memphis. Los Angeles customers must receive 600 computers, and 500 computers must be supplies to Oklahoma City customers. Producing a computer costs $850 in New York and $950 in Memphis. Computers are transported by plane and can be sent through Chicago. The costs of shipping a computer between cities are shown below. 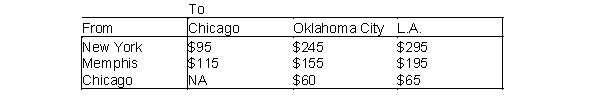
(A) Determine how to minimize the total (production plus distribution) costs of meeting the company's annual demand.
(B) How would you modify the model in (A) if at most 300 units can be shipped through Chicago?
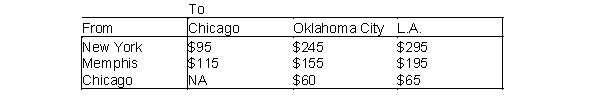
(A) Determine how to minimize the total (production plus distribution) costs of meeting the company's annual demand.
(B) How would you modify the model in (A) if at most 300 units can be shipped through Chicago?

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
80
The flows in a general minimum cost network flow model (MCNFM) all have to be from "left to right"; that is, from supply points to demand points.

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck



