Deck 3: The Time Value of Money Private
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/42
Play
Full screen (f)
Deck 3: The Time Value of Money Private
1
The present value of an annuity due exceeds thepresent value of an ordinary annuity.
True
2
The concept of the time value of money is a meansto bring together the present and the future.
True
3
Compounding refers to the earning of interest on interest earned previously.
True
4
Discounting
A) expresses the present in the future
B) brings the future back to the present
C) is synonymous with compounding
D) depends on the rate of interest
A) expresses the present in the future
B) brings the future back to the present
C) is synonymous with compounding
D) depends on the rate of interest

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
5
The present value of an annuity increases as thenumber of years increases.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
6
The present value of a dollar1. increases as the interest rate increases2. decreases as the interest rate increases3. increases as the time period increases4. decreases as the time period increases
A) 1 and 3
B) 1 and 4
C) 2 and 3
D) 2 and 4
A) 1 and 3
B) 1 and 4
C) 2 and 3
D) 2 and 4

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
7
The future value of an annuity is1. larger the higher the rate of interest2. smaller the higher the rate of interest3. larger the greater the number of years4. smaller the greater the number of years
A) 1 and 3
B) 1 and 4
C) 2 and 3
D) 2 and 4
A) 1 and 3
B) 1 and 4
C) 2 and 3
D) 2 and 4

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
8
The future value of a dollar1. increases with higher interest rates2. decreases with higher interest rates3. increases as the time period increases4. decreases as the time period increases
A) 1 and 3
B) 1 and 4
C) 2 and 3
D) 2 and 4
A) 1 and 3
B) 1 and 4
C) 2 and 3
D) 2 and 4

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
9
If interest rates are 0 percent, an annuity of $100for ten years is the same as $1,000 today.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
10
The present value of a dollar increases as thenumber of years increases.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
11
Which is the largest if the interest rate is7 percent
A) $100 compounded for three years
B) the future value of a $100 annuity for three years
C) the present value of $100 after three years
D) the present value of a $100 annuity
A) $100 compounded for three years
B) the future value of a $100 annuity for three years
C) the present value of $100 after three years
D) the present value of a $100 annuity

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
12
An annuity is a series of
A) rising annual payments
B) random payments
C) equal payments
D) unequal payments
A) rising annual payments
B) random payments
C) equal payments
D) unequal payments

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
13
The future value of an annuity of $100 at 3 percentfor ten years exceeds $1,000.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
14
A series of equal payments is called an annuity.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
15
If the first payment made by an annuity is today, that is an "ordinary annuity" and not an "annuity due."

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
16
The future value of an ordinary annuity will exceedthe future value of an annuity due.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
17
The present value of an annuity due is not affected by the frequency of compounding.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
18
The larger the rate of interest, the smaller is thefuture value of a dollar.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
19
An increase in the rate of interest from 4 percent to 5 percent increases the present value of an annuity.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
20
If a bank pays 2 percent compounded daily, the truerate of interest is greater than 2 percent.

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
21
Worker A annually invests $1,000 in an IRA for nine years (ages 27 through 35) and never makes another contribution. Worker B annually invests $1,000 in an IRA for thirty years (ages 36 through 65). Which worker will have more in his or her account when he or she retires if they both earn 8 percent on their investments

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
22
The present value of an annuity is1. larger the greater the rate of interest2. smaller the greater the rate of interest3. larger as the number of years increases4. smaller as the number of years increases
A) 1 and 3
B) 1 and 4
C) 2 and 3
D) 2 and 4
A) 1 and 3
B) 1 and 4
C) 2 and 3
D) 2 and 4

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
23
AIR National's capacity is 120 passengers per flight. It currently carries 74 passengers per flight. Growth in passengers is expected to be 6 percent annually. New plans will have to be ordered when the company is carrying 90 percent of capacity. How long will it be before the firm must order new planes

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
24
Time value concepts may be used to determine1. the annual growth rate in dividends2. the amount in an IRA account after ten years3. the tax owed on a capital gain
A) 1 and 2
B) 1 and 3
C) 2 and 3
D) only 2
A) 1 and 2
B) 1 and 3
C) 2 and 3
D) only 2

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
25
The future value of an annuity will be larger if1. the annuity is an ordinary annuity2. the annuity is an annuity due3. the payments are made at the beginning of the year4. the payments are made at the end of the year
A) $10,000 + ... + $10,000 = $10,000(7.722) (1 + .05) (1 + .05)10
X = $77,220
(N = 10; I = 5; PMT = 10000; FV = 0; PV = ? = -77217.)
A) 1 and 3
B) $10,000(12.578) = $125,780 (PV = 0; N = 10; I = 5; PMT = -10000; FV = ? = 125779.)
8) Planes will have to be ordered when the firm is carrying 108 passengers (120 x .9). This is a future value problem:
74(1 + .06)n = 108
Interest factor = 108/74 = 1.459
Using the interest table for the future value of $1, the answer is between 6 and 7 years. (PV = -74; I = 6; PMT = 0; FV = 90; N = ? = 6.49.)
9) 1(1 + .1)5(1 + .05)5 = $2.055
(PV = -1; N = 5; I = 10; PMT = 0; FV = ? = 1.61.)
(PV = -1.61; N = 5; I = 5; PMT = 0; FV = ? = 2.05.)
10) Worker A: $1,000(12.488)(10,063) = $125,660
(PV = 0; N = 9; I = 8; PMT = -1000; FV = ? = 12488.)
(PV = -12488; N = 30; I = 8; PMT = 0;
FV = ? = 125662.)
Worker B: $1,000(113.283) = $113,283
(PV = 0; N = 30; I = 8; PMT = -1000; FV = ? = 113283.)
(I don't know a better means to illustrate the importance of early contributions to a retirement account than this type of problem. Worker A only contributed $9,000 while Worker B put in $30,000, but Worker A ends with the larger terminal value.)
11) Maximum price:
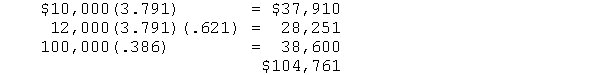 (Since the cash inflows vary, this problem requires using a calculator that accepts annual unequal payments.)
(Since the cash inflows vary, this problem requires using a calculator that accepts annual unequal payments.)
12) Present value of the payments
 (The $100,000 settlement does not look so attractive when expressed in terms of present value.)
(The $100,000 settlement does not look so attractive when expressed in terms of present value.)
13) This problem may be solved as a future value or a present value of a dollar since the present and future amounts are known, but the rate is the unknown. As a future value problem, the answer is
$10,000(1 + r)15 = $100,000
FVIF = $100,000/$10,000 = 10
Using the future value table, the return is about 16 percent
As a present value problem, the answer is
PVIF = $10,000/$100,000 = 0.1
Using the present value table, the return is about 16 percent.
The use of a financial calculator is the same whether the problem is viewed as a present value of future value perspective.
(PV = -10000; I = ?; N = 15; PMT = 0, and FV = 100,000
I = 16.59.)
14) This is another simple problem that asks for the annual payment to accumulate a specified sum. However, the payments start after five years have passed, so the number of years is 10 and not 15.
PMT(IFFVA at 8% for 10 years) = $1,000,000
PMT(14.487) = $1,000,000
PMT = 69,027
(PV = 0; I = 8; N = 10; FV = 1000000, and PMT = ?
PMT = 69029.)
15) Sinking funds are covered in Chapter 13 on bonds. To meet this requirement, the fund must annually invest $62,746.
PMT(IFFVA at 10% for 10 years) = $1,000,000
X(15.937) = $1,000,000
X = $1,000,000/15.937 = $62,747
15)937 is the interest factor for the future value of $1 at 10% for 10 years.
(PV = 0; N = 10; I = 10; PMT = ?, and FV = 1000000.
PMT = -62745.39.)
16) This problem illustrates that when time value of money is considered, states distribute a small proportion of the funds they receive through the sale of lotto tickets.
As stated, the problem is an example of the present value of an annuity due. The present value of the promised payments is
$560,000(9.818)(1.08) = $5,937,930.
9)818 is the interest factor for the present value of the ordinary annuity at 8% for 20 years, and the 1.08 converts the interest factor into the interest factor for an annuity due.
The state will distribute 27.1 percent of the ticket sales:
$5,937,930/$21,900,000 = 27.1%.
Since most lotto winners take the lump sum instead of the annual payments, the problem could be reworded as follows. You have the choice to take an immediate lump sum payment of $5,800,000 or receive $560,000 a year for twenty years. If you can earn 8 percent on invested funds, which alternative is better? Since the present value of the payments is $5,937,930, that alternative is to be preferred. (It is doubtful that lottery winners make that calculation!)
17) In order to earn 10 percent annually, the sale price must be $3,984,900.
(PV = 10000000; N = 4; I = 10; PMT = 2000000;
FV = ? = 3,894000.)
The answer is $2,673,880 if the rent payments are made at the beginning of the year (i.e., the problem is treated as an illustration of an annuity due).
B) 1 and 4
C) 2 and 3
A) $10,000 + ... + $10,000 = $10,000(7.722) (1 + .05) (1 + .05)10
X = $77,220
(N = 10; I = 5; PMT = 10000; FV = 0; PV = ? = -77217.)
A) 1 and 3
B) $10,000(12.578) = $125,780 (PV = 0; N = 10; I = 5; PMT = -10000; FV = ? = 125779.)
8) Planes will have to be ordered when the firm is carrying 108 passengers (120 x .9). This is a future value problem:
74(1 + .06)n = 108
Interest factor = 108/74 = 1.459
Using the interest table for the future value of $1, the answer is between 6 and 7 years. (PV = -74; I = 6; PMT = 0; FV = 90; N = ? = 6.49.)
9) 1(1 + .1)5(1 + .05)5 = $2.055
(PV = -1; N = 5; I = 10; PMT = 0; FV = ? = 1.61.)
(PV = -1.61; N = 5; I = 5; PMT = 0; FV = ? = 2.05.)
10) Worker A: $1,000(12.488)(10,063) = $125,660
(PV = 0; N = 9; I = 8; PMT = -1000; FV = ? = 12488.)
(PV = -12488; N = 30; I = 8; PMT = 0;
FV = ? = 125662.)
Worker B: $1,000(113.283) = $113,283
(PV = 0; N = 30; I = 8; PMT = -1000; FV = ? = 113283.)
(I don't know a better means to illustrate the importance of early contributions to a retirement account than this type of problem. Worker A only contributed $9,000 while Worker B put in $30,000, but Worker A ends with the larger terminal value.)
11) Maximum price:
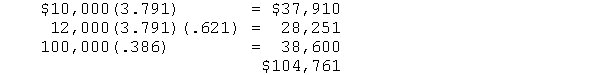 (Since the cash inflows vary, this problem requires using a calculator that accepts annual unequal payments.)
(Since the cash inflows vary, this problem requires using a calculator that accepts annual unequal payments.)12) Present value of the payments
 (The $100,000 settlement does not look so attractive when expressed in terms of present value.)
(The $100,000 settlement does not look so attractive when expressed in terms of present value.)13) This problem may be solved as a future value or a present value of a dollar since the present and future amounts are known, but the rate is the unknown. As a future value problem, the answer is
$10,000(1 + r)15 = $100,000
FVIF = $100,000/$10,000 = 10
Using the future value table, the return is about 16 percent
As a present value problem, the answer is
PVIF = $10,000/$100,000 = 0.1
Using the present value table, the return is about 16 percent.
The use of a financial calculator is the same whether the problem is viewed as a present value of future value perspective.
(PV = -10000; I = ?; N = 15; PMT = 0, and FV = 100,000
I = 16.59.)
14) This is another simple problem that asks for the annual payment to accumulate a specified sum. However, the payments start after five years have passed, so the number of years is 10 and not 15.
PMT(IFFVA at 8% for 10 years) = $1,000,000
PMT(14.487) = $1,000,000
PMT = 69,027
(PV = 0; I = 8; N = 10; FV = 1000000, and PMT = ?
PMT = 69029.)
15) Sinking funds are covered in Chapter 13 on bonds. To meet this requirement, the fund must annually invest $62,746.
PMT(IFFVA at 10% for 10 years) = $1,000,000
X(15.937) = $1,000,000
X = $1,000,000/15.937 = $62,747
15)937 is the interest factor for the future value of $1 at 10% for 10 years.
(PV = 0; N = 10; I = 10; PMT = ?, and FV = 1000000.
PMT = -62745.39.)
16) This problem illustrates that when time value of money is considered, states distribute a small proportion of the funds they receive through the sale of lotto tickets.
As stated, the problem is an example of the present value of an annuity due. The present value of the promised payments is
$560,000(9.818)(1.08) = $5,937,930.
9)818 is the interest factor for the present value of the ordinary annuity at 8% for 20 years, and the 1.08 converts the interest factor into the interest factor for an annuity due.
The state will distribute 27.1 percent of the ticket sales:
$5,937,930/$21,900,000 = 27.1%.
Since most lotto winners take the lump sum instead of the annual payments, the problem could be reworded as follows. You have the choice to take an immediate lump sum payment of $5,800,000 or receive $560,000 a year for twenty years. If you can earn 8 percent on invested funds, which alternative is better? Since the present value of the payments is $5,937,930, that alternative is to be preferred. (It is doubtful that lottery winners make that calculation!)
17) In order to earn 10 percent annually, the sale price must be $3,984,900.
(PV = 10000000; N = 4; I = 10; PMT = 2000000;
FV = ? = 3,894000.)
The answer is $2,673,880 if the rent payments are made at the beginning of the year (i.e., the problem is treated as an illustration of an annuity due).
B) 1 and 4
C) 2 and 3

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
26
You wish to have $100,000 after ten years for a major purchase such as a boat. How much must you invest at the end of each year if you earn 8 percent annually on your funds

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
27
A state's lottery winner is promised $200,000 a year for twenty years (starting at the end of the first year). How much must the state invest now to guarantee the prize if the state can earn annually 7 percent on its funds How much must the state invest if the annual payments are to be made at the beginning of the year

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
28
Time value concepts may not be used to determine
A) the present value of an annuity
B) the margin required on a stock purchase
C) the future value of $100 deposited in a bank
D) the present value of a lump sum
A) the present value of an annuity
B) the margin required on a stock purchase
C) the future value of $100 deposited in a bank
D) the present value of a lump sum

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
29
You are hurt in a car accident and your lawyer wins a $100,000 settlement to be distributed as follows:$20,000 immediate payment$5,000 a year for ten years$30,000 after ten years.If the lawyer's fee is $10,000, what is the value of this settlement if the interest rate is 6 percent

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
30
Which is the smallest if the interest rate is8 percent
A) $100 to be received after five years
B) the present value of an annuity of $100 for five years
C) $100 received in the present
D) $100 received for two years
A) $100 to be received after five years
B) the present value of an annuity of $100 for five years
C) $100 received in the present
D) $100 received for two years

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
31
Your brother, who is prone to bearing substantial risk, suggests that you buy a security for $10,000 that promises to pay you $100,000 at the end of 15 years. What is the implied annual return or yield on this investment

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
32
An investor expects the price of a stock to double after eight years. What is the expected annual rate of growth

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
33
If you open an IRA and invest $3,000 a year (at the end of the year), how much will be in the account after twenty five years if the funds earn 5 percent annually How much would be in the account if payments were made at the beginning of the year

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
34
A homeowner has a ten year home-improvement loan for $36,875. What are the annual payments required by the loan if the annual rate of interest is 4 percent

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
35
EEM, INC has a $1,000,000 debt outstanding that is due after 15 years. The contract required that after five years, the firm must set aside annually an amount so the debt is retired in full at maturity. If EEM can earn 8 percent on invested funds, how much must the company set aside each year

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
36
A firm currently earns $1.00 per share. A financial analyst believes that earnings will grow annually at the rate of 10 percent for five years and then decline to 5 percent. What are the expected earnings after ten years

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
37
Your uncle plans to leave you an inheritance of $200,000. If his life expectancy is twenty years, what is your inheritance currently worth if the anticipated return on investments is 9 percent

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
38
A firm has a $1,000,000 debt (e.g., a bond) outstanding that matures after 10 years. The sinking fund requires the firm to set aside annually an amount so the debt may be retired at maturity. If the firm can earn 10% annually on these funds, how much must it invest annually to meet the sinking fund

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
39
An investment offers $10,000 at the end of each year for ten years. (a) If you can earn 5 percent annually, what is this investment worth today (b) If you do not spend the annual payment but invest it at 5 percent, how much will you have after the ten years have lapsed

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
40
A piece of rental property will generate $10,000 a year for five years, $12,000 for the next five years, and then be sold at the end of the tenth year for $100,000. If you can earn 10 percent on your funds, what is the maximum you should pay for the property

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
41
You purchase a building for $10,000,000 and lease it for $2,000,000 a year for four years (i.e., collect annual rent payments). At the end of the four years, you plan to sell the building. If you want to earn 10 percent on your investment, how much must you receive from the sale SOLUTIONS TO PROBLEMS

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck
42
A state lotto awarded a prize of $560,000 a year for the next 20 years starting today. If the state sold $21,900,000 in lotto tickets, what proportion of the sales will the state distribute if it earns 8% annually on invested funds

Unlock Deck
Unlock for access to all 42 flashcards in this deck.
Unlock Deck
k this deck



