Deck 5: Summarizing Bivariate Data
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/37
Play
Full screen (f)
Deck 5: Summarizing Bivariate Data
1
One of the properties of Pearson's r is: "The value of r does not depend on the unit of measurement for either variable." In your own words, what does this mean?
If there is a correlation between two quantities, the value for r will be the same as regardless of the units of measure. For example, if there is a correlation between height and weight of Elementary School students when they are measured in inches and pound, the correlation coefficient will be exactly the same if they are measured in centimeters and kilograms.
2
The slopes of the least squares lines for predicting y from x, and the least squares line for predicting x from y, are equal.
False
3
Pearson's correlation coefficient, r, does not depend on the units of measurement of the two variables.
True
4
If on average y increases as x increases, the correlation coefficient is positive.

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
5
The breeding success of birds that nest on the ground can be affected by the depth of winter snow in high altitudes. The plot below relates the percentage of White-tailed Ptarmigan hens hatching at least one egg, to the amount of snowfall in the Sierra Nevadas that winter. 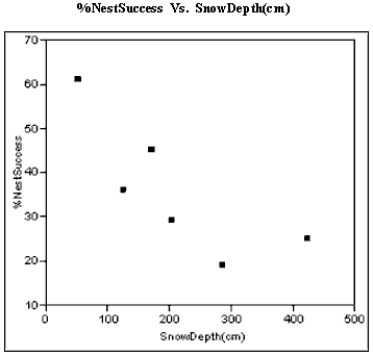 a) The least squares best fit line is %NestSuccess = 55.1816 − 0.092(SnowDepth). Graph this line using the axes above. Show any calculations in the space below. b) The least squares line is the line that minimizes the sum of the squared residuals. On the graph above pick 2 points and sketch the residuals associated with those points.
a) The least squares best fit line is %NestSuccess = 55.1816 − 0.092(SnowDepth). Graph this line using the axes above. Show any calculations in the space below. b) The least squares line is the line that minimizes the sum of the squared residuals. On the graph above pick 2 points and sketch the residuals associated with those points.
 a) The least squares best fit line is %NestSuccess = 55.1816 − 0.092(SnowDepth). Graph this line using the axes above. Show any calculations in the space below. b) The least squares line is the line that minimizes the sum of the squared residuals. On the graph above pick 2 points and sketch the residuals associated with those points.
a) The least squares best fit line is %NestSuccess = 55.1816 − 0.092(SnowDepth). Graph this line using the axes above. Show any calculations in the space below. b) The least squares line is the line that minimizes the sum of the squared residuals. On the graph above pick 2 points and sketch the residuals associated with those points.
Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
6
The least squares line passes through the point 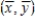 .
.
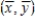 .
.
Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
7
The value of the residual plus  is equal to yi.
is equal to yi.
 is equal to yi.
is equal to yi.
Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
8
The data below were gathered on a random sample of 5 basking sharks, swimming through the water and filter-feeding, i.e. passively letting the water bring food into their mouths. 
a) What is the value of the correlation coefficient for these data?
b) What is the equation of the least squares line describing the relationship between x = body length and y = mean speed.
c) If these sharks are representative of the population of basking sharks, what would you predict is the mean speed for a filter-feeding basking shark that is 5.0 meters in length? Show any calculations below.
d) The largest basking shark in the sample is measured as 6.5 meters long. Theory predicts a maximum length of about 12.26 meters. Would it be reasonable to use the equation from part (b) above to predict the mean filter-feeding speed for a 12 meter long basking shark? Why or why not?

a) What is the value of the correlation coefficient for these data?
b) What is the equation of the least squares line describing the relationship between x = body length and y = mean speed.
c) If these sharks are representative of the population of basking sharks, what would you predict is the mean speed for a filter-feeding basking shark that is 5.0 meters in length? Show any calculations below.
d) The largest basking shark in the sample is measured as 6.5 meters long. Theory predicts a maximum length of about 12.26 meters. Would it be reasonable to use the equation from part (b) above to predict the mean filter-feeding speed for a 12 meter long basking shark? Why or why not?

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
9
If a scatter plot exhibits a strong negative relationship, what can be said about the value of the quantity,  ?
?
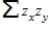 ?
?
Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
10
The coefficient of determination is equal to the positive square root of Pearson's r.

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
11
What is it that the Pearson correlation coefficient quantifies?

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
12
The standard deviation about the least squares line is roughly the typical amount by which an observation deviates from the least squares line.

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
13
A transformation, or reexpression, of a variable is accomplished by substituting a function of the variable in place of the variable for further analysis.

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
14
If |r| = 1, the standard deviation of y is equal to the standard deviation of the residuals.

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
15
If r is close to 1, then the points lie close to a straight line with a positive slope.

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
16
One of the properties of Pearson's r is: "The value of r does not depend on which of the two variables is labeled as x." In your own words, what does this mean?

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
17
The higher the value of the coefficient of determination, the greater the evidence for a causal relationship between x and y.

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
18
If a scatter plot exhibits a strong positive relationship, what can be said about the value of the quantity, 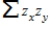 ?
?
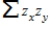 ?
?
Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
19
The value of Pearson's r is always between 0 and 1.

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
20
The slope of the least squares line is the average amount by which y increases as x increases by one unit.

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
21
If a correlation coefficient r is close to 0, there is no relationship between two variables.

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
22
Polar bear cubs are born in the winter in dens, and they must live off the fat stores of the mother even after leaving the den for sea ice, since the availability of their prey is unpredictable. Therefore, maternal weight is an important factor in successful reproduction of polar bears. In a recent spring, 261 adult females with 492 cubs were captured as they left their dens, and the mothers' weight and ages were determined by "counting annuli in the cementum of an extracted vestigial premolar tooth." (We are NOT making this up!) A quadratic fit of the maternal weight in kilograms to age in years resulted in the regression analysis below. 
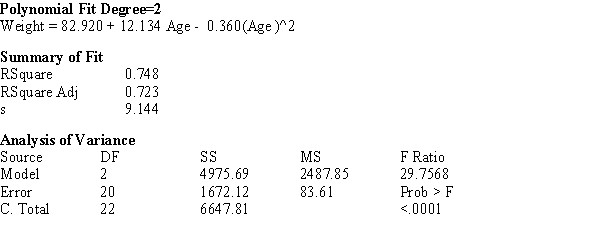
a) On average, about how far off are the weights of the maternal bears? That is, what is a typical difference between the actual weights and the weights predicted by the quadratic model?
b) If the maternal weight is an important factor as discussed above, what age of the female would seem to be the best for reproduction success? In a few sentences, justify your answer by appealing to the information provided above.


a) On average, about how far off are the weights of the maternal bears? That is, what is a typical difference between the actual weights and the weights predicted by the quadratic model?
b) If the maternal weight is an important factor as discussed above, what age of the female would seem to be the best for reproduction success? In a few sentences, justify your answer by appealing to the information provided above.

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
23
The Des Moines Register recently reported the ratings of high school sportsmanship as compiled by the Iowa High School Athletic Association. For each school the spectators and participants were rated by referees, where 1 = superior, and 5 = unsatisfactory. A regression analysis of the average scores given to wrestling spectators and wrestlers is shown below. 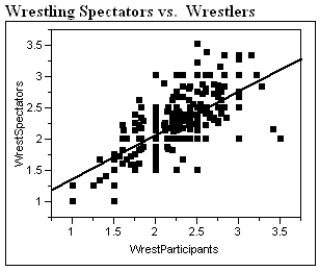

a) Interpret the correlation between the ratings of spectators and wrestlers.
b) Interpret the coefficient of determination.
c) Interpret the value of the standard deviation about the least squares line.


a) Interpret the correlation between the ratings of spectators and wrestlers.
b) Interpret the coefficient of determination.
c) Interpret the value of the standard deviation about the least squares line.

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
24
A cause-and-effect relationship between two variables is not the only reason of strong correlation.

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
25
A common statistical method for estimating a population size assumes each member of the population has an equal probability of being captured. To assess this assumption for crocodile populations, investigators repeatedly sampled sections of rivers in Australia. Crocodile lengths were measured in size classes. Crocs 0.0 - 0.3 meters in length are in size class 1, 0.3 - 0.6 meters in length are size class 2, etc. The normal maximum adult length is in a class size of 9 or 10. The investigators fit a quadratic function relating the probability of capture and the size class of captured crocodiles. The output from their analysis is shown below. 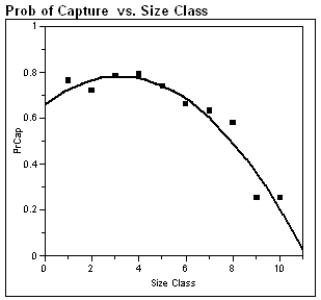

(a) What proportion of the variability in probability of capture is explained by the crocodile's size class?
(b) Some biologists speculate that as crocodiles grow they become more wary of humans, and are more difficult to detect in the wild. Support or refute this belief by appealing to the analysis above.


(a) What proportion of the variability in probability of capture is explained by the crocodile's size class?
(b) Some biologists speculate that as crocodiles grow they become more wary of humans, and are more difficult to detect in the wild. Support or refute this belief by appealing to the analysis above.

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
26
An ice cream seller wants to predict y = the number of ice creams sold when temperature (x) is 25 °C. Determine the types of variables.
A) y is a response variable, x is an explanatory variable
B) y is an explanatory variable, x is a response variable
C) y is an independent variable, x is an explanatory variable
D) y is an independent variable, x is a dependent variable
E) y is a response variable, x is a dependent variable
A) y is a response variable, x is an explanatory variable
B) y is an explanatory variable, x is a response variable
C) y is an independent variable, x is an explanatory variable
D) y is an independent variable, x is a dependent variable
E) y is a response variable, x is a dependent variable

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
27
The data below were gathered on a random sample of 7 male black-footed albatrosses of known age. In an effort to monitor diseases of these animals, biologists would like to be able to estimate the age of animals that have died by flattening their gonads and measuring the resulting area. 
a) What is the value of the correlation coefficient for these data?
b) What is the equation of the least squares line describing the relationship between x = Gonad Size and y = Age.
c) If these albatrosses are representative of the population, what would you predict to be the age of a male albatross with a gonad size of 50 sq. mm? Show any calculations below.
d) The largest albatross gonad size in the sample was 96 sq. mm, with an age of 23.64 years. These animals are thought to live for up to 40 years. Would it be reasonable to use the equation from part (b) above to predict the age for a gonad size of 150 sq. mm? Why or why not?

a) What is the value of the correlation coefficient for these data?
b) What is the equation of the least squares line describing the relationship between x = Gonad Size and y = Age.
c) If these albatrosses are representative of the population, what would you predict to be the age of a male albatross with a gonad size of 50 sq. mm? Show any calculations below.
d) The largest albatross gonad size in the sample was 96 sq. mm, with an age of 23.64 years. These animals are thought to live for up to 40 years. Would it be reasonable to use the equation from part (b) above to predict the age for a gonad size of 150 sq. mm? Why or why not?

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
28
One of the problems when estimating the size of animal populations from aerial surveys is that animals may bunch together, making it difficult to distinguish and count them accurately. For example, a horse standing alone is easy to spot; if seven horses huddled close together some may be missed, resulting in an undercount. The relative frequency of undercounts is typically reported as a percent. For example, if there are 10 horses in a group, a person in the plane may typically count fewer than 10 horses 20% of the time. In a recent study, the percent of sightings that resulted in an undercount was related to the size of the "group" of horses and donkeys; the following data were gathered:  After fitting a straight line model,
After fitting a straight line model, 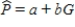 , significant curvature was detected in the residual plot, and two nonlinear models were chosen for further analysis, the exponential and the power models. The computer output for these models is given below, and the residual plots follow.
, significant curvature was detected in the residual plot, and two nonlinear models were chosen for further analysis, the exponential and the power models. The computer output for these models is given below, and the residual plots follow. 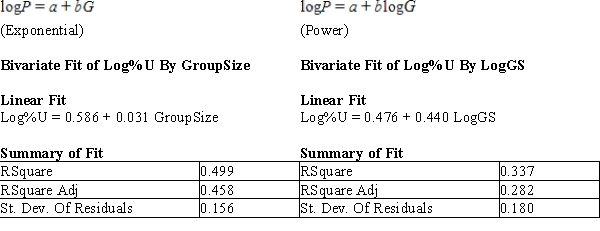 Residual Plots
Residual Plots 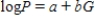
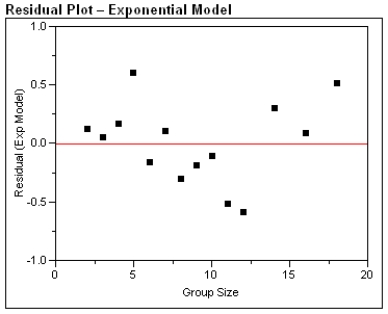
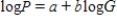
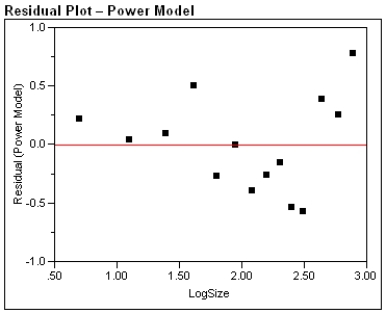
a) For the exponential model, calculate the predicted log (%undercount) for a group size = 10.
b) Use your calculations from part (a) to predict the %undercount for a group size = 10.
c) Generally speaking, which of the two models, power or exponential, is better at predicting the log (Percent Undercount)? Provide statistical justification for your choice.
 After fitting a straight line model,
After fitting a straight line model, 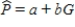 , significant curvature was detected in the residual plot, and two nonlinear models were chosen for further analysis, the exponential and the power models. The computer output for these models is given below, and the residual plots follow.
, significant curvature was detected in the residual plot, and two nonlinear models were chosen for further analysis, the exponential and the power models. The computer output for these models is given below, and the residual plots follow.  Residual Plots
Residual Plots 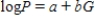

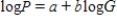

a) For the exponential model, calculate the predicted log (%undercount) for a group size = 10.
b) Use your calculations from part (a) to predict the %undercount for a group size = 10.
c) Generally speaking, which of the two models, power or exponential, is better at predicting the log (Percent Undercount)? Provide statistical justification for your choice.

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
29
The correlation coefficient between the consumption of ice cream and sales of bottled water is r = 0.76. This implies that a significant amount of consumed ice cream causes an increased demand for water.

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
30
Assessing the goodness of fit of a regression line involves considering different information, and no single characteristic of data is sufficient for a good assessment. Consider the characteristics below. How does each contribute to an assessment of fit? That is, for each piece of information, what about it would indicate a "good" best-fit line?
a) The shape of the scatter plot
b) The correlation coefficient
c) The standard deviation of the residuals
d) The coefficient of determination
a) The shape of the scatter plot
b) The correlation coefficient
c) The standard deviation of the residuals
d) The coefficient of determination

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
31
Exhibit 5-5
During the first 3 centuries AD, the Roman Empire produced coins in the Eastern provinces. Some historians argue that not all these coins were produced in local mints, and further that the mint of Rome struck some of them. Because the "style" of coins is difficult to analyze, the historians would like to use metallurgical analysis as one tool to identify the source mints of these coins. Investigators studied 11 coins known to have been produced by local mints in an attempt to identify a trace element profile for these coins, and have identified gold and lead as possible factors in identifying other coins as having been locally minted. The gold and lead content, measured as a % of weight of each coin, is given in the table, and a scatter plot of these data is presented below.
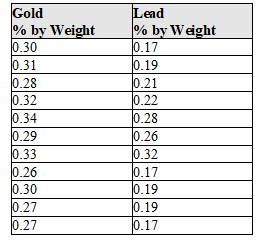
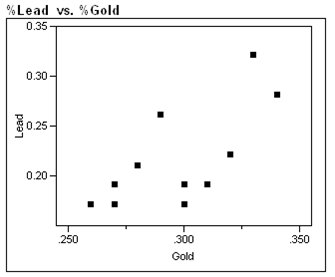
Suppose that the locally minted coins analyzed in Exhibit 5-5 are representative of the metallurgical content of mints in the Eastern provinces of the Roman Empire during the first 300 years AD.
a) If a locally minted coin is selected at random, and it's gold content is 0.30% by weight, calculate the predicted lead content. Be sure to use correct notation and units.
b) One of the coins used to calculate the regression equations has a gold content of 0.300%. Calculate the residual for this coin. Be sure to use correct notation and units.
c) The investigators would like to use the regression equation to help assess whether a coin is locally minted or minted in Rome. In a few sentences, describe how the regression equation could be used for this purpose. (Hint: In order to use the equation for this purpose, how would coins minted in Rome have to differ from locally minted coins?)
During the first 3 centuries AD, the Roman Empire produced coins in the Eastern provinces. Some historians argue that not all these coins were produced in local mints, and further that the mint of Rome struck some of them. Because the "style" of coins is difficult to analyze, the historians would like to use metallurgical analysis as one tool to identify the source mints of these coins. Investigators studied 11 coins known to have been produced by local mints in an attempt to identify a trace element profile for these coins, and have identified gold and lead as possible factors in identifying other coins as having been locally minted. The gold and lead content, measured as a % of weight of each coin, is given in the table, and a scatter plot of these data is presented below.


Suppose that the locally minted coins analyzed in Exhibit 5-5 are representative of the metallurgical content of mints in the Eastern provinces of the Roman Empire during the first 300 years AD.
a) If a locally minted coin is selected at random, and it's gold content is 0.30% by weight, calculate the predicted lead content. Be sure to use correct notation and units.
b) One of the coins used to calculate the regression equations has a gold content of 0.300%. Calculate the residual for this coin. Be sure to use correct notation and units.
c) The investigators would like to use the regression equation to help assess whether a coin is locally minted or minted in Rome. In a few sentences, describe how the regression equation could be used for this purpose. (Hint: In order to use the equation for this purpose, how would coins minted in Rome have to differ from locally minted coins?)

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
32
The use of small aircraft with human observers is common in wildlife studies where the goal is to estimate the abundance of different species. Recently there has been interest in using unmanned aerial vehicles (UAV). The UAV, something about the size of a model airplane, would fly over the area of interest and take pictures to be analyzed by computers with imagery software when the UAV returns. The plot below is from a test run of the UAV over 10 areas in South Central Florida, using bird decoys to test the reliability of the process. 
(a) The least squares best fit line is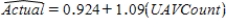 . Plot this line on the graph above. Show any calculations in the space below.
. Plot this line on the graph above. Show any calculations in the space below.
(b) The least squares line is the line that minimizes the sum of the squared residuals. On the graph above pick 2 points and sketch the residuals associated with those points.

(a) The least squares best fit line is
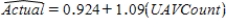 . Plot this line on the graph above. Show any calculations in the space below.
. Plot this line on the graph above. Show any calculations in the space below. (b) The least squares line is the line that minimizes the sum of the squared residuals. On the graph above pick 2 points and sketch the residuals associated with those points.

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
33
An independent, or explanatory, variable is the variable whose value should be predicted. A dependent, or response, variable is used to make a prediction of the independent variable

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
34
The Des Moines Register recently reported the ratings of high school sportsmanship as compiled by the Iowa High School Athletic Association. For each school the participants and coaches were rated by referees, where 1 = superior, and 5 = unsatisfactory. A regression analysis of the average scores given to football players and coaches is shown below. 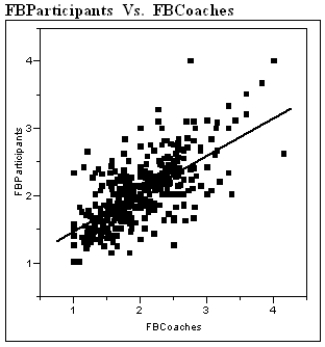 Linear Fit FBParticipants = 0.902 + 0.568 FBCoaches
Linear Fit FBParticipants = 0.902 + 0.568 FBCoaches 

a) Interpret the value of the correlation between the ratings of coaches and participants.
b) Interpret the value of the coefficient of determination.
c) Interpret the value of the standard deviation about the least squares line.
 Linear Fit FBParticipants = 0.902 + 0.568 FBCoaches
Linear Fit FBParticipants = 0.902 + 0.568 FBCoaches 

a) Interpret the value of the correlation between the ratings of coaches and participants.
b) Interpret the value of the coefficient of determination.
c) Interpret the value of the standard deviation about the least squares line.

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
35
When children and adolescents are discharged from the hospital the parents may still provide substantial care, such as the insertion of a feeding tube through the nose and down the esophagus into the stomach. It is difficult for parents to know how far to insert the tube, especially with rapidly growing infants. It may be possible for parents to measure their child's height and from that calculate the appropriate insertion length using a regression equation. At a major children's hospital, children and adolescents' heights and esophageal lengths were measured and a regression analysis performed. The data from this analysis is summarized below:  r = 0.995,
r = 0.995,  = 11.476 + 0.181H a) For a child with a height one standard deviation above the mean, what would be the predicted esophageal length? b) What proportion of the variability in esophageal length is accounted for by the height of the children and adolescents? c) From the information presented above, does it appear that the esophagus length can be accurately predicted from the height of young patients? Provide statistical evidence for your response.
= 11.476 + 0.181H a) For a child with a height one standard deviation above the mean, what would be the predicted esophageal length? b) What proportion of the variability in esophageal length is accounted for by the height of the children and adolescents? c) From the information presented above, does it appear that the esophagus length can be accurately predicted from the height of young patients? Provide statistical evidence for your response.
 r = 0.995,
r = 0.995,  = 11.476 + 0.181H a) For a child with a height one standard deviation above the mean, what would be the predicted esophageal length? b) What proportion of the variability in esophageal length is accounted for by the height of the children and adolescents? c) From the information presented above, does it appear that the esophagus length can be accurately predicted from the height of young patients? Provide statistical evidence for your response.
= 11.476 + 0.181H a) For a child with a height one standard deviation above the mean, what would be the predicted esophageal length? b) What proportion of the variability in esophageal length is accounted for by the height of the children and adolescents? c) From the information presented above, does it appear that the esophagus length can be accurately predicted from the height of young patients? Provide statistical evidence for your response.
Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
36
As early as 3 years of age, children begin to show preferences for playing with members of their own sex, and report having more same-sex than opposite-sex friends. In a study of 3rd and 4th graders' views on 48 personality traits, children were asked to rate on a "5-point" scale: 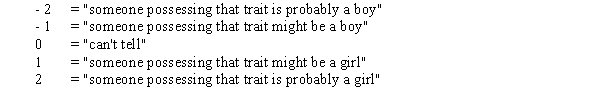 A plot of the data is presented below. A single point represents the (average girls' rating, average boys' rating) for a given trait.
A plot of the data is presented below. A single point represents the (average girls' rating, average boys' rating) for a given trait. 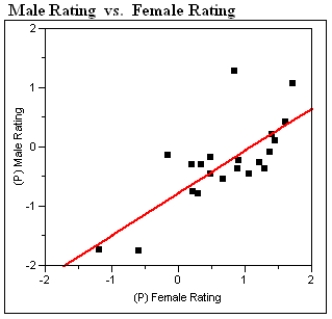
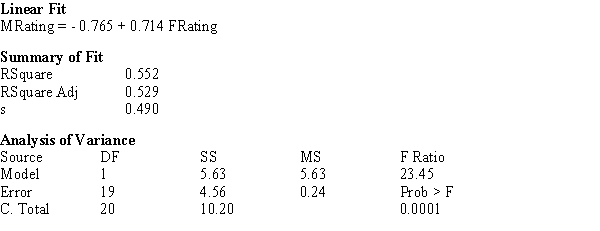
a) Circle the single point which represents the most influential observation. What aspect of this point makes it the most influential?
b) Suppose a personality trait similar to those used in the survey were given a 0.0 rating ("can't tell") by the girls. The predicted boys' average rating would be closest to which of the 5 categories described above?
c) The traits plotted above are those the researchers believe are "positive" traits, such as "mature," "honest," and "polite." The researchers thought that girls would rate these positive traits as characteristic of girls to a greater extent than boys would. What aspects of the plot and/or regression analysis presented above are consistent with this thinking?
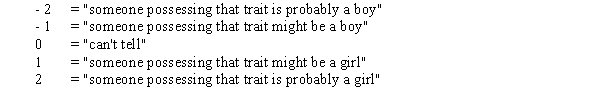 A plot of the data is presented below. A single point represents the (average girls' rating, average boys' rating) for a given trait.
A plot of the data is presented below. A single point represents the (average girls' rating, average boys' rating) for a given trait. 

a) Circle the single point which represents the most influential observation. What aspect of this point makes it the most influential?
b) Suppose a personality trait similar to those used in the survey were given a 0.0 rating ("can't tell") by the girls. The predicted boys' average rating would be closest to which of the 5 categories described above?
c) The traits plotted above are those the researchers believe are "positive" traits, such as "mature," "honest," and "polite." The researchers thought that girls would rate these positive traits as characteristic of girls to a greater extent than boys would. What aspects of the plot and/or regression analysis presented above are consistent with this thinking?

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
37
Exhibit 5-4
Biological theory suggests that the relationship between the weight of these animals and their wing length is exponential, i.e. W = α(10)βL, or W = α(e)βL where W is the wing weight and L is the wing length.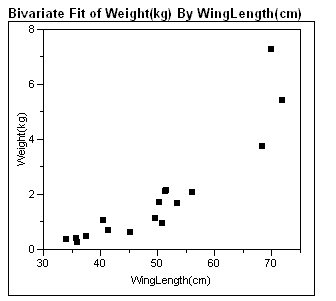
The model W = a + bL cannot be directly compared to a model with a response variable logW using the correlation or the standard error of the residuals, because the scales differ. How would you evaluate your transformed model in Exhibit 5-4 to see if it is an improvement over the linear model?
Biological theory suggests that the relationship between the weight of these animals and their wing length is exponential, i.e. W = α(10)βL, or W = α(e)βL where W is the wing weight and L is the wing length.

The model W = a + bL cannot be directly compared to a model with a response variable logW using the correlation or the standard error of the residuals, because the scales differ. How would you evaluate your transformed model in Exhibit 5-4 to see if it is an improvement over the linear model?

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck



