Deck 7: Random Variables and Discrete Probability Distributions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/55
Play
Full screen (f)
Deck 7: Random Variables and Discrete Probability Distributions
1
Which of the following best describes a function that assigns a numerical value to each simple event in a sample space? 

C
2
The Poisson random variable is a: 

A
3
Which of the following is not a characteristic of a binomial experiment? 

B
4
If X and Y are two independent random variables with V(X) = 6 and V(Y) = 5, then V(3X + 2Y) is: 


Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
5
The number of accidents that occur annually on a busy stretch of highway is an example of: 


Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
6
A table, formula, or graph that shows all possible countable values a random variable can assume, together with their associated probabilities, is called a: 


Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
7
A binomial distribution for which the number of trials n is large can well be approximated by a Poisson distribution when the probability of success, p, is: 


Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
8
The standard deviation of a binomial distribution for which n = 100 and p = .35 is: 


Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
9
Given that X is a binomial random variable, the binomial probability P(X 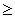 x) is approximated by the area under a normal curve to the right of:
x) is approximated by the area under a normal curve to the right of: 
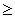 x) is approximated by the area under a normal curve to the right of:
x) is approximated by the area under a normal curve to the right of: 

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
10
If X and Y are any random variables with E(X)= 3, E(Y) = 2, E(XY) = 12, V(X) = 16 and V(Y) = 25, then the relationship between X and Y is a: Hint: corr(X,Y) =( E(xy) - E(x)E(y))/ 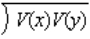



Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
11
Which of the following best describes a discrete random variable? 


Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
12
The expected value, E(X), of a binomial probability distribution is: 


Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
13
Which probability distribution is appropriate when the events of interest occur randomly, independently of one another, and rarely? 


Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
14
The weighted average of the possible values that a random variable X can assume, where the weights are the probabilities of occurrence of those values, is referred to as the: 


Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
15
The lottery commission has designed a new instant lottery game. Players pay $1.00 to scratch a ticket, where the prize won, X, (measured in $) has the following discrete probability distribution :  Which of the following best describes the expected value of X ?
Which of the following best describes the expected value of X ? 
 Which of the following best describes the expected value of X ?
Which of the following best describes the expected value of X ? 

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
16
The expected number of heads in 90 tosses of an unbiased coin is: 


Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
17
If X and Y are random variables with E(X) =7 and E(Y) = 3, then E(2X + 3Y) is: 


Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
18
The following table is a valid probability distribution, for a random variable X, where the individual probabilities are unknown.  Which of the following statements is correct ?
Which of the following statements is correct ? 
 Which of the following statements is correct ?
Which of the following statements is correct ? 

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
19
Which of the following cannot generate a Poisson distribution? 


Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
20
A Poisson distribution with = .60 is a:

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
21
State whether or not each of the following are valid probability distributions, and if not, explain why not. 


Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
22
For each of the following random variables, indicate whether the variable is discrete or continuous, and specify the possible values that it can assume.
a. X = The number of animals visited by a veterinarian in one day.
b. X = Closing share price of a particular stock over one month.
c. X = The weights of new members at a gymnasium.
d. X = The number of students attending a lecture, where the theatre seats 250 people.
e. X = The temperature at a seaside resort in the summer.
a. X = The number of animals visited by a veterinarian in one day.
b. X = Closing share price of a particular stock over one month.
c. X = The weights of new members at a gymnasium.
d. X = The number of students attending a lecture, where the theatre seats 250 people.
e. X = The temperature at a seaside resort in the summer.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
23
The lottery commission has designed a new instant lottery game. Players pay $1.00 to scratch a ticket, where the prize won, X, (measured in $) has the following discrete probability distribution :  Which of the following best describes the standard deviation of X ?
Which of the following best describes the standard deviation of X ? 
 Which of the following best describes the standard deviation of X ?
Which of the following best describes the standard deviation of X ? 

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
24
Let X and Y be two independent random variables with the following probability distributions:  Find the probability distribution of the random variable X + Y.
Find the probability distribution of the random variable X + Y.
 Find the probability distribution of the random variable X + Y.
Find the probability distribution of the random variable X + Y.
Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
25
A bivariate distribution is a distribution is a joint probability distribution of two variables.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
26
Suppose that customers arrive at a drive-through window at an average rate of three customers per minute and that their arrival follows the Poisson model.
A) Write the probability density function of the distribution of the time that will elapse before the next customer arrives.
B) Use the appropriate exponential distribution to find the probability that the next customer will arrive within 1.5 minutes.
C) Use the appropriate exponential distribution to find the probability that the next customer will not arrive within the next 2 minutes.
D) Use the appropriate Poisson distribution to answer part (c).
A) Write the probability density function of the distribution of the time that will elapse before the next customer arrives.
B) Use the appropriate exponential distribution to find the probability that the next customer will arrive within 1.5 minutes.
C) Use the appropriate exponential distribution to find the probability that the next customer will not arrive within the next 2 minutes.
D) Use the appropriate Poisson distribution to answer part (c).

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
27
A discrete random variable can take either finite or infinite values as long as the values are countable.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
28
The probability distribution for X is as follows: ![The probability distribution for X is as follows: a. Find E[5X + 1]. b. Find V[5X + 1].](https://d2lvgg3v3hfg70.cloudfront.net/TB5761/11eb16a8_bd31_dbcf_984d_0b5afae440f2_TB5761_00.jpg) a. Find E[5X + 1].
a. Find E[5X + 1].
b. Find V[5X + 1].
![The probability distribution for X is as follows: a. Find E[5X + 1]. b. Find V[5X + 1].](https://d2lvgg3v3hfg70.cloudfront.net/TB5761/11eb16a8_bd31_dbcf_984d_0b5afae440f2_TB5761_00.jpg) a. Find E[5X + 1].
a. Find E[5X + 1].b. Find V[5X + 1].

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
29
The probability distribution for X is as follows: 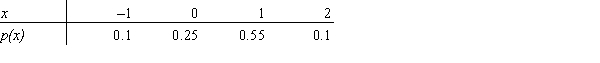 Find the expected value of Y = X + 10.
Find the expected value of Y = X + 10.
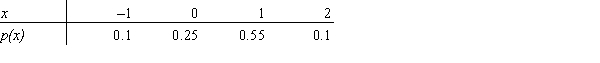 Find the expected value of Y = X + 10.
Find the expected value of Y = X + 10.
Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
30
Let X represent the number of computers in an Australian household, for those that own a computer. 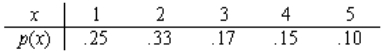 a. Find and interpret the expected number of computers in a randomly selected Australian household.
a. Find and interpret the expected number of computers in a randomly selected Australian household.
b. Find the variance of the number of computers in a randomly selected Australian household.
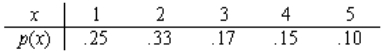 a. Find and interpret the expected number of computers in a randomly selected Australian household.
a. Find and interpret the expected number of computers in a randomly selected Australian household.b. Find the variance of the number of computers in a randomly selected Australian household.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
31
The Binomial distribution and the Poisson distribution are discrete bivariate distributions.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
32
Let X and Y be two independent random variables with the following probability distributions: a. Find the probability distribution of the random variable XY.
b. Check whether E(XY) = E(X) ´ E(Y) by separately evaluating each side of the equality.
b. Check whether E(XY) = E(X) ´ E(Y) by separately evaluating each side of the equality.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
33
Let X represent the number of computers in Australian households who own computers. The probability distribution of X is as follows: 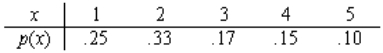 What is the probability that a randomly selected Australian household will have:
What is the probability that a randomly selected Australian household will have:
a. more than 2 computers?
b. between 2 and 5 computers, inclusive?
c. fewer than 3 computers?
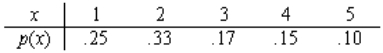 What is the probability that a randomly selected Australian household will have:
What is the probability that a randomly selected Australian household will have:a. more than 2 computers?
b. between 2 and 5 computers, inclusive?
c. fewer than 3 computers?

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
34
The probability distribution for X ,daily demand of a particular newspaper at a local newsagency,( in hundreds) is as follows: a. Find and interpret the expected value of X.
b. Find V(X).
c. Find .
b. Find V(X).
c. Find .

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
35
For a discrete probability distribution to be valid, the probabilities must lie between 0 and 1, where the sum of all probabilities must be 1.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
36
The number of people winning a lottery ticket each week is an example of a Poisson variable.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
37
The P(X ≤ x) is an example of a cumulative probability.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
38
The joint probability distribution of X and Y is shown in the following table. 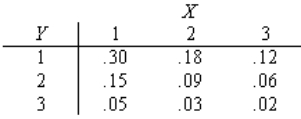 a. Determine the marginal probability distributions of X and Y.
a. Determine the marginal probability distributions of X and Y.
b. Are X and Y independent? Explain.
c. Find P(Y = 2 | X = 1).
d. Find the probability distribution of the random variable X + Y.
e. Find E(XY).
f. Find COV(X, Y).
 a. Determine the marginal probability distributions of X and Y.
a. Determine the marginal probability distributions of X and Y.b. Are X and Y independent? Explain.
c. Find P(Y = 2 | X = 1).
d. Find the probability distribution of the random variable X + Y.
e. Find E(XY).
f. Find COV(X, Y).

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
39
A Bernoulli trial is where each trial of an experiment has four possible outcomes, the probability of success is p and the trials are not independent.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
40
Gender is an example of a continuous random variable.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
41
An advertising executive receives an average of 10 telephone calls each afternoon between 2 and 4pm. The calls occur randomly and independently of one another.
a. Find the probability that the executive will receive 13 calls between 2 and 4pm on a particular afternoon.
b. Find the probability that the executive will receive seven calls between 2 and 3pm on a particular afternoon.
c. Find the probability that the executive will receive at least five calls between 2 and 4pm on a particular afternoon.
a. Find the probability that the executive will receive 13 calls between 2 and 4pm on a particular afternoon.
b. Find the probability that the executive will receive seven calls between 2 and 3pm on a particular afternoon.
c. Find the probability that the executive will receive at least five calls between 2 and 4pm on a particular afternoon.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
42
A market researcher selects 20 students at random to participate in a wine-tasting test. Each student is blindfolded and asked to take a drink out of each of two glasses, one containing an expensive wine and the other containing a cheap wine. The students are then asked to identify the more expensive wine. If the students have no ability whatsoever to discern the more expensive wine, what is the probability that the more expensive wine will be correctly identified by:
a. more than half of the students?
b. none of the students?
c. all of the students?
d. eight of the students?
a. more than half of the students?
b. none of the students?
c. all of the students?
d. eight of the students?

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
43
Let X be a Poisson random variable with = 6. Use the table of Poisson probabilities to find:
a. P(X 8)
b. P(X = 8)
c. P(X 5)
d. P(6 X 10)
a. P(X 8)
b. P(X = 8)
c. P(X 5)
d. P(6 X 10)

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
44
Let X be a binomial random variable with n = 25 and p = 0.01.
a. Use the binomial table to find P(X = 0), P(X = 1), and P(X = 2).
b. Approximate the three probabilities in part (a) using the appropriate Poisson distribution.
c. Compare your approximations in part (b) with the exact probabilities found in part (a). What is your conclusion?
a. Use the binomial table to find P(X = 0), P(X = 1), and P(X = 2).
b. Approximate the three probabilities in part (a) using the appropriate Poisson distribution.
c. Compare your approximations in part (b) with the exact probabilities found in part (a). What is your conclusion?

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
45
An analysis of the stock market produces the following information about the returns of two stocks:
Assume that the returns are positively correlated, with 12 = 0.80.
a. Find the mean and standard deviation of the return on a portfolio consisting of an equal investment in each of the two stocks.
b. Suppose that you wish to invest $1 million. Discuss whether you should invest your money in stock 1, stock 2, or a portfolio composed of an equal amount of investments on both stocks.
Assume that the returns are positively correlated, with 12 = 0.80.
a. Find the mean and standard deviation of the return on a portfolio consisting of an equal investment in each of the two stocks.
b. Suppose that you wish to invest $1 million. Discuss whether you should invest your money in stock 1, stock 2, or a portfolio composed of an equal amount of investments on both stocks.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
46
The proprietor of a small hardware store employs three men and three women. He will select three employees at random to work on Christmas Eve. Let X represent the number of women selected.
a. Express the probability distribution of X in tabular form.
b. What is the probability that at least two women will work on Christmas Eve?
a. Express the probability distribution of X in tabular form.
b. What is the probability that at least two women will work on Christmas Eve?

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
47
A recent survey in Victoria revealed that 60% of the vehicles travelling on highways, where speed limits are posted at 100 kilometres per hour, were exceeding the limit. Suppose you randomly record the speeds of 10 vehicles travelling on the Hume Highway, where the speed limit is 100 kilometres per hour. Let X denote the number of vehicles that were exceeding the limit. Find the following probabilities.
a. P(X = 10).
b. P(4 < X < 9).
c. P(X = 2).
d. P(3 X 6).
a. P(X = 10).
b. P(4 < X < 9).
c. P(X = 2).
d. P(3 X 6).

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
48
An official from the Australian Securities and Investments Commission estimates that 75% of all investment bankers have profited from the use of insider information. If 15 investment bankers are selected at random from the Commission's registry, find the probability that:
a. at most 10 have profited from insider information.
b. at least six have profited from insider information.
c. all 15 have profited from insider information.
a. at most 10 have profited from insider information.
b. at least six have profited from insider information.
c. all 15 have profited from insider information.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
49
Consider a binomial random variable X with n = 7 and p = 0.3.
a. Find the probability distribution of X.
b. Find P(X < 3).
c. Find the mean and the variance of X.
a. Find the probability distribution of X.
b. Find P(X < 3).
c. Find the mean and the variance of X.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
50
Let X be a Poisson random variable with = 8. Use the table of Poisson probabilities to find:
a. P(X 6).
b. P(X = 4).
c. P(X 3).
d. P(9 X 14).
a. P(X 6).
b. P(X = 4).
c. P(X 3).
d. P(9 X 14).

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
51
The number of arrivals at a local petrol station between 3:00 and 5:00pm has a Poisson distribution with a mean of 12.
a. Find the probability that the number of arrivals between 3:00 and 5:00pm is at least 10.
b. Find the probability that the number of arrivals between 3:30 and 4:00pm is at least 10.
c. Find the probability that the number of arrivals between 4:00 and 5:00pm is exactly two.
a. Find the probability that the number of arrivals between 3:00 and 5:00pm is at least 10.
b. Find the probability that the number of arrivals between 3:30 and 4:00pm is at least 10.
c. Find the probability that the number of arrivals between 4:00 and 5:00pm is exactly two.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
52
Given a binomial random variable with n =15 and p = 0.40, find the exact probabilities of the following events and their normal approximations.
a. X = 6.
b. X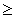 9.
9.
c. X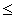 10.
10.
a. X = 6.
b. X
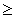 9.
9.c. X
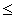 10.
10.
Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
53
Given a binomial random variable with n = 20 and p = 0.6, find the following probabilities using the binomial table.
a. P(X 13).
b. P(X 15).
c. P(X = 17).
d. P(11 < X < 14).
a. P(X 13).
b. P(X 15).
c. P(X = 17).
d. P(11 < X < 14).

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
54
Phone calls arrive at the rate of 30 per hour at the reservation desk for a hotel.
a. Find the probability of receiving two calls in a five-minute interval of time.
b. Find the probability of receiving exactly eight calls in 15 minutes.
c. If no calls are currently being processed, what is the probability that the desk employee can take a four-minute break without being interrupted?
a. Find the probability of receiving two calls in a five-minute interval of time.
b. Find the probability of receiving exactly eight calls in 15 minutes.
c. If no calls are currently being processed, what is the probability that the desk employee can take a four-minute break without being interrupted?

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
55
Historical data collected at the Commonwealth Bank in Sydney revealed that 80% of all customers applying for a loan are accepted. Suppose that 50 new loan applications are selected at random.
a. Find the expected value and the standard deviation of the number of loans that will be accepted by the bank.
b. What is the probability that at least 42 loans will be accepted?
c. What is the probability that the number of loans rejected is between 10 and 15, inclusive?
a. Find the expected value and the standard deviation of the number of loans that will be accepted by the bank.
b. What is the probability that at least 42 loans will be accepted?
c. What is the probability that the number of loans rejected is between 10 and 15, inclusive?

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck



