Deck 21: Dynamic Programming
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/38
Play
Full screen (f)
Deck 21: Dynamic Programming
1
Dynamic programming, when used for the shortest route problem, requires complete enumeration of paths from the beginning to ending node.
False
2
Finding the optimal solution to each stage of a dynamic programming problem will always lead to an optimal solution to the total problem.
True
3
In a production and inventory control problem, the states can correspond to the amount of inventory on hand at the beginning of each period.
True
4
The solution of stage k of a dynamic programming problem is dependent upon the solution of stage k−1.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
5
The stage transformation function identifies which state one reaches at the next stage for a given decision.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
6
Stage transformation functions
A) are linear.
B) calculate the return.
C) determine the output of the stage.
D) All of the alternatives are true.
A) are linear.
B) calculate the return.
C) determine the output of the stage.
D) All of the alternatives are true.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
7
State variables are a function of a state variable and a decision.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
8
In a knapsack problem, if one adds another item, one must completely resolve the problem in order to find a new optimal solution.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
9
State variables in a shortest route problem represent
A) decisions.
B) locations in the network.
C) the minimum distance between nodes.
D) None of the alternatives is true.
A) decisions.
B) locations in the network.
C) the minimum distance between nodes.
D) None of the alternatives is true.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
10
Dynamic programming is a general approach rather than a specific technique.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
11
Dynamic programming is a general approach with stage decision problems differing substantially from application to application.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
12
The subscripts used in dynamic programming notation refer to states.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
13
The stage transformation function
A) transforms the input into the output.
B) transforms a stage into a state.
C) is a different function for each stage.
D) None of the alternatives is true.
A) transforms the input into the output.
B) transforms a stage into a state.
C) is a different function for each stage.
D) None of the alternatives is true.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
14
The output of stage k is the input for stage k−1.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
15
In solving a shortest route problem using dynamic programming the stages represent how many arcs you are from the terminal node.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
16
Dynamic programming requires that its subproblems be independent of one another.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
17
In order to use dynamic programming, one must be able to view the problem as a multistage decision problem.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
18
Stages of a dynamic programming solution procedure
A) represent parts of a large mathematical model.
B) often represent a sequence of decisions made over time.
C) are usually not independent of each other.
D) All of the alternatives are true.
A) represent parts of a large mathematical model.
B) often represent a sequence of decisions made over time.
C) are usually not independent of each other.
D) All of the alternatives are true.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
19
Dynamic programming must only involve a finite number of decision alternatives and a finite number of stages.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
20
The return function for a shortest route problem refers to two directional arcs between nodes.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
21
Ajax Sound is in the business of fabricating printer connection cables. They purchase 30 foot spools of wire from National Electric at $3.00 per spool and cut the wire into various lengths.
Each length of wire is fitted with printer connector jacks at both ends and then packaged. The printer connector jacks cost $.40 per pair (one pair is used in each cable package). Packaging and labor together cost $.20 per package.
Because of Ajax's superior marketing skills they are in the enviable position of being able to sell all the printer connection cables they produce. They are currently contemplating offering four different sized cable packages:
 If unused wire from a spool can be sold for scrap at $.03 per foot, how many packages of each size cable should Ajax make from a 30-foot spool?
If unused wire from a spool can be sold for scrap at $.03 per foot, how many packages of each size cable should Ajax make from a 30-foot spool?
Each length of wire is fitted with printer connector jacks at both ends and then packaged. The printer connector jacks cost $.40 per pair (one pair is used in each cable package). Packaging and labor together cost $.20 per package.
Because of Ajax's superior marketing skills they are in the enviable position of being able to sell all the printer connection cables they produce. They are currently contemplating offering four different sized cable packages:
 If unused wire from a spool can be sold for scrap at $.03 per foot, how many packages of each size cable should Ajax make from a 30-foot spool?
If unused wire from a spool can be sold for scrap at $.03 per foot, how many packages of each size cable should Ajax make from a 30-foot spool?
Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
22
The knapsack problem is to determine how many units of each item to place in the knapsack to:
A) minimize total value.
B) maximize total value.
C) minimize the number of items in the knapsack.
D) maximize the number of items in the knapsack.
A) minimize total value.
B) maximize total value.
C) minimize the number of items in the knapsack.
D) maximize the number of items in the knapsack.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
23
Define the following terms as they relate to dynamic programming.
a.Stage
b.State variable
c.Stage transformation function
a.Stage
b.State variable
c.Stage transformation function

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
24
What is the Principle of Optimality, and what is its relationship to dynamic programming?

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
25
If x3 = t4(x4,d4) = x4 − 2d4 and r4(x4,d4) = 16d4, the subscripts refer to
A) state.
B) stage.
C) transformation.
D) return.
A) state.
B) stage.
C) transformation.
D) return.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
26
Find the shortest path through the following network using dynamic programming. 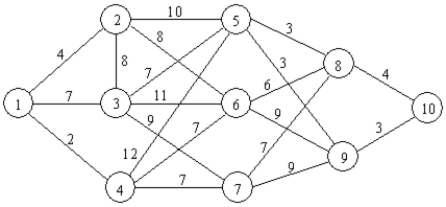


Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
27
Explain the divide-and-conquer solution strategy of dynamic programming.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
28
Solutions in dynamic programming
A) are not optimal.
B) are unique.
C) represent each stage.
D) All of the alternatives are true.
A) are not optimal.
B) are unique.
C) represent each stage.
D) All of the alternatives are true.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
29
A stage in a dynamic programming problem is defined when 2 variables and 2 functions related to that stage are defined. Identify and define the 2 variables and 2 functions and illustrate them with an example of your choice.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
30
A cargo company has a set of delivery patterns for its goods from its locations at city1 to a series of cities 2,3,4,5, and 6. The delivery times between cities are given I hours below. Find the shortest route. 


Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
31
Consider the following integer linear program
Max
5x1 + 7x2 + 9x3
s.t.
2x1 + 3x2 + 4x3 ≤ 8
x1 ≤ 3
x2 ≤ 2
x1, x2, x3 ≥ 0, integer
a.Set up the network that represents the dynamic programming formulation.
b.Solve the problem using dynamic programming.
Max
5x1 + 7x2 + 9x3
s.t.
2x1 + 3x2 + 4x3 ≤ 8
x1 ≤ 3
x2 ≤ 2
x1, x2, x3 ≥ 0, integer
a.Set up the network that represents the dynamic programming formulation.
b.Solve the problem using dynamic programming.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
32
If x3 = t4 (x4,d4) = x4 − 2d4 and r4(x4,d4) = 16d4 the state variable is
A) t
B) x
C) r
D) d
A) t
B) x
C) r
D) d

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
33
A return function is a value such as profit or loss associated with making decision dn at:
A) stage n for specific value of output variable xn.
B) stage n for a specific value of input variable xn.
C) stage n for a specific value of stage m.
D) input n for a specific value of output variable xn.
A) stage n for specific value of output variable xn.
B) stage n for a specific value of input variable xn.
C) stage n for a specific value of stage m.
D) input n for a specific value of output variable xn.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
34
Marvelous Marvin is planning his annual "Almost Everything Must Go" inventory clearance sale. Marvin has decided to allocate 18 shelf feet to the cooking section. He is considering offering up to five items for sale in this category:
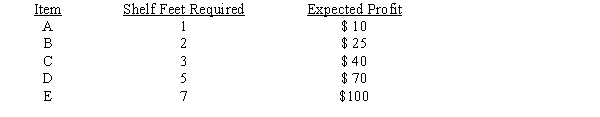
If Marvin wants at least one item A and one item B on sale, what stock should he have on sale and what is the total expected profit?
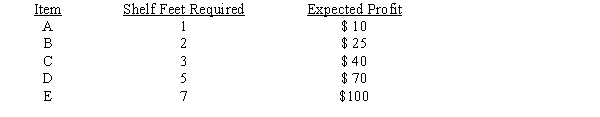
If Marvin wants at least one item A and one item B on sale, what stock should he have on sale and what is the total expected profit?

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
35
A driver wants to make a trip from city 1 to city 7. The road mileage between cities is given below. Find the shortest route. 


Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
36
If x3 = t4(x4,d4) = x4 − 2d4 and r4(x4,d4) = 16d4, the stage transformation function is
A) t
B) x
C) r
D) d
A) t
B) x
C) r
D) d

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
37
Unidyde Corporation is currently planning the production of red dye number 56 for the next four months. Production and handling costs, as well as production and storage capacity, vary from month to month. This data is given in the table below.
Production and holding costs are in ($1,000's per batch) and production levels and storage capacities are in batches. Holding costs are based on inventory on hand at the end of the month. The number of orders for batches the sales department has received over the four-month period are also given.

Unidyne does not wish to have any inventory of the dye at the end of May. Its current inventory is 2 batches. Determine a production schedule for the next four months.
Production and holding costs are in ($1,000's per batch) and production levels and storage capacities are in batches. Holding costs are based on inventory on hand at the end of the month. The number of orders for batches the sales department has received over the four-month period are also given.

Unidyne does not wish to have any inventory of the dye at the end of May. Its current inventory is 2 batches. Determine a production schedule for the next four months.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
38
We have a number of types of items to be shipped as cargo. The total available weight in the truck is ten tons. We wish to determine the number of units of items to be shipped to maximize profit. 


Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck



