Deck 9: Design of Experiments and Analysis of Variance
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/87
Play
Full screen (f)
Deck 9: Design of Experiments and Analysis of Variance
1
In a study to determine the least amount of time necessary to clean an SUV while maintaining a high quality standard, the owner of a chain of car washes designed an experiment where 20 employees were divided into four groups, each with five members. Each member of each group was assigned an SUV to clean within a certain time limit. The time limits for the groups were 20
Minutes, 25 minutes, 30 minutes, and 35 minutes. After the time limits for each group had expired, the owner inspected each SUV and rated the quality of the cleaning job on a scale of 1 to 10. What are the possible values of the response variable?
A) the time limits: 20 min, 25 min, 30 min, 35 min
B) the quality ratings: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
C) the number of employees in each group: 5
D) the number of groups: 4
Minutes, 25 minutes, 30 minutes, and 35 minutes. After the time limits for each group had expired, the owner inspected each SUV and rated the quality of the cleaning job on a scale of 1 to 10. What are the possible values of the response variable?
A) the time limits: 20 min, 25 min, 30 min, 35 min
B) the quality ratings: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
C) the number of employees in each group: 5
D) the number of groups: 4
the quality ratings: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
2
307 diamonds were sampled and randomly sorted into three groups of diamonds. These diamonds were randomly assigned to one of the three organizations, or groups (HRD, GIA, or IGI), that certify the appraisal of diamonds. A study was conducted to determine if the average size of
Diamonds reported by these three certification groups differ. A completely randomized design was used and the resulting ANOVA table is shown below. Find the F-value that is missing in the ANOVA table.
A) 0.5242
B) 83.215
C) 0.5000
D) 0.0120
Diamonds reported by these three certification groups differ. A completely randomized design was used and the resulting ANOVA table is shown below. Find the F-value that is missing in the ANOVA table.
A) 0.5242
B) 83.215
C) 0.5000
D) 0.0120
83.215
3
A scientist is hoping to compare the mean levels of DDT toxin found in three species of fish in a local river. He randomly samples 50 of each species to use in the analysis. For each fish, he measures the amount of DDT toxin present. Ideally he will be able to rank the species based on the mean level of toxin found in each of the three species. Identify the response variable in this study.
A) The amount of DDT in a fish
B) The three fish species
C) The scientist
D) The number of fish
A) The amount of DDT in a fish
B) The three fish species
C) The scientist
D) The number of fish
The amount of DDT in a fish
4
An appliance manufacturer is interested in determining whether the brand of laundry detergent used affects the average amount of dirt removed from standard household laundry loads. An experiment is set up in which 10 laundry loads are randomly assigned to each of four laundry detergents-Brands A, B, C, and D (a total of 40 loads in the experiment). The amount of dirt removed, y, (measured in milligrams) for each load is recorded and subjected to an ANOVA analysis, including a follow-up Tukey analysis. Which of the following inferences concerning the Tukey results below is incorrect?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
5
Four brands of baseball bats were tested to determine which bat allowed hitters to hit a baseball farthest. Eight different batters were thrown 25 pitches while hitting with each of the four bats (assigned in random order). The average distance of the five longest hits using each bat is shown in
The table below. The goal is to determine if the average hit distance differs for the four brands of baseball bats.
Find the F-value in the table above for testing whether the average distance hit for the four brands of baseball bats differ.
A) 39.7
B) 23.9
C) 57.6
D) 2.8
The table below. The goal is to determine if the average hit distance differs for the four brands of baseball bats.
Find the F-value in the table above for testing whether the average distance hit for the four brands of baseball bats differ.
A) 39.7
B) 23.9
C) 57.6
D) 2.8

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
6
An economist is investigating the impact of today's economy on workers in the manufacturing industry who have been laid off. A sample of 50 workers was randomly selected from all workers in manufacturing that have been laid off in the past year. The following variables were measured for each laid off worker: length of time jobless (number of weeks) and tax status (single, married, or married/head of household). The data for the 50 workers were entered into the computer and analyzed to determine if the mean number of weeks jobless differed for the three tax status groups.
The Tukey multiple comparison printout is shown below:
Tukey HSD All-Pairwise Comparisons Test of JOBLESS by STATUS
Alpha 0.1 Critical Q Value Give the population mean(s) which are in the statistically smallest group.
A) µMarried & µSingle
B) µMar/Head
C) µMarried
D) µSingle
The Tukey multiple comparison printout is shown below:
Tukey HSD All-Pairwise Comparisons Test of JOBLESS by STATUS
Alpha 0.1 Critical Q Value Give the population mean(s) which are in the statistically smallest group.
A) µMarried & µSingle
B) µMar/Head
C) µMarried
D) µSingle

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
7
In a study to determine the least amount of time necessary to clean an SUV while maintaining a high quality standard, the owner of a chain of car washes designed an experiment where 20 employees were divided into four groups, each with five members. Each member of each group was assigned an SUV to clean within a certain time limit. The time limits for the groups were 20 minutes, 25 minutes, 30 minutes, and 35 minutes. After the time limits for each group had expired, the owner inspected each SUV and rated the quality of the cleaning job on a scale of 1 to 10. What are the factor levels for this study?
A) the time limits: 20 min, 25 min, 30 min, 35 min
B) the number of employees in each group: 5
C) the quality ratings: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
D) the number of groups: 4
A) the time limits: 20 min, 25 min, 30 min, 35 min
B) the number of employees in each group: 5
C) the quality ratings: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
D) the number of groups: 4

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
8
Four brands of baseball bats were tested to determine which bat allowed hitters to hit a baseball farthest. Eight different batters were thrown 25 pitches while hitting with each of the four bats (assigned in random order). The average distance of the five longest hits using each bat is shown in the table below. The goal is to determine if the average hit distance differs for the four brands of baseball bats. Identify the response variable in this experiment.
A) The average distance hit
B) The brand of bat
C) The brand of baseball
D) A batter
A) The average distance hit
B) The brand of bat
C) The brand of baseball
D) A batter

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
9
A scientist is hoping to compare the mean levels of DDT toxin found in three species of fish in a local river. He randomly samples 50 of each species to use in the analysis. For each fish, he measures the amount of DDT toxin present. Ideally he will be able to rank the species based on the mean level of toxin found in each of the three species. How many factors are present in this study?
A) 1
B) 50
C) 6
D) 3
A) 1
B) 50
C) 6
D) 3

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
10
A study was conducted to test the effectiveness of supermarket sales strategies. At one supermarket, the price level (regular, reduced price, and at cost to supermarket) and display level (normal display space, normal display space plus end-of-aisle display, and twice the normal display space) were tested to determine if they had any effect on the weekly sales of a particular supermarket product. Each of the combinations of price level and display level were put in place for a randomly selected week and the weekly sales of the product was recorded. Each combination was used three times over the course of the experiment. The results of the study are shown here: 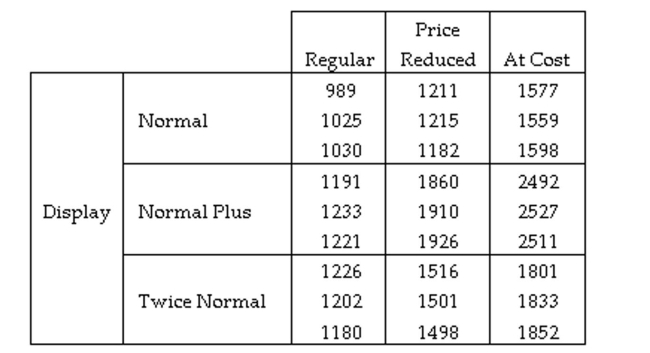 Identify the treatments used in this experiment.
Identify the treatments used in this experiment.
A) The three price levels used by the supermarket.
B) The weekly sales collected for each of the weeks.
C) The nine combinations of price level and display level used by the supermarket.
D) The three display levels used by the supermarket.
 Identify the treatments used in this experiment.
Identify the treatments used in this experiment.A) The three price levels used by the supermarket.
B) The weekly sales collected for each of the weeks.
C) The nine combinations of price level and display level used by the supermarket.
D) The three display levels used by the supermarket.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
11
Which method generally produces wider confidence intervals?
A) ANOVA
B) Tukey
C) Scheffé
D) Bonferroni
A) ANOVA
B) Tukey
C) Scheffé
D) Bonferroni

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
12
Which of the following is not a condition required for a valid ANOVA F-test for a completely randomized experiment?
A) The samples are chosen from each population in an independent manner.
B) The variances of all the sampled populations are equal.
C) The sample chosen from each of the populations is sufficiently large.
D) The sampled populations all have distributions that are approximately normal.
A) The samples are chosen from each population in an independent manner.
B) The variances of all the sampled populations are equal.
C) The sample chosen from each of the populations is sufficiently large.
D) The sampled populations all have distributions that are approximately normal.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
13
307 diamonds were sampled and randomly sorted into three groups of diamonds. These diamonds were randomly assigned to one of the three organizations, or groups (HRD, GIA, or IGI), that certify the appraisal of diamonds. A study was conducted to determine if the average size of
Diamonds reported by these three certification groups differ. A completely randomized design was used and the resulting ANOVA table is shown below.
One-Way AOV for CARAT by CERT
Specify the null hypothesis for a test to compare the mean size of a diamond for the three certification groups (HRD, GIA, and IGI).
A) At least two of the population mean carat weights differ for the three certification groups.
B) where mean carat weight for certification group i
C) , where mean carat weight.
D) , where = mean carat weight for certification group i
Diamonds reported by these three certification groups differ. A completely randomized design was used and the resulting ANOVA table is shown below.
One-Way AOV for CARAT by CERT
Specify the null hypothesis for a test to compare the mean size of a diamond for the three certification groups (HRD, GIA, and IGI).
A) At least two of the population mean carat weights differ for the three certification groups.
B) where mean carat weight for certification group i
C) , where mean carat weight.
D) , where = mean carat weight for certification group i

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
14
Which of the following is not one of the multiple comparison method options available to compare treatment means?
A) The Scheffe Method
B) The Tukey Method
C) The Einstein Method
D) The Bonferroni Method
A) The Scheffe Method
B) The Tukey Method
C) The Einstein Method
D) The Bonferroni Method

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
15
307 diamonds were sampled and randomly sorted into three groups of diamonds. These diamonds were randomly assigned to one of the three organizations, or groups (HRD, GIA, or IGI), that certify the appraisal of diamonds. A study was conducted to determine if the average size of
Diamonds reported by these three certification groups differ. A completely randomized design was used and the resulting ANOVA table is shown below.
One-Way AOV for CARAT by CERT
Give a practical conclusion for the test in the words of the problem. Use to make your conclusion.
A) There is sufficient evidence to indicate that differences exist among the mean carat weights for the three certification groups.
B) There is sufficient evidence to indicate that the mean carat weight for the HRD group equals the mean carat weight for the IGI group.
C) There is sufficient evidence to indicate that the mean carat weight for the GIA group is lower than the other two groups.
D) There is insufficient evidence to indicate that differences exist among the mean carat weights for the three certification groups.
Diamonds reported by these three certification groups differ. A completely randomized design was used and the resulting ANOVA table is shown below.
One-Way AOV for CARAT by CERT
Give a practical conclusion for the test in the words of the problem. Use to make your conclusion.
A) There is sufficient evidence to indicate that differences exist among the mean carat weights for the three certification groups.
B) There is sufficient evidence to indicate that the mean carat weight for the HRD group equals the mean carat weight for the IGI group.
C) There is sufficient evidence to indicate that the mean carat weight for the GIA group is lower than the other two groups.
D) There is insufficient evidence to indicate that differences exist among the mean carat weights for the three certification groups.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
16
A scientist is hoping to compare the mean levels of DDT toxin found in three species of fish in a local river. He randomly samples 50 of each species to use in the analysis. For each fish, he measures the amount of DDT toxin present. Ideally he will be able to rank the species based on the mean level of toxin found in each of the three species. Identify the treatments for this study.
A) The three fish species
B) The 50 fish
C) The amount of DDT in a fish
D) The scientist
A) The three fish species
B) The 50 fish
C) The amount of DDT in a fish
D) The scientist

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
17
A study was conducted to test the effectiveness of supermarket sales strategies. At one supermarket, the price level (regular, reduced price, and at cost to supermarket) and display level (normal display space, normal display space plus end-of-aisle display, and twice the normal display space) were tested to determine if they had any effect on the weekly sales of a particular supermarket product. Each of the combinations of price level and display level were put in place for a randomly selected week and the weekly sales of the product was recorded. Each combination was used three times over the course of the experiment. The results of the study are shown here: 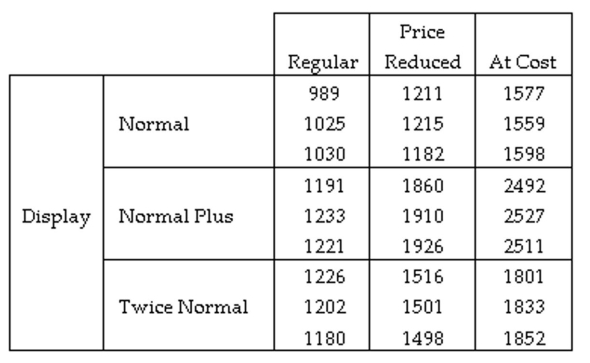
Based on the results found in the ANOVA table, should the Main Effects tests for either Display or price be conducted?
A) No. The interaction of Display and Price indicates that the Main Effects should not be tested.
B) It depends on whether the main effects tests will be significant or not.
C) Yes. The interaction of Display and Price indicates that the Main Effects should be tested.
D) Yes. The main effects tests are both significant and should be tested.

Based on the results found in the ANOVA table, should the Main Effects tests for either Display or price be conducted?
A) No. The interaction of Display and Price indicates that the Main Effects should not be tested.
B) It depends on whether the main effects tests will be significant or not.
C) Yes. The interaction of Display and Price indicates that the Main Effects should be tested.
D) Yes. The main effects tests are both significant and should be tested.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
18
A study was conducted to test the effectiveness of supermarket sales strategies. At one supermarket, the price level (regular, reduced price, and at cost to supermarket) and display level (normal display space, normal display space plus end-of-aisle display, and twice the normal display space) were tested to determine if they had any effect on the weekly sales of a particular supermarket product. Each of the combinations of price level and display level were put in place for a randomly selected week and the weekly sales of the product was recorded. Each combination was used three times over the course of the experiment. The results of the study are shown here: 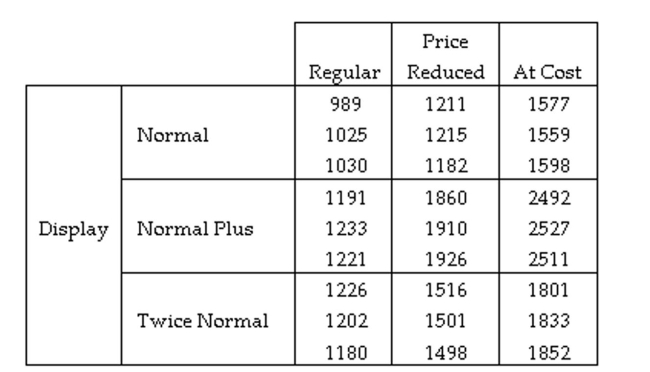 Identify the response variable used in this experiment.
Identify the response variable used in this experiment.
A) The three display levels used by the supermarket.
B) The weekly sales collected for each of the weeks.
C) The three price levels used by the supermarket.
D) The nine combinations of price level and display level used by the supermarket.
 Identify the response variable used in this experiment.
Identify the response variable used in this experiment.A) The three display levels used by the supermarket.
B) The weekly sales collected for each of the weeks.
C) The three price levels used by the supermarket.
D) The nine combinations of price level and display level used by the supermarket.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
19
Which procedure was specifically developed for pairwise comparisons when the sample sizes of the treatments are equal?
A) ANOVA
B) Tukey
C) Bonferroni
D) Scheffé
A) ANOVA
B) Tukey
C) Bonferroni
D) Scheffé

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
20
A study was conducted to test the effectiveness of supermarket sales strategies. At one supermarket, the price level (regular, reduced price, and at cost to supermarket) and display level (normal display space, normal display space plus end-of-aisle display, and twice the normal display space) were tested to determine if they had any effect on the weekly sales of a particular supermarket product. Each of the combinations of price level and display level were put in place for a randomly selected week and the weekly sales of the product was recorded. Each combination was used three times over the course of the experiment. The results of the study are shown here: 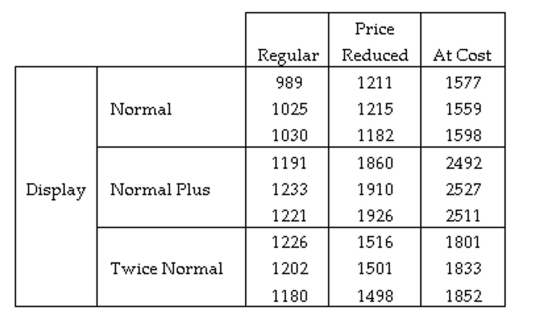
Which of the following tests should be conducted first?
A) A test of the Display Main Effect.
B) A test of the Weekly Sales Main Effect.
C) A test of the Price Main Effect.
D) A test of the interaction between Price and Display.

Which of the following tests should be conducted first?
A) A test of the Display Main Effect.
B) A test of the Weekly Sales Main Effect.
C) A test of the Price Main Effect.
D) A test of the interaction between Price and Display.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
21
A study was conducted to test the effectiveness of supermarket sales strategies. At one supermarket, the price level (regular, reduced price, and at cost to supermarket) and display level (normal display space, normal display space plus end-of-aisle display, and twice the normal display space) were tested to determine if they had any effect on the weekly sales of a particular supermarket product. Each of the combinations of price level and display level were put in place for a randomly selected week and the weekly sales of the product was recorded. Each combination was used three times over the course of the experiment. The results of the study are shown here: 
Find the test statistic for determining whether the interaction between Price and Display is significant.
A) 1709.37
B) 3121.89
C) 495
D) 257.93

Find the test statistic for determining whether the interaction between Price and Display is significant.
A) 1709.37
B) 3121.89
C) 495
D) 257.93

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
22
In a completely randomized design experiment, 10 experimental units were randomly chosen for each of three treatment groups and a quantity was measured for each unit within each group. In the first steps of testing whether the means of the three groups are the same, the sum of squares for treatments was calculated to be 3,110 and the sum of squares for error was calculated to be 27,000.
Complete the ANOVA table.
Complete the ANOVA table.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
23
Psychologists have found that people are generally reluctant to transmit bad news to their peers. This phenomenon has been named the "MUM effect." To investigate the cause of the MUM effect, 40 undergraduates at a university participated in an experiment. Each subject was asked to administer an IQ test to another student and then provide the test taker with his or her percentile score. (Unknown to the subject, the test taker was a bogus student who
was working with the researchers.) The experimenters manipulated two factors, subject visibility and success of test taker, each at two levels. Subject visibility was either visible or not visible to the test taker. Success of test taker was either top 20% or bottom 20%. Ten subjects were randomly assigned to each of the 2 x 2 4 experimental conditions, then the time (in seconds) between the end of the test and the delivery of the percentile score from the subject to the test taker was measured. (This variable is called the latency to feedback.)
The data was subject to an analysis of variance, with the following results:
Is there evidence to indicate that subject visibility and test taker success interact?
was working with the researchers.) The experimenters manipulated two factors, subject visibility and success of test taker, each at two levels. Subject visibility was either visible or not visible to the test taker. Success of test taker was either top 20% or bottom 20%. Ten subjects were randomly assigned to each of the 2 x 2 4 experimental conditions, then the time (in seconds) between the end of the test and the delivery of the percentile score from the subject to the test taker was measured. (This variable is called the latency to feedback.)
The data was subject to an analysis of variance, with the following results:
Is there evidence to indicate that subject visibility and test taker success interact?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
24
Find the critical value F0 for a one-tailed test using  with 8 numerator degrees of freedom and 15 denominator degrees of freedom
with 8 numerator degrees of freedom and 15 denominator degrees of freedom
A) 3.20
B) 3.22
C) 4.10
D) 2.64
 with 8 numerator degrees of freedom and 15 denominator degrees of freedom
with 8 numerator degrees of freedom and 15 denominator degrees of freedomA) 3.20
B) 3.22
C) 4.10
D) 2.64

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
25
Psychologists have found that people are generally reluctant to transmit bad news to their peers. This phenomenon has been named the "MUM effect." To investigate the cause of the MUM effect, undergraduates at a university participated in an experiment. Each subject was asked to administer an IQ test to another student and then provide the test taker with his or her percentile score. (Unknown to the subject, the test taker was a bogus student who was working with the researchers.) The experimenters manipulated two factors, subject visibility and success of test taker, each at two levels. Subject visibility was either visible or not visible to the test taker. Success of test taker was either top 20% or bottom 20%. Ten subjects were randomly assigned to each of the 2 x 2 xperimental conditions. Then the time (in seconds) between the end of the test and the delivery of the percentile score from
the subject to the test taker was measured. (This variable is called the latency to feedback.)
Describe the experiment, including the response variable, factors, factor levels, replications, and treatments.
the subject to the test taker was measured. (This variable is called the latency to feedback.)
Describe the experiment, including the response variable, factors, factor levels, replications, and treatments.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
26
Four brands of baseball bats were tested to determine which bat allowed hitters to hit a baseball farthest. Eight different batters were thrown 25 pitches while hitting with each of the four bats (assigned in random order). The average distance of the five longest hits using each bat is shown in the table below. The goal is to determine if the average hit distance differs for the four brands of baseball bats.
How should the data be analyzed?
A) Completely randomized design with four treatments
B) 4 × 8 factorial design
C) Randomized block design with four treatments and eight blocks
D) Randomized block design with eight treatments and four blocks
How should the data be analyzed?
A) Completely randomized design with four treatments
B) 4 × 8 factorial design
C) Randomized block design with four treatments and eight blocks
D) Randomized block design with eight treatments and four blocks

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
27
307 diamonds were sampled and randomly sorted into three groups of diamonds. These diamonds were randomly assigned to one of the three organizations, or groups (HRD, GIA, or IGI), that certify the appraisal of diamonds. A study was conducted to determine if the average size of
Diamonds reported by these three certification groups differ. A completely randomized design was used and the Bonferroni multiple comparison results are shown below.
Bonferroni All-Pairwise Comparisons Test of CARAT by CERT
Alpha
Give the population mean(s) which are in the statistically largest group.
A) µHRD & µGIA
B) µIGI
C) µGIA
D) µHRD
Diamonds reported by these three certification groups differ. A completely randomized design was used and the Bonferroni multiple comparison results are shown below.
Bonferroni All-Pairwise Comparisons Test of CARAT by CERT
Alpha
Give the population mean(s) which are in the statistically largest group.
A) µHRD & µGIA
B) µIGI
C) µGIA
D) µHRD

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
28
A beverage distributor wanted to determine the combination of advertising agency (two levels) and advertising medium (three levels) that would produce the largest increase in sales per advertising dollar. Each of the advertising agencies prepared ads as required for each of the media-- newspaper, radio, and television. Twelve small towns of roughly the same size were selected for the experiment, and two each were randomly assigned to receive an advertisement prepared and transmitted by each of the six agency-medium
combinations. The dollar increases in sales per advertising dollar, based on a 1-month sales period, are shown in the table.
The SPSS analysis is shown below.
A N A L YSIS OF V ARIANCE***
SALES
BY AGENCY
MEDIUM
(Note: SPSS uses "Explained" instead of "Treatment" in the factorial analysis. Also, SPSS uses "Residual" instead of "Error.") Would you test the main effects factors, agency and medium, in this example? Explain why or why not.
combinations. The dollar increases in sales per advertising dollar, based on a 1-month sales period, are shown in the table.
The SPSS analysis is shown below.
A N A L YSIS OF V ARIANCE***
SALES
BY AGENCY
MEDIUM
(Note: SPSS uses "Explained" instead of "Treatment" in the factorial analysis. Also, SPSS uses "Residual" instead of "Error.") Would you test the main effects factors, agency and medium, in this example? Explain why or why not.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
29
A local consumer reporter wants to compare the average costs of grocery items purchased at three different supermarkets, A, B, and C. Prices (in dollars) were recorded for a sample of 60 randomly selected grocery items at each of the three supermarkets. In order to reduce item-to-item variation, the prices were recorded for each item on the same day at each supermarket.
The results of the Bonferroni analysis are summarized below. Fully interpret the Bonferroni analysis.
The results of the Bonferroni analysis are summarized below. Fully interpret the Bonferroni analysis.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
30
The results of a Tukey multiple comparison are summarized below.  a. How many pairwise comparisons of the three treatments are there?
a. How many pairwise comparisons of the three treatments are there?
b. Which treatments are significantly different from each other?
c. Which treatments are not significantly different from each other?
 a. How many pairwise comparisons of the three treatments are there?
a. How many pairwise comparisons of the three treatments are there?b. Which treatments are significantly different from each other?
c. Which treatments are not significantly different from each other?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
31
a. Calculate the mean response for each treatment
b. The MINITAB ANOVA printout is shown here. Test for interaction at the =0.05 level of significance.
Analysis of variance for response.
c. Does the result warrant tests of the two factor mean effects?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
32
Four brands of baseball bats were tested to determine which bat allowed hitters to hit a baseball farthest. Eight different batters were thrown 25 pitches while hitting with each of the four bats (assigned in random order). The average distance of the five longest hits using each bat is shown in the table below. The goal is to determine if the average hit distance differs for the four brands of baseball bats.
The ANOVA table output is shown here:
Based on the p-value for this test, make the proper conclusion about the treatments in this experiment.
A) There is insufficient evidence (at ) to indicate differences among the mean distances for the four brands of baseball bats.
B) There is sufficient evidence (at ) to indicate differences among the mean distances for the four brands of baseball bats.
C) There is sufficient evidence (at ) to indicate differences among the mean distances for the eight batters.
D) There is insufficient evidence (at ) to indicate differences among the mean distances for the eight batters.
The ANOVA table output is shown here:
Based on the p-value for this test, make the proper conclusion about the treatments in this experiment.
A) There is insufficient evidence (at ) to indicate differences among the mean distances for the four brands of baseball bats.
B) There is sufficient evidence (at ) to indicate differences among the mean distances for the four brands of baseball bats.
C) There is sufficient evidence (at ) to indicate differences among the mean distances for the eight batters.
D) There is insufficient evidence (at ) to indicate differences among the mean distances for the eight batters.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
33
Complete the ANOVA table.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
34
A company that employs a large number of salespeople is interested in learning which of the salespeople sell the most: those strictly on commission, those with a fixed salary, or those with a reduced fixed salary plus a commission. The previous month's records for a sample of salespeople are inspected and the amount of sales (in dollars) is recorded for each, as shown in the table.
Test to determine if a difference exists in the mean sale amounts among the three compensation systems. Test using .
Test to determine if a difference exists in the mean sale amounts among the three compensation systems. Test using .

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
35
Use the appropriate table to find the following F value: 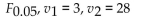
A) 2.95
B) 8.62
C) 3.34
D) 2.92
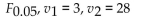
A) 2.95
B) 8.62
C) 3.34
D) 2.92

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
36
An experiment was conducted using a randomized block design. The data from the experiment are displayed in the following table.
Fill in the missing entries for an ANOVA table.
Fill in the missing entries for an ANOVA table.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
37
Complete the ANOVA table.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
38
A partially completed ANOVA table for a completely randomized design is shown here. a. Complete the ANOVA table.
b. How many treatments are involved in the experiment?
c. Do the data provide sufficient evidence to indicate a difference among the population means? Test using
b. How many treatments are involved in the experiment?
c. Do the data provide sufficient evidence to indicate a difference among the population means? Test using

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
39
Four brands of baseball bats were tested to determine which bat allowed hitters to hit a baseball farthest. Eight different batters were thrown 25 pitches while hitting with each of the four bats (assigned in random order). The average distance of the five longest hits using each bat is shown in the table below. The goal is to determine if the average hit distance differs for the four brands of baseball bats.
Identify the test statistic that should be used for testing whether the average distance hit for the four brands of baseball bats differ.
A) 23.85
B) 0.0000
C) 57.55
D) 39.7
Identify the test statistic that should be used for testing whether the average distance hit for the four brands of baseball bats differ.
A) 23.85
B) 0.0000
C) 57.55
D) 39.7

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
40
Consider a completely randomized design with five treatments. How many pairwise comparisons of treatments are made in a Bonferroni analysis?
A)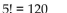
B) 10
C) 5
D) 20
A)
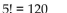
B) 10
C) 5
D) 20

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
41
Given that the mean square for treatments (MST) for an ANOVA F-test is 5,000 and the mean square for error (MSE) is 3,750, find the value of the test statistic F.
A) 1.33
B) .800
C) .750
D) 1.25
A) 1.33
B) .800
C) .750
D) 1.25

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
42
__________ is a particular combination of levels of the factors involved in a study.
A) The factor level
B) The sampling design
C) An analysis of variance
D) A treatment
A) The factor level
B) The sampling design
C) An analysis of variance
D) A treatment

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
43
Given that the sum of squares for error (SSE) for an ANOVA F-test is 12,000 and there are 40 total experimental units with eight total treatments, find the mean square for error (MSE).
A) 308
B) 300
C) 400
D) 375
A) 308
B) 300
C) 400
D) 375

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
44
A certain HMO is attempting to show the benefits of managed health care to an insurance company. The HMO believes that certain types of doctors are more cost-effective than others. One theory is that primary specialty is an important factor in measuring the cost-effectiveness of physicians. To investigate this, the HMO obtained independent random samples of 28 HMO physicians from each of four primary specialties-- General Practice (GP), Internal Medicine (IM), pediatrics (PED), and Family Physician (FP)-- and recorded the total per-member, per-month charges for each. Identify the treatments for this group.
A) the HMO
B) the four specialty groups-GP, IM, PED, and FP
C) the total per-member, per-month charges
D) the 112 physicians
A) the HMO
B) the four specialty groups-GP, IM, PED, and FP
C) the total per-member, per-month charges
D) the 112 physicians

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
45
A local consumer reporter wants to compare the average costs of grocery items purchased at three different supermarkets, A, B, and C. Prices (in dollars) were recorded for a sample of 60 randomly selected grocery items at each of the three supermarkets. In order to reduce item-to-item variation,
The prices were recorded for each item on the same day at each supermarket.
The results of a Bonferroni analysis are summarized below. Interpret the Bonferroni analysis results.
A) A has a significantly smaller mean price than either of the other two supermarkets.
B) C has a significantly larger mean price than either of the other two supermarkets.
C) B and C have significantly different mean prices.
D) A has a significantly larger mean price than either of the other two supermarkets.
The prices were recorded for each item on the same day at each supermarket.
The results of a Bonferroni analysis are summarized below. Interpret the Bonferroni analysis results.
A) A has a significantly smaller mean price than either of the other two supermarkets.
B) C has a significantly larger mean price than either of the other two supermarkets.
C) B and C have significantly different mean prices.
D) A has a significantly larger mean price than either of the other two supermarkets.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
46
A local consumer reporter wants to compare the average costs of grocery items purchased at three different supermarkets, A, B, and C. Prices (in dollars) were recorded for a sample of 60 randomly selected grocery items at each of the three supermarkets. In order to reduce item-to-item variation,
The prices were recorded for each item on the same day at each supermarket.
The results of the ANOVA test are summarized in the following table.
What is the value of the test statistic for determining whether the three supermarkets have the sam average prices?
A) 0.0001
B) 108.54
C) 1.3206
D) 39.23
The prices were recorded for each item on the same day at each supermarket.
The results of the ANOVA test are summarized in the following table.
What is the value of the test statistic for determining whether the three supermarkets have the sam average prices?
A) 0.0001
B) 108.54
C) 1.3206
D) 39.23

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
47
A certain HMO is attempting to show the benefits of managed care to an insurance company. The HMO believes that certain types of doctors are more cost-effective than others. One theory is that certification level is an important factor in measuring the cost-effectiveness of physicians. To investigate this, the HMO obtained independent random samples of 26 physicians from each of the three certification levels-Board certified (C); Uncertified, board eligible (E); and Uncertified, board ineligible (I)- and recorded the total per member per month charges for each (a total of 78 Physicians). How many factors are present in this study?
A) 26
B) 1
C) 3
D) 78
A) 26
B) 1
C) 3
D) 78

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
48
A local consumer reporter wants to compare the average costs of grocery items purchased at three different supermarkets, A, B, and C. Prices (in dollars) were recorded for a sample of 60 randomly selected grocery items at each of the three supermarkets. In order to reduce item-to-item variation, the prices were recorded for each item on the same day at each supermarket.
The results of the ANOVA are summarized in the following table. Based on the p-value of the test, make the proper conclusion.
A) There is sufficient evidence (at ) to indicate that the mean prices of grocery items at the three supermarkets are identical.
B) There is insufficient evidence (at ) to indicate differences among the mean prices of grocery items at the three supermarkets.
C) There is sufficient evidence (at ) to indicate differences among the mean prices of grocery items at the three supermarkets.
D) No conclusions can be drawn from the given information.
The results of the ANOVA are summarized in the following table. Based on the p-value of the test, make the proper conclusion.
A) There is sufficient evidence (at ) to indicate that the mean prices of grocery items at the three supermarkets are identical.
B) There is insufficient evidence (at ) to indicate differences among the mean prices of grocery items at the three supermarkets.
C) There is sufficient evidence (at ) to indicate differences among the mean prices of grocery items at the three supermarkets.
D) No conclusions can be drawn from the given information.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
49
A city monitors ozone levels weekly over a 3 year period in order to relate the ozone levels to the seasons. Determine whether the study is observational or designed.
A) designed
B) observational
A) designed
B) observational

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
50
Find the following: 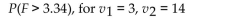
A) 0.95
B) 0.92
C) 0.03
D) 0.05
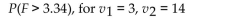
A) 0.95
B) 0.92
C) 0.03
D) 0.05

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
51
In an experiment with 10 treatments, how many pairs of means can be compared?
A) 90
B) 20
C) 100
D) 45
A) 90
B) 20
C) 100
D) 45

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
52
Psychologists have found that people are generally reluctant to transmit bad news to their peers. This phenomenon has been named the "MUM effect." To investigate the cause of the MUM effect, undergraduates at a university participated in an experiment. Each subject was asked to administer an IQ test to another student and then provide the test taker with his or her percentile score.
(Unknown to the subject, the test taker was a bogus student who was working with the researchers.) The experimenters manipulated two factors, subject visibility and success of test taker, each at two levels. Subject visibility was either visible or not visible to the test taker. Success of test taker was either top 20% or bottom 20%. Ten subjects were randomly assigned to each of the 2 4 experimental conditions. Then the time (in seconds) between the end of the test and the delivery of the percentile score from the subject to the test taker was measured. (This variable is called the latency to feedback.) What type of experimental design was employed in this study?
A) 4 x 20 factorial design with no replications
B) completely randomized design with four treatments
C) 2 x 2 factorial design with 10 replications
D) randomized block design with four treatments and 10 blocks
(Unknown to the subject, the test taker was a bogus student who was working with the researchers.) The experimenters manipulated two factors, subject visibility and success of test taker, each at two levels. Subject visibility was either visible or not visible to the test taker. Success of test taker was either top 20% or bottom 20%. Ten subjects were randomly assigned to each of the 2 4 experimental conditions. Then the time (in seconds) between the end of the test and the delivery of the percentile score from the subject to the test taker was measured. (This variable is called the latency to feedback.) What type of experimental design was employed in this study?
A) 4 x 20 factorial design with no replications
B) completely randomized design with four treatments
C) 2 x 2 factorial design with 10 replications
D) randomized block design with four treatments and 10 blocks

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
53
Define the statistical term "treatments."
A) assumptions that are satisfied exactly
B) combinations of factor-levels employed in a designed study
C) correlations among the factors used in an analysis of variance
D) objects on which the responses are measured
A) assumptions that are satisfied exactly
B) combinations of factor-levels employed in a designed study
C) correlations among the factors used in an analysis of variance
D) objects on which the responses are measured

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
54
An industrial psychologist is investigating the effects of work environment on employee attitudes. A group of 28 recently hired sales trainees were randomly assigned to one of 7 different "home rooms" - four trainees per room. Each room is identical except for wall color, with 7 different colors used. The psychologist wants to know whether room color has an effect on attitude, and, if so, wants to compare the mean attitudes of the trainees assigned to the 7 room colors. At the end of the training program, the attitude of each trainee was measured on a 100-pt. scale (the lower the score, the poorer the attitude). How many treatments are in this study?
A) 4
B) 7
C) 100
D) 28
A) 4
B) 7
C) 100
D) 28

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
55
Find the critical value 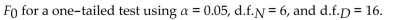
A) 3.94
B) 2.66
C) 2.74
D) 2.19
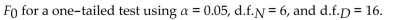
A) 3.94
B) 2.66
C) 2.74
D) 2.19

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
56
A local consumer reporter wants to compare the average costs of grocery items purchased at three different supermarkets, A, B, and C. Prices (in dollars) were recorded for a sample of 60 randomly selected grocery items at each of the three supermarkets. In order to reduce item-to-item variation, the prices were recorded for each item on the same day at each supermarket.
Identify the treatments for this experiment.
A) the three supermarkets
B) the 60 grocery items
C) the day on which the data were collected
D) the prices
Identify the treatments for this experiment.
A) the three supermarkets
B) the 60 grocery items
C) the day on which the data were collected
D) the prices

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
57
A multiple-comparison procedure for comparing four treatment means produced the confidence intervals shown below. For each pair of means, indicate which mean is larger or indicate that there is no significant difference.
A) ; no significant difference between and ; no significant difference between and
B) no significant difference between and ; no significant difference between and ; no significant difference between and
C) ; no significant difference between and ; no significant difference between and
D)
A) ; no significant difference between and ; no significant difference between and
B) no significant difference between and ; no significant difference between and ; no significant difference between and
C) ; no significant difference between and ; no significant difference between and
D)

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
58
A certain HMO is attempting to show the benefits of managed care to an insurance company. The HMO believes that certain types of doctors are more cost-effective than others. One theory is that certification level is an important factor in measuring the cost-effectiveness of physicians. To investigate this, the HMO obtained independent random samples of 30 physicians from each of the three certification levels- Board certified (C); Uncertified, board eligible (E); and Uncertified, board ineligible (I)- and recorded the total per-member, per-month charges for each (a total of 90 physicians). Identify the dependent (response) variable for this study.
A) the HMO
B) the three certifications groups- C, E, and I
C) the 90 physicians
D) the total per-member, per-month charge
A) the HMO
B) the three certifications groups- C, E, and I
C) the 90 physicians
D) the total per-member, per-month charge

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
59
Four different leadership styles used by Big-Six accountants were investigated. As part of a designed study, 15 accountants were randomly selected from each of the four leadership style groups (a total of 60 accountants). Each accountant was asked to rate the degree to which their subordinates performed substandard field work on a 10-point scale-called the "substandard work scale". The objective is to compare the mean substandard work scales of the four leadership styles.
The data on substandard work scales for all 60 observations were subjected to an analysis of variance.
ONE-WAY ANOVA FOR SUBSTAND BY STYLE
Interpret the results of the ANOVA -test shown on the printout for .
A) At , nothing can be said.
B) At , there is no evidence of interaction.
C) At , there is sufficient evidence of differences among the substandard work scale means for the four leadership styles.
D) At , there is insufficient evidence of differences among the substandard work scale means for the four leadership styles.
The data on substandard work scales for all 60 observations were subjected to an analysis of variance.
ONE-WAY ANOVA FOR SUBSTAND BY STYLE
Interpret the results of the ANOVA -test shown on the printout for .
A) At , nothing can be said.
B) At , there is no evidence of interaction.
C) At , there is sufficient evidence of differences among the substandard work scale means for the four leadership styles.
D) At , there is insufficient evidence of differences among the substandard work scale means for the four leadership styles.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
60
A multiple-comparison procedure for comparing four treatment means produced the confidence intervals shown below. Rank the means from smallest to largest. Use solid lines to connect those means which are not significantly different.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
61
Suppose an experiment utilizing a random block design has 5 treatments and 8 blocks for a total of 40 observations. Assume that the total Sum of Squares for the response is SS(Total)=300 . If the Sum of Squares for Treatments (SST) is 40 % of SS(Total), and the Sum of Squares for Blocks (SSB) is 10 % of SS (Total), find the F values for this experiment.
A) treatments: F=4.48 ; blocks: F=0.70
B) treatments: F=13.00 ; blocks: F=7.43
C) treatments: F=7.8 ; blocks: F=1.11
D) treatments: F=5.60 ; blocks: F=0.80
A) treatments: F=4.48 ; blocks: F=0.70
B) treatments: F=13.00 ; blocks: F=7.43
C) treatments: F=7.8 ; blocks: F=1.11
D) treatments: F=5.60 ; blocks: F=0.80

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
62
The randomized block design is an extension of the matched pairs comparison of µ1 and µ2.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
63
Given that the sum of squares for treatments (SST) for an ANOVA F-test is 9,000 and there are four total treatments, find the mean square for treatments (MST).
A) 1,500
B) 3,000
C) 2,250
D) 1,800
A) 1,500
B) 3,000
C) 2,250
D) 1,800

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
64
Suppose a company makes 4 different frozen dinners, and tests their ability to attract customers. They test the frozen dinners in 20 different stores in order to account for any extraneous sources of variation. The company records the number of customers who purchase each product at each store.
What assumptions are necessary for the validity of the F statistic for comparing the response meansof the 4 frozen dinners?
A) The means of the observations corresponding to all the block-treatment combinations are equal, and the variances of all the probability distributions are equal.
B) The probability distributions of observations corresponding to all the block-treatment combinations are normal, and the sampling distributions of the variances of all the
Block-treatment combinations are normally distributed.
C) The probability distributions of observations corresponding to all the block-treatment combinations are normal, and the variances of all the probability distributions are equal.
D) None. The Central Limit Theorem eliminates the need for any assumptions.
What assumptions are necessary for the validity of the F statistic for comparing the response meansof the 4 frozen dinners?
A) The means of the observations corresponding to all the block-treatment combinations are equal, and the variances of all the probability distributions are equal.
B) The probability distributions of observations corresponding to all the block-treatment combinations are normal, and the sampling distributions of the variances of all the
Block-treatment combinations are normally distributed.
C) The probability distributions of observations corresponding to all the block-treatment combinations are normal, and the variances of all the probability distributions are equal.
D) None. The Central Limit Theorem eliminates the need for any assumptions.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
65
A certain HMO is attempting to show the benefits of managed care to an insurance company. The HMO believes that certain types of doctors are more cost-effective than others. One theory is that certification level is an important factor in measuring the cost-effectiveness of physicians. To investigate this, the HMO obtained independent random samples of 21 physicians from each of the three certification levels-Board certified (C); Uncertified, board eligible (E); and Uncertified, board ineligible (I)-and recorded the total per-member, per-month charges for each (a total of 63 physicians). In order to compare the mean charges for the three groups, the data will be subjected to an analysis of variance. Give the degrees of freedom appropriate for conducting the ANOVA F-test.
A) numerator , denominator
B) numerator , denominator
C) numerator , denominator
D) numerator , denominator
A) numerator , denominator
B) numerator , denominator
C) numerator , denominator
D) numerator , denominator

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
66
A local consumer reporter wants to compare the average costs of grocery items purchased at three different supermarkets, A, B, and C. Prices (in dollars) were recorded for a sample of 60 randomly selected grocery items at each of the three supermarkets. In order to reduce item-to-item variation,
The prices were recorded for each item on the same day at each supermarket. Identify the dependent (response) variable for this experiment.
A) the mean prices of the grocery items at each supermarket
B) the prices of the grocery items
C) the grocery items
D) the supermarkets
The prices were recorded for each item on the same day at each supermarket. Identify the dependent (response) variable for this experiment.
A) the mean prices of the grocery items at each supermarket
B) the prices of the grocery items
C) the grocery items
D) the supermarkets

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
67
Find the following: 
A) 0.05
B) 0.025
C) 0.975
D) 0.95

A) 0.05
B) 0.025
C) 0.975
D) 0.95

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
68
Psychologists have found that people are generally reluctant to transmit bad news to their peers. This phenomenon has been named the "MUM effect." To investigate the cause of the MUM effect, 40 undergraduates at a certain university participated in an experiment. Each subject was asked to administer an IQ test to another student and then provide the test taker with his or her percentile score. (Unknown to the subject, the test taker was a bogus student who was working with the researchers.) The experimenters manipulated two factors, subject visibility and success of test taker, each at two levels. Subject visibility was either visible or not visible to the test taker. Success of test
Taker was either top 20% or bottom 20%. Ten subjects were randomly assigned to each of the 2 x 2 4 experimental conditions, then the time (in seconds) between the end of the test and the delivery of the percentile score from the subject to the test taker was measured. (This variable is called the latency to feedback.) The data was subject to an analysis of variance, with the following results:
Which conclusion can you draw from the analysis? Use .
A) At , there is sufficient evidence to indicate that subject visibility and test taker success interact.
B) At , neither subject visibility nor test taker success are important predictors of latency to feedback.
C) At , there is no evidence of interaction between subject visibility and test taker success.
D) At , the model is not useful for predicting latency to feedback.
Taker was either top 20% or bottom 20%. Ten subjects were randomly assigned to each of the 2 x 2 4 experimental conditions, then the time (in seconds) between the end of the test and the delivery of the percentile score from the subject to the test taker was measured. (This variable is called the latency to feedback.) The data was subject to an analysis of variance, with the following results:
Which conclusion can you draw from the analysis? Use .
A) At , there is sufficient evidence to indicate that subject visibility and test taker success interact.
B) At , neither subject visibility nor test taker success are important predictors of latency to feedback.
C) At , there is no evidence of interaction between subject visibility and test taker success.
D) At , the model is not useful for predicting latency to feedback.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
69
Consider a completely randomized design with k treatments. Assume all pairwise comparisons of treatment means are to be made using a multiple comparisons procedure. Determine the total number of treatment means to be compared for the value
A) 18
B) 36
C) 9
D) 45
A) 18
B) 36
C) 9
D) 45

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
70
An industrial psychologist is investigating the effects of work environment on employee attitudes. A group of 20 recently hired sales trainees were randomly assigned to one of four different "home rooms"- five trainees per room. Each room is identical except for wall color. The four colors used were light green, light blue, gray, and red. The psychologist wants to know whether room color has an effect on attitude, and, if so, wants to compare the mean attitudes of the trainees assigned to the four room colors. At the end of the training program, the attitude of each trainee was measured on a60-pt. scale (the lower the score, the poorer the attitude). The data was subjected to a one-way analysis of variance.
ONE-WAY ANOVA FOR ATTITUDE BY COLOR
Give the null hypothesis for the ANOVA F-test shown on the printout.
A) , where the s represent the proportion with the corresponding attitude
B) , where the s represent the room colors
C) , where the
D) , where the represent attitude means for the th person in each room
ONE-WAY ANOVA FOR ATTITUDE BY COLOR
Give the null hypothesis for the ANOVA F-test shown on the printout.
A) , where the s represent the proportion with the corresponding attitude
B) , where the s represent the room colors
C) , where the
D) , where the represent attitude means for the th person in each room

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
71
When a variable is identified as reducing variation in the response variable, but no additional knowledge concerning the variable is desired, it should be used as the blocking factor in the randomized block design.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
72
A certain HMO is attempting to show the benefits of managed care to an insurance company. The HMO believes that certain types of doctors are more cost-effective than others. One theory is that certification level is an important factor in measuring the cost-effectiveness of physicians. To investigate this, the HMO obtained independent random samples of 27 physicians from each of the three certification levels-Board certified (C); Uncertified, board eligible (E); and Uncertified, board ineligible (I)-and recorded the total per-member, per-month charges for each (a total of 27 physicians). In order to compare the mean charges for the three groups, the data will be subjected to an analysis of variance. Write the null hypothesis tested by the ANOVA.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
73
An advertising firm conducts 5 different campaigns, each in 3 different cities, to promote a certain product, and tracks the product sales attributable to each campaign in each city. Determine whether the study is observational or designed.
A) designed
B) observational
A) designed
B) observational

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
74
A certain HMO is attempting to show the benefits of managed health care to an insurance company. The HMO believes that certain types of doctors are more cost-effective than others. One theory is that primary specialty is an important factor in measuring the cost-effectiveness of physicians. To investigate this, the HMO obtained independent random samples of 20 HMO physicians from each of four primary specialties-General Practice (GP), Internal Medicine (IM), pediatrics (PED), and Family Physician (FP)- and recorded the total per-member, per-month charges for each. In order to compare the mean charges for the four specialty groups, the data were be subjected to a one-way analysis of variance. The results of the Tukey analysis are summarized below.
Which primary specialties have significantly lower mean charges than Internal Medicine (IM)?
A) PED and FP
B) PED
C) PED, FP, and GP
D) none
Which primary specialties have significantly lower mean charges than Internal Medicine (IM)?
A) PED and FP
B) PED
C) PED, FP, and GP
D) none

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
75
A local consumer reporter wants to compare the average costs of grocery items purchased at three different supermarkets, A, B, and C. Prices (in dollars) were recorded for a sample of 60 randomly selected grocery items at each of the three supermarkets. In order to reduce item-to-item variation,
The prices were recorded for each item on the same day at each supermarket.
Identify the blocks for this experiment.
A) the 60 grocery items
B) the prices
C) the three supermarkets
D) the day on which the data were collected
The prices were recorded for each item on the same day at each supermarket.
Identify the blocks for this experiment.
A) the 60 grocery items
B) the prices
C) the three supermarkets
D) the day on which the data were collected

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
76
The intensity of a factor is called __________.
A) a factor level
B) the treatment
C) the design
D) the experimental unit
A) a factor level
B) the treatment
C) the design
D) the experimental unit

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
77
A counselor obtains SAT averages for incoming freshmen each year for a period covering 12 years, with the objective of determining the relationship between the SAT score and the year the test was given. The averages are then subjected to analysis for the purpose of drawing a conclusion regarding a trend. Determine whether the study is observational or designed.
A) observational
B) designed
A) observational
B) designed

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
78
A multiple-comparison procedure for comparing four treatment means produced the confidence intervals shown below. Rank the means from smallest to largest. Use solid lines to connect those means which are not significantly different.
A)
B) 4213
C)
D)
A)
B) 4213
C)
D)

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
79
A certain HMO is attempting to show the benefits of managed care to an insurance company. The HMO believes that certain types of doctors are more cost-effective than others. One theory is that certification level is an important factor in measuring the cost-effectiveness of physicians. To investigate this, the HMO obtained independent random samples of 20 physicians from each of the three certification levels - Board certified (C); Uncertified, board eligible (E); and Uncertified, board ineligible (I) - and recorded the total per member per month charges for each (a total of 60 physicians). In order to compare the mean charges for the three groups, the data were subjected to an analysis of variance. The results of the ANOVA are summarized in the following table. Take = 0.01
Interpret the -value of the ANOVA F -test.
A) The means of the total per member per month charges for the three groups of physicians are equal at =.01 .
B) The model is not statistically useful (at =.01 ) for prediction purposes.
C) The variances of the total per number per month charges for the three groups of physicians differ at =.01 .
D) The means of the total per member per month charges for the three groups of physicians differ at =.01 .
Interpret the -value of the ANOVA F -test.
A) The means of the total per member per month charges for the three groups of physicians are equal at =.01 .
B) The model is not statistically useful (at =.01 ) for prediction purposes.
C) The variances of the total per number per month charges for the three groups of physicians differ at =.01 .
D) The means of the total per member per month charges for the three groups of physicians differ at =.01 .

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
80

A) The highest mean differs significantly from the other two, but there is no significant difference in the other two means.
B) There is no significant difference in any of the means.
C) The lowest mean differs significantly from the other two, but there is no significant difference in the other two means.
D) All means are significantly different.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck



