Deck 8: Inferences Based on a Single Sample: Tests of Hypothesis
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/140
Play
Full screen (f)
Deck 8: Inferences Based on a Single Sample: Tests of Hypothesis
1
The State Association of Retired Teachers has recently taken flak from some of its members regarding the poor choice of the association's name. The association's by-laws require that more than 60 percent of the association must approve a name change. Rather than convene a meeting, it is first desired to use a sample to determine if meeting is necessary. Suppose the association decided to conduct a test of hypothesis using the following null and alternative hypotheses: H0: p = 0.6 HA: p > 0.6 Define a Type I Error in the context of this problem.
A) They conclude that more than 60% of the association wants a name change when that is, in fact, true.
B) They conclude that exactly 60% of the association wants a name change when that is, in fact, true.
C) They conclude that more than 60% of the association wants a name change when, in fact, that is not true.
D) They conclude that exactly 60% of the association wants a name change when, in fact, that is not true.
A) They conclude that more than 60% of the association wants a name change when that is, in fact, true.
B) They conclude that exactly 60% of the association wants a name change when that is, in fact, true.
C) They conclude that more than 60% of the association wants a name change when, in fact, that is not true.
D) They conclude that exactly 60% of the association wants a name change when, in fact, that is not true.
C
2
How many tissues should a package of tissues contain? Researchers have determined that a person uses an average of 62 tissues during a cold. Suppose a random sample of 100 people yielded the following data on the number of tissues used during a cold:  = 50, s = 16. Identify the null and alternative hypothesis for a test to determine if the mean number of tissues used during a cold is less than 62.
= 50, s = 16. Identify the null and alternative hypothesis for a test to determine if the mean number of tissues used during a cold is less than 62. 
 = 50, s = 16. Identify the null and alternative hypothesis for a test to determine if the mean number of tissues used during a cold is less than 62.
= 50, s = 16. Identify the null and alternative hypothesis for a test to determine if the mean number of tissues used during a cold is less than 62. 
A
3
A method currently used by doctors to screen women for possible breast cancer fails to detect cancer in 17% of women who actually have the disease. A new method has been developed that researchers hope will be able to detect cancer more accurately. A random sample of 74 women known to have breast cancer were screened using the new method. Of these, the new method failed to detect cancer in ten. Specify the null and alternative hypotheses that the researchers wish to test.
To determine if the new method is more accurate in detecting cancer than the old method, we test: 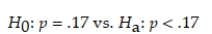
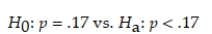
4
The owner of Get-A-Away Travel has recently surveyed a random sample of 480 customers to determine whether the mean age of the agency's customers is over 28. The appropriate hypotheses are H0: μ = 28, Ha: μ > 28. If he concludes the mean age is over 28 when it is not, he makes a __________ error. If he concludes the mean age is not over 28 when it is, he makes a __________ error.
A) Type I; Type II
B) Type II; Type II
C) Type I; Type I
D) Type II; Type I
A) Type I; Type II
B) Type II; Type II
C) Type I; Type I
D) Type II; Type I

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
5
The null hypothesis represents the status quo to the party performing the sampling experiment.

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
6
I want to test using a test of hypothesis. If I concluded that p is .7 when, in fact, the true value of p is not .7, then I have made a __________.
A) Type II error
B) Type I error
C) correct decision
D) Type I and Type II error
A) Type II error
B) Type I error
C) correct decision
D) Type I and Type II error

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
7
Suppose we wish to test . What will result if we conclude that the mean is greater than 58 when its true value is really 63?
A) a correct decision
B) a Type II error
C) a Type I error
D) none of the above
A) a correct decision
B) a Type II error
C) a Type I error
D) none of the above

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
8
An insurance company sets up a statistical test with a null hypothesis that the average time for processing a claim is 4 days, and an alternative hypothesis that the average time for processing a claim is greater than 4 days. After completing the statistical test, it is concluded that the average time exceeds 4 days. However, it is eventually learned that the mean process time is really 4 days. What type of error occurred in the statistical test?
A) Type I error
B) Type II error
C) Type III error
D) No error occurred in the statistical sense.
A) Type I error
B) Type II error
C) Type III error
D) No error occurred in the statistical sense.

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
9
A __________ is a numerical quantity computed from the data of a sample and is used in reaching a decision on whether or not to reject the null hypothesis.
A) test statistic
B) critical value
C) parameter
D) significance level
A) test statistic
B) critical value
C) parameter
D) significance level

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
10


Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
11
According to an advertisement, a strain of soybeans planted on soil prepared with a specified fertilizer treatment has a mean yield of 594 bushels per acre. Twenty farmers who belong to a cooperative plant the soybeans in soil prepared as specified. Each uses a 40-acre plot and records the mean yield per acre. The mean and variance for the sample of 20 farms are 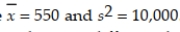 . Specify the null and alternative hypotheses used to determine if the mean yield for the soybeans is different than advertised.
. Specify the null and alternative hypotheses used to determine if the mean yield for the soybeans is different than advertised.
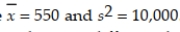 . Specify the null and alternative hypotheses used to determine if the mean yield for the soybeans is different than advertised.
. Specify the null and alternative hypotheses used to determine if the mean yield for the soybeans is different than advertised.
Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
12


Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
13
What is the probability associated with not making a Type II error? 


Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
14
A significance level for a hypothesis test is given as . Interpret this value.
A) The probability of making a Type I error is .01.
B) The smallest value of ? that you can use and still reject H0 is .01.
C) The probability of making a Type II error is .99.
D) There is a 1% chance that the sample will be biased.
A) The probability of making a Type I error is .01.
B) The smallest value of ? that you can use and still reject H0 is .01.
C) The probability of making a Type II error is .99.
D) There is a 1% chance that the sample will be biased.

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
15
A consumer product magazine recently ran a story concerning the increasing prices of digital cameras. The story stated that digital camera prices dipped a couple of years ago, but are now beginning to increase in price because of added features. According to the story, the average price of all digital cameras a couple of years ago was $215.00. A random sample of cameras was recently taken and entered into a spreadsheet. It was desired to test to determine if that average price of all digital cameras is now more than $215.00. What null and alternative hypothesis should be tested?  Answer the question True or False.
Answer the question True or False.
 Answer the question True or False.
Answer the question True or False.
Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
16
The alternative hypothesis is accepted as true unless there is overwhelming evidence that it is false.

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
17
Researchers have claimed that the average number of headaches per student during a semester of Statistics is 10. Statistics students believe the average is higher. In a sample of n = 24 students the mean is 15 headaches with a deviation of 2. Which of the following represent the null and alternative hypotheses necessary to test the students' belief? 


Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
18
If I specify β to be .36, then the value of α must be .64.

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
19
A revenue department is under orders to reduce the time small business owners spend filling out pension form ABC-5500. Previously the average time spent on the form was 6.3 hours. In order to test whether the time to fill out the form has been reduced, a sample of 53 small business owners who annually complete the form was randomly chosen, and their completion times recorded. The mean completion time for ABC-5500 form was 6.1 hours with a standard deviation of 2.6 hours. In order to test that the time to complete the form has been reduced, state the appropriate null and alternative hypotheses. 


Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
20
A local eat-in pizza restaurant wants to investigate the possibility of starting to deliver pizzas. The owner of the store has determined that home delivery will be successful only if the average time spent on a delivery does not exceed 34 minutes. The owner has randomly selected 19 customers and delivered pizzas to their homes. What hypotheses should the owner test to demonstrate that the pizza delivery will not be successful? 


Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
21
We do not accept H0 because we are concerned with making a Type II error.

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
22
For the given rejection region, sketch the sampling distribution for z and indicate the location of the rejection region.
z < -1.28
z < -1.28

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
23


Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
24


Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
25
The rejection region for a two-tailed test with α = .05 is -1.96 < z < 1.96.

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
26


Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
27
The hypotheses for 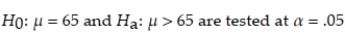 . Sketch the appropriate rejection region.
. Sketch the appropriate rejection region.
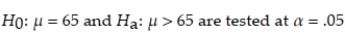 . Sketch the appropriate rejection region.
. Sketch the appropriate rejection region.
Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
28
A rejection region is established in each tail of the sampling distribution for a two-tailed test.

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
29
The hypotheses for 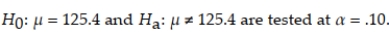 . Sketch the appropriate rejection region.
. Sketch the appropriate rejection region.
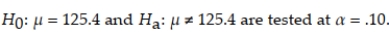 . Sketch the appropriate rejection region.
. Sketch the appropriate rejection region.
Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
30


Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
31
The State Association of Retired Teachers has recently taken flak from some of its members regarding the poor choice of the association's name. The association's by-laws require that more than 60 percent of the association must approve a name change. Rather than convene a meeting, it is first desired to use a sample to determine if meeting is necessary. Identify the null and alternative hypothesis that should be tested to determine if a name change is warranted. 


Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
32
The State Association of Retired Teachers has recently taken flak from some of its members regarding the poor choice of the association's name. The association's by-laws require that more than 60 percent of the association must approve a name change. Rather than convene a meeting, it is first desired to use a sample to determine if meeting is necessary. Suppose the association decided to conduct a test of hypothesis using the following null and alternative hypotheses: H0: p = 0.6 HA: p > 0.6 Define a Type II Error in the context of this problem.
A) They conclude that more than 60% of the association wants a name change when that is, in fact, true.
B) They conclude that exactly 60% of the association wants a name change when that is, in fact, true.
C) They conclude that more than 60% of the association wants a name change when, in fact, that is not true.
D) They conclude that exactly 60% of the association wants a name change when, in fact, that is not true.
A) They conclude that more than 60% of the association wants a name change when that is, in fact, true.
B) They conclude that exactly 60% of the association wants a name change when that is, in fact, true.
C) They conclude that more than 60% of the association wants a name change when, in fact, that is not true.
D) They conclude that exactly 60% of the association wants a name change when, in fact, that is not true.

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
33
In a test of hypothesis, the sampling distribution of the test statistic is calculated under the assumption that the alternative hypothesis is true.

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
34
Consider the following printout. HYPOTHESIS: VARIANCE
Suppose we tested Ha: ? < 2.4. Find the appropriate rejection region if we used ? = .05.
A) Reject if z < -1.645.
B) Reject if z > 1.645 or z < -1.645.
C) Reject if z > 1.96 or z < -1.96.
D) Reject if z < -1.96.
Suppose we tested Ha: ? < 2.4. Find the appropriate rejection region if we used ? = .05.
A) Reject if z < -1.645.
B) Reject if z > 1.645 or z < -1.645.
C) Reject if z > 1.96 or z < -1.96.
D) Reject if z < -1.96.

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
35


Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
36
The rejection region refers to the values of the test statistic for which we will reject the alternative hypothesis.

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
37
For the given rejection region, sketch the sampling distribution for z and indicate the location of the rejection region.
z < -1.96
z < -1.96

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
38
For the given rejection region, sketch the sampling distribution for z and indicate the location of the rejection region.
z < -2.05 or z > 2.05
z < -2.05 or z > 2.05

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
39
A Type I error occurs when we accept a false null hypothesis.

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
40
For the given rejection region, sketch the sampling distribution for z and indicate the location of the rejection region.
z < -2.33 or z > 2.33
z < -2.33 or z > 2.33

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
41


Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
42
A large university is interested in learning about the average time it takes students to drive to campus. The university sampled 238 students and asked each to provide the amount of time they spent traveling to campus. This variable, travel time, was then used conduct a test of hypothesis. The goal was to determine if the average travel time of all the university's students differed from 20 minutes. Find the large-sample rejection region for the test of interest to the college when using a level of significance of 0.05.
A) Reject H0 if z < -1.645 or z > 1.645.
B) Reject H0 if z < -1.96 or z > 1.96.
C) Reject H0 if z > 1.645.
D) Reject H0 if z < -1.96.
A) Reject H0 if z < -1.645 or z > 1.645.
B) Reject H0 if z < -1.96 or z > 1.96.
C) Reject H0 if z > 1.645.
D) Reject H0 if z < -1.96.

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
43
A supermarket sells rotisserie chicken at a fixed price per chicken rather than by the weight of the chicken. The store advertises that the average weight of their chickens is 4.6 pounds. A random sample of 30 of the store's chickens yielded the weights (in pounds) shown below.  Test whether the population mean weight of the chickens is less than 4.6 pounds. Use α = .05.
Test whether the population mean weight of the chickens is less than 4.6 pounds. Use α = .05.
 Test whether the population mean weight of the chickens is less than 4.6 pounds. Use α = .05.
Test whether the population mean weight of the chickens is less than 4.6 pounds. Use α = .05.
Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
44
The scores on a standardized test are reported by the testing agency to have a mean of 70. Based on his personal observations, a school guidance counselor believes the mean score is much higher. He collects the following scores from a sample of 50 randomly chosen students who took the test. 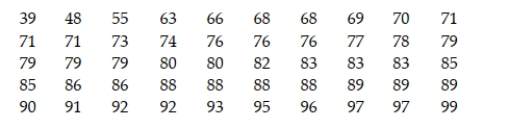 Use the data to conduct a test of hypotheses at α = .05 to determine whether there is any evidence to support the counselor's suspicions.
Use the data to conduct a test of hypotheses at α = .05 to determine whether there is any evidence to support the counselor's suspicions.
 Use the data to conduct a test of hypotheses at α = .05 to determine whether there is any evidence to support the counselor's suspicions.
Use the data to conduct a test of hypotheses at α = .05 to determine whether there is any evidence to support the counselor's suspicions.
Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
45
A consumer product magazine recently ran a story concerning the increasing prices of digital cameras. The story stated that digital camera prices dipped a couple of years ago, but now are beginning to increase in price because of added features. According to the story, the average price of all digital cameras a couple of years ago was $215.00. A random sample of n = 200 cameras was recently taken and entered into a spreadsheet. It was desired to test to determine if that average price of all digital cameras is now more than $215.00. Find the large-sample rejection region appropriate for this test if we are using α = 0.05. 


Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
46
Consider a test of H0: μ = 30 performed with the computer. SPSS reports a two-tailed p-value of 0.0164. Make the appropriate conclusion for the given situation: Ha: μ > 30, z = -2.4, α = 0.01
A) Fail to reject H0
B) Reject H0
A) Fail to reject H0
B) Reject H0

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
47


Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
48


Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
49
A revenue department is under orders to reduce the time small business owners spend filling out pension form ABC-5500. Previously the average time spent on the form was 67 hours. In order to test whether the time to fill out the form has been reduced, a sample of 81 small business owners who annually complete the form was randomly chosen and their completion times recorded. The mean completion time for the sample was 66.7 hours with a standard deviation of 15 hours. State the rejection region for the desired test at α = .10.

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
50


Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
51
Consider a test of H0: μ = 65 performed with the computer. SPSS reports a two-tailed p-value of 0.0892. Make the appropriate conclusion for the given situation: Ha: μ < 65, z = -1.7, α = 0.05
A) Reject H0
B) Fail to reject H0
A) Reject H0
B) Fail to reject H0

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
52
State University uses thousands of fluorescent light bulbs each year. The brand of bulb it currently uses has a mean life of 940 hours. A competitor claims that its bulbs, which cost the same as the brand the university currently uses, have a mean life of more than 940 hours. The university has decided to purchase the new brand if, when tested, the evidence supports the manufacturer's claim at the .01 significance level. Suppose 99 bulbs were tested with the following results: 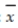 = 962 hours, s = 77 hours. Find the rejection region for the test of interest to the State University.
= 962 hours, s = 77 hours. Find the rejection region for the test of interest to the State University.
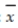 = 962 hours, s = 77 hours. Find the rejection region for the test of interest to the State University.
= 962 hours, s = 77 hours. Find the rejection region for the test of interest to the State University.
Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
53


Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
54
State University uses thousands of fluorescent light bulbs each year. The brand of bulb it currently uses has a mean life of 800 hours. A competitor claims that its bulbs, which cost the same as the brand the university currently uses, have a mean life of more than 800 hours. The university has decided to purchase the new brand if, when tested, the evidence supports the manufacturer's claim at the .05 significance level. Suppose 121 bulbs were tested with the following results: 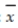 = 827.5 hours, s = 110 hours. Conduct the test using α = .05.
= 827.5 hours, s = 110 hours. Conduct the test using α = .05.
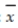 = 827.5 hours, s = 110 hours. Conduct the test using α = .05.
= 827.5 hours, s = 110 hours. Conduct the test using α = .05.
Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
55


Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
56


Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
57
A large university is interested in learning about the average time it takes students to drive to campus. The university sampled 238 students and asked each to provide the amount of time they spent traveling to campus. This variable, travel time, was then used conduct a test of hypothesis. The goal was to determine if the average travel time of all the university's students differed from 20 minutes. Suppose the sample mean and sample standard deviation were calculated to be 23.2 and 20.26 minutes, respectively. Calculate the value of the test statistic to be used in the test.
A) z = 2.437
B) z = 37.59
C) z = 0.173
D) z = 2.551
A) z = 2.437
B) z = 37.59
C) z = 0.173
D) z = 2.551

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
58
A national organization has been working with utilities throughout the nation to find sites for large wind machines that generate electricity. Wind speeds must average more than 16 miles per hour (mph) for a site to be acceptable. Recently, the organization conducted wind speed tests at a particular site. Based on a sample of n = 50 wind speed recordings (taken at random intervals), the wind speed at the site averaged x = 16.7 mph, with a standard deviation of s = 3.6 mph. To determine whether the site meets the organization's requirements, consider the test, H0: μ = 16 vs. Ha: μ > 16, where μ is the true mean wind speed at the site and α = .01. Suppose the value of the test statistic were computed to be 1.37. State the conclusion.
A) At α = .01, there is insufficient evidence to conclude the true mean wind speed at the site exceeds 16 mph.
B) At α = .01, there is sufficient evidence to conclude the true mean wind speed at the site exceeds 16 mph.
C) We are 99% confident that the site meets the organization's requirements.
D) We are 99% confident that the site does not meet the organization's requirements.
A) At α = .01, there is insufficient evidence to conclude the true mean wind speed at the site exceeds 16 mph.
B) At α = .01, there is sufficient evidence to conclude the true mean wind speed at the site exceeds 16 mph.
C) We are 99% confident that the site meets the organization's requirements.
D) We are 99% confident that the site does not meet the organization's requirements.

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
59
Consider a test of H0: μ = 70 performed with the computer. SPSS reports a two-tailed p-value of 0.2302. Make the appropriate conclusion for the given situation: Ha: μ > 70, z = 1.20, α = 0.10
A) Fail to reject H0
B) Reject H0
A) Fail to reject H0
B) Reject H0

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
60


Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
61
In a test of H0: μ = 65 against Ha: μ > 65, the sample data yielded the test statistic z = 1.38. Find and interpret the p-value for the test.

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
62
A national organization has been working with utilities throughout the nation to find sites for large wind machines that generate electricity. Wind speeds must average more than 10 miles per hour (mph) for a site to be acceptable. Recently, the organization conducted wind speed tests at a particular site. To determine whether the site meets the organization's requirements, consider the test, H0: μ = 10 vs. Ha: μ > 10, where μ is the true mean wind speed at the site and α = .01. Suppose the observed significance level (p-value) of the test is calculated to be p = 0.2991. Interpret this result.
A) Since the p-value exceeds α = .01, there is insufficient evidence to reject the null hypothesis.
B) The probability of rejecting the null hypothesis is 0.2991.
C) We are 70.09% confident that μ = 10.
D) Since the p-value greatly exceeds α = .01, there is strong evidence to reject the null hypothesis.
A) Since the p-value exceeds α = .01, there is insufficient evidence to reject the null hypothesis.
B) The probability of rejecting the null hypothesis is 0.2991.
C) We are 70.09% confident that μ = 10.
D) Since the p-value greatly exceeds α = .01, there is strong evidence to reject the null hypothesis.

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
63
A large university is interested in learning about the average time it takes students to drive to campus. The university sampled 238 students and asked each to provide the amount of time they spent traveling to campus. This variable, travel time, was then used conduct a test of hypothesis. The goal was to determine if the average travel time of all the university's students differed from 20 minutes. Suppose the large-sample test statistic was calculated to be z = 2.14. Find the p-value for this test of hypothesis.
A) p = 0.4838
B) p = 0.9838
C) p = 0.0162
D) p = 0.0324
A) p = 0.4838
B) p = 0.9838
C) p = 0.0162
D) p = 0.0324

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
64
A small private college is interested in determining the percentage of its students who live off campus and drive to class. Specifically, it was desired to determine if less than 20% of their current students live off campus and drive to class. Suppose a sample of 108 students produced a test statistic of z = -1.35. Find the p-value for the test of interest to the college.
A) p = 0.4115
B) p = 0.9115
C) p = 0.1770
D) p = 0.0885
A) p = 0.4115
B) p = 0.9115
C) p = 0.1770
D) p = 0.0885

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
65
A local eat-in pizza restaurant wants to investigate the possibility of starting to deliver pizzas. The owner of the store has determined that home delivery will be successful only if the average time spent on a delivery does not exceed 30 minutes. The owner has randomly selected 17 customers and delivered pizzas to their homes in order to test whether the mean delivery time actually exceeds 30 minutes. What assumption is necessary for this test to be valid?
A) The population of delivery times must have a normal distribution.
B) The population variance must equal the population mean.
C) The sample mean delivery time must equal the population mean delivery time.
D) None. The Central Limit Theorem makes any assumptions unnecessary.
A) The population of delivery times must have a normal distribution.
B) The population variance must equal the population mean.
C) The sample mean delivery time must equal the population mean delivery time.
D) None. The Central Limit Theorem makes any assumptions unnecessary.

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
66
In a test of H0: μ = 12 against Ha: μ > 12, a sample of n = 75 observations possessed mean 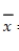 = 13.1 and standard deviation s = 4.3. Find and interpret the p-value for the test.
= 13.1 and standard deviation s = 4.3. Find and interpret the p-value for the test.
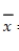 = 13.1 and standard deviation s = 4.3. Find and interpret the p-value for the test.
= 13.1 and standard deviation s = 4.3. Find and interpret the p-value for the test.
Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
67
A supermarket sells rotisserie chicken at a fixed price per chicken rather than by the weight of the chicken. The store advertises that the average weight of their chickens is 4.6 pounds. A random sample of 30 of the store's chickens yielded the weights (in pounds) shown below.  Find and interpret the p-value in a test of H0: μ = 4.6 against Ha: μ < 4.6.
Find and interpret the p-value in a test of H0: μ = 4.6 against Ha: μ < 4.6.
 Find and interpret the p-value in a test of H0: μ = 4.6 against Ha: μ < 4.6.
Find and interpret the p-value in a test of H0: μ = 4.6 against Ha: μ < 4.6.
Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
68
Data were collected from the sale of 25 properties by a local real estate agent. The following printout concentrated on the land value variable from the sampled properties. HYPOTHESIS: MEAN X = x X = land_value SAMPLE MEAN OF X = 50,098 SAMPLE VARIANCE OF X = 273,643,254 SAMPLE SIZE OF X = 25 x = 45,655 MEAN X - x = 4443 t = 1.34293 D.F. = 24 P-VALUE = 0.1918585 P-VALUE/2 = 0.0959288 SD. ERROR = 3308.43 Find the p-value for testing whether the mean land value differs from $45,655.
A) p = 0.1918585
B) p = 0.0959288
C) p = 0.808142
D) p = 0.308142
A) p = 0.1918585
B) p = 0.0959288
C) p = 0.808142
D) p = 0.308142

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
69
The smaller the p-value in a test of hypothesis, the more significant the results are.

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
70
Data were collected from the sale of 25 properties by a local real estate agent. The following printout concentrated on the land value variable from the sampled properties. HYPOTHESIS: MEAN X = x X = land_value SAMPLE MEAN OF X = 51,288 SAMPLE VARIANCE OF X = 273,643,254 SAMPLE SIZE OF X = 25 x = 46,845 MEAN X - x = 4443 t = 1.34293 D.F. = 24 P-VALUE = 0.1918585 P-VALUE/2 = 0.0959288 SD. ERROR = 3308.43 Suppose we are interested in testing whether the mean land value from this neighborhood differs from 46,845. Which hypotheses would you test? 


Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
71
A consumer product magazine recently ran a story concerning the increasing prices of digital cameras. The story stated that digital camera prices dipped a couple of years ago, but now are beginning to increase in price because of added features. According to the story, the average price of all digital cameras a couple of years ago was $215.00. A random sample of cameras was recently taken and entered into a spreadsheet. It was desired to test to determine if that average price of all digital cameras is now more than $215.00. The information was entered into a spreadsheet and the following printout was obtained: One-Sample T Test
Null Hypothesis:
Alternative Hyp:
Cases Included 22 Use the p- value given above to determine which of the following conclusions is correct.
A) At ? = 0.01, there is sufficient evidence to indicate that the mean price of all digital cameras exceeds $215.00
B) At ? = 0.05, there is insufficient evidence to indicate that the mean price of all digital cameras exceeds $215.00
C) At ? = 0.10, there is insufficient evidence to indicate that the mean price of all digital cameras exceeds $215.00
D) At ? = 0.03, there is insufficient evidence to indicate that the mean price of all digital cameras exceeds $215.00
Null Hypothesis:
Alternative Hyp:
Cases Included 22 Use the p- value given above to determine which of the following conclusions is correct.
A) At ? = 0.01, there is sufficient evidence to indicate that the mean price of all digital cameras exceeds $215.00
B) At ? = 0.05, there is insufficient evidence to indicate that the mean price of all digital cameras exceeds $215.00
C) At ? = 0.10, there is insufficient evidence to indicate that the mean price of all digital cameras exceeds $215.00
D) At ? = 0.03, there is insufficient evidence to indicate that the mean price of all digital cameras exceeds $215.00

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
72
A large university is interested in learning about the average time it takes students to drive to campus. The university sampled 238 students and asked each to provide the amount of time they spent traveling to campus. This variable, travel time, was then used to create a confidence interval and to conduct a test of hypothesis, both of which are shown in the printout below. One-Sample Z Test
Null Hypothesis:
Alternative Hyp:
Cases Included 238 What conclusion can be made from the test of hypothesis conducted in this printout? Begin each answer with, "When testing at ? = 0.01…"
A) …there is sufficient evidence to indicate that the average travel time of all students is equal to 20 minutes.
B) …there is insufficient evidence to indicate that the average travel time of all students exceeds 20 minutes.
C) …there is sufficient evidence to indicate that the average travel time of all students exceeds 20 minutes.
D) …there is insufficient evidence to indicate that the average travel time of all students is equal to 20 minutes.
Null Hypothesis:
Alternative Hyp:
Cases Included 238 What conclusion can be made from the test of hypothesis conducted in this printout? Begin each answer with, "When testing at ? = 0.01…"
A) …there is sufficient evidence to indicate that the average travel time of all students is equal to 20 minutes.
B) …there is insufficient evidence to indicate that the average travel time of all students exceeds 20 minutes.
C) …there is sufficient evidence to indicate that the average travel time of all students exceeds 20 minutes.
D) …there is insufficient evidence to indicate that the average travel time of all students is equal to 20 minutes.

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
73
In a test of H0: μ = 70 against Ha: μ ≠70, the sample data yielded the test statistic z = 2.11. Find and interpret the p-value for the test.

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
74
A local eat-in pizza restaurant wants to investigate the possibility of starting to deliver pizzas. The owner of the store has determined that home delivery will be successful only if the average time spent on a delivery does not exceed 35 minutes. The owner has randomly selected 24 customers and delivered pizzas to their homes in order to test whether the mean delivery time actually exceeds 35 minutes. Suppose the p-value for the test was found to be .0274. State the correct conclusion.
A) At α = .025, we fail to reject H0.
B) At α = .05, we fail to reject H0.
C) At α = .02, we reject H0.
D) At α = .03, we fail to reject H0.
A) At α = .025, we fail to reject H0.
B) At α = .05, we fail to reject H0.
C) At α = .02, we reject H0.
D) At α = .03, we fail to reject H0.

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
75
Based on the information in the screen below, what would you conclude in the test of H0: μ ≤ 14, Ha: μ > 14. Use α = .01. 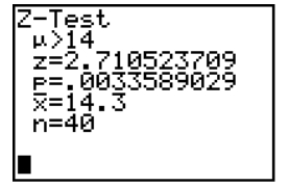


Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
76
If a hypothesis test were conducted using α = 0.05, to which of the following p-values would cause the null hypothesis to be rejected.
A) 0.040
B) 0.060
C) 0.100
D) 0.055
A) 0.040
B) 0.060
C) 0.100
D) 0.055

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
77
A bottling company produces bottles that hold 10 ounces of liquid. Periodically, the company gets complaints that their bottles are not holding enough liquid. To test this claim, the bottling company randomly samples 49 bottles and finds the average amount of liquid held by the bottles is 9.9155 ounces with a standard deviation of 0.35 ounce. Suppose the p-value of this test is 0.0455. State the proper conclusion.
A) At α = 0.05, reject the null hypothesis.
B) At α = 0.035, accept the null hypothesis.
C) At α = 0.085, fail to reject the null hypothesis.
D) At α = 0.025, reject the null hypothesis.
A) At α = 0.05, reject the null hypothesis.
B) At α = 0.035, accept the null hypothesis.
C) At α = 0.085, fail to reject the null hypothesis.
D) At α = 0.025, reject the null hypothesis.

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
78
In a test of H0: μ = 250 against Ha: μ ≠ 250, a sample of n = 100 observations possessed mean 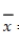 = 247.3 and standard deviation s = 11.4. Find and interpret the p-value for the test.
= 247.3 and standard deviation s = 11.4. Find and interpret the p-value for the test.
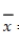 = 247.3 and standard deviation s = 11.4. Find and interpret the p-value for the test.
= 247.3 and standard deviation s = 11.4. Find and interpret the p-value for the test.
Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
79
The scores on a standardized test are reported by the testing agency to have a mean of 75. Based on his personal observations, a school guidance counselor believes the mean score is much higher. He collects the following scores from a sample of 50 randomly chosen students who took the test. 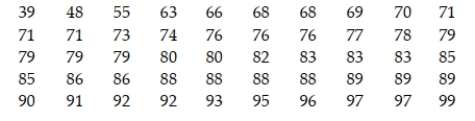 Find and interpret the p-value for the test of H0: μ = 75 against Ha: μ > 75.
Find and interpret the p-value for the test of H0: μ = 75 against Ha: μ > 75.
 Find and interpret the p-value for the test of H0: μ = 75 against Ha: μ > 75.
Find and interpret the p-value for the test of H0: μ = 75 against Ha: μ > 75.
Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck
80
Data were collected from the sale of 25 properties by a local real estate agent. The following printout concentrated on the land value variable from the sampled properties. HYPOTHESIS: MEAN X = x X = land_value SAMPLE MEAN OF X = 51,315 SAMPLE VARIANCE OF X = 273,643,254 SAMPLE SIZE OF X = 25 x = 46,872 MEAN X - x = 4443 t = 1.34293 D.F. = 24 P-VALUE = 0.1918585 P-VALUE/2 = 0.0959288 SD. ERROR = 3308.43 What is the correct conclusion when testing a greater-than alternative hypothesis at α = .01?
A) Fail to reject H0.
B) Accept H0.
C) Reject H0.
D) Fail to reject Ha.
A) Fail to reject H0.
B) Accept H0.
C) Reject H0.
D) Fail to reject Ha.

Unlock Deck
Unlock for access to all 140 flashcards in this deck.
Unlock Deck
k this deck



