Deck 4: Discrete Random Variables
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/133
Play
Full screen (f)
Deck 4: Discrete Random Variables
1
Classify the following random variable according to whether it is discrete or continuous. The number of phone calls to the attendance office of a high school on any given school day
A) discrete
B) continuous
A) discrete
B) continuous
A
2
Explain why the following is or is not a valid probability distribution for the discrete random variable x. 

This is not a valid probability distribution because the sum of the probabilities is less than 1.
3
Explain why the following is or is not a valid probability distribution for the discrete random variable x. 

This is not a valid probability distribution because the sum of the probabilities is greater than 1.
4
The school newspaper surveyed 100 commuter students and asked two questions. First, students were asked how many courses they were currently enrolled in. Second, the commuter students were asked to estimate how long it took them to drive to campus. Considering these two variables, number of courses would best be considered a _________ variable and drive time would be considered a _________ variable.
A) discrete; continuous
B) discrete; discrete
C) continuous; continuous
D) continuous; discrete
A) discrete; continuous
B) discrete; discrete
C) continuous; continuous
D) continuous; discrete

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
5
Classify the following random variable according to whether it is discrete or continuous. The number of cups of coffee sold in a cafeteria during lunch
A) discrete
B) continuous
A) discrete
B) continuous

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
6
The Fresh Oven Bakery knows that the number of pies it can sell varies from day to day. The owner believes that on 50% of the days she sells 100 pies. On another 25% of the days she sells 150 pies, and she sells 200 pies on the remaining 25% of the days. To make sure she has enough product, the owner bakes 200 pies each day at a cost of $2.50 each. Assume any pies that go unsold are thrown out at the end of the day. If she sells the pies for $3 each, find the probability distribution for her daily profit. 


Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
7
Classify the following random variable according to whether it is discrete or continuous. The number of pills in a container of vitamins
A) discrete
B) continuous
A) discrete
B) continuous

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
8
Classify the following random variable according to whether it is discrete or continuous. The blood pressures of a group of students the day before the final exam
A) continuous
B) discrete
A) continuous
B) discrete

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
9
Explain why the following is or is not a valid probability distribution for the discrete random variable x. 


Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
10
A coin is flipped 6 times. The variable x represents the number of tails obtained. List the possible values of x. Is x discrete or continuous? Explain.

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
11
Explain why the following is or is not a valid probability distribution for the discrete random variable x. 


Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
12
50 students were randomly sampled and asked questions about their exercise habits. One of the questions they were asked concerned the frequency of exercise, defined to be the number of times they exercised in a week. This variable would be characterized as which type of random variable?
A) discrete
B) continuous
A) discrete
B) continuous

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
13
Classify the following random variable according to whether it is discrete or continuous. The number of goals scored in a soccer game
A) discrete
B) continuous
A) discrete
B) continuous

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
14
A bottle contains 16 ounces of water. The variable x represents the volume, in ounces, of water remaining in the bottle after the first drink is taken. What are the natural bounds for the values of x? Is x discrete or continuous? Explain.

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
15
Consider the given discrete probability distribution. Construct a graph for p(x). 


Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
16
Classify the following random variable according to whether it is discrete or continuous. The height of a player on a basketball team
A) continuous
B) discrete
A) continuous
B) discrete

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
17
A discrete random variable x can assume five possible values: 2, 3, 5, 8, 10. Its probability distribution is shown below. Find the probability for the value of x = 5.
A) 0.7
B) 0.1
C) 0.3
D) 0.2
A) 0.7
B) 0.1
C) 0.3
D) 0.2

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
18
Management at a home improvement store randomly selected 95 customers and observed their shopping habits. They recorded the number of items each of the customers purchased as well as the total time the customers spent in the store. Identify the types of variables recorded by the managers of the home improvement store.
A) number of items - discrete; total time - continuous
B) number of items - continuous; total time - continuous
C) number of items - continuous; total time - discrete
D) number of items - discrete; total time - discrete
A) number of items - discrete; total time - continuous
B) number of items - continuous; total time - continuous
C) number of items - continuous; total time - discrete
D) number of items - discrete; total time - discrete

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
19
Classify the following random variable according to whether it is discrete or continuous. The temperature in degrees Fahrenheit on July 4th in Juneau, Alaska
A) continuous
B) discrete
A) continuous
B) discrete

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
20
Classify the following random variable according to whether it is discrete or continuous. The speed of a car on a Los Angeles freeway during rush hour traffic
A) continuous
B) discrete
A) continuous
B) discrete

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
21
A dice game involves rolling three dice and betting on one of the six numbers that are on the dice. The game costs $11 to play, and you win if the number you bet appears on any of the dice. The distribution for the outcomes of the game (including the profit) is shown below: 0 -$11 125/216 Find your expected profit from playing this game.
A) -$1.53
B) $0.50
C) $11.20
D) $5.96
A) -$1.53
B) $0.50
C) $11.20
D) $5.96

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
22
Consider the given discrete probability distribution. Find P(x = 1 or x = 2). 


Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
23
Consider the given discrete probability distribution. Find P(x ? 4).
A) .95
B) .90
C) .05
D) .10
A) .95
B) .90
C) .05
D) .10

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
24
The expected value of a discrete random variable must be one of the values in which the random variable can result.

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
25
A lab orders a shipment of 100 frogs each week. Prices for the weekly shipments of frogs follow the distribution below: Suppose the mean cost of the frogs is $12.63 per week. Interpret this value.
A) The average cost for all weekly frog purchases is $12.63.
B) Most of the weeks resulted in frog costs of $12.63.
C) The median cost for the distribution of frog costs is $12.63.
D) The frog cost that occurs more often than any other is $12.63.
A) The average cost for all weekly frog purchases is $12.63.
B) Most of the weeks resulted in frog costs of $12.63.
C) The median cost for the distribution of frog costs is $12.63.
D) The frog cost that occurs more often than any other is $12.63.

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
26
Consider the given discrete probability distribution. Find P(x < 2 or x > 3). 


Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
27
Consider the given discrete probability distribution. Find P(x > 3).
A) .5
B) .7
C) .2
D) .3
A) .5
B) .7
C) .2
D) .3

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
28
Consider the given discrete probability distribution. Construct a graph for p(x). 


Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
29
A local bakery has determined a probability distribution for the number of cheesecakes it sells in a given day. The distribution is as follows: Find the number of cheesecakes that this local bakery expects to sell in a day.
A) 11.65
B) 11.79
C) 20
D) 10
A) 11.65
B) 11.79
C) 20
D) 10

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
30
An airline has requests for standby flights at half of the usual one-way air fare. Past experience has shown that these passengers have about a 1 in 5 chance of getting on the standby flight. When they fail to get on a flight as a standby, the only other choice is to fly first class on the next flight out. Suppose that the usual one-way air fare to a certain city is $156 and the cost of flying first class is $355. Should a passenger who wishes to fly to this city opt to fly as a standby? [Hint: Find the expected cost of the trip for a person flying standby.]

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
31
Consider the given discrete probability distribution. Find the probability that x equals 5.
A) 0.09
B) 0.91
C) 0.45
D) 4.55
A) 0.09
B) 0.91
C) 0.45
D) 4.55

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
32
A lab orders a shipment of 100 frogs each week. Prices for the weekly shipments of frogs follow the distribution below: How much should the lab budget for next year's frog orders assuming this distribution does not change? (Hint: Find the expected price and assume 52 weeks per year.)
A) $617.50
B) $11.88
C) $1188.00
D) $3,211,000.00
A) $617.50
B) $11.88
C) $1188.00
D) $3,211,000.00

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
33
A discrete random variable x can assume five possible values: 2, 3, 5, 8, 10. Its probability distribution is shown below. Find the standard deviation of the distribution. 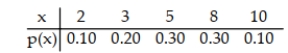
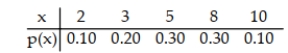

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
34
An automobile insurance company estimates the following loss probabilities for the next year on a $25,000 sports car:  Assuming the company will sell only a $500 deductible policy for this model (i.e., the owner covers the first $500 damage), how much annual premium should the company charge in order to average $620 profit per policy sold? 2 Find Mean, Variance, Standard Deviation
Assuming the company will sell only a $500 deductible policy for this model (i.e., the owner covers the first $500 damage), how much annual premium should the company charge in order to average $620 profit per policy sold? 2 Find Mean, Variance, Standard Deviation
 Assuming the company will sell only a $500 deductible policy for this model (i.e., the owner covers the first $500 damage), how much annual premium should the company charge in order to average $620 profit per policy sold? 2 Find Mean, Variance, Standard Deviation
Assuming the company will sell only a $500 deductible policy for this model (i.e., the owner covers the first $500 damage), how much annual premium should the company charge in order to average $620 profit per policy sold? 2 Find Mean, Variance, Standard Deviation
Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
35
A discrete random variable x can assume five possible values: 2, 3, 5, 8, 10. Its probability distribution is shown below. Find the mean of the distribution. 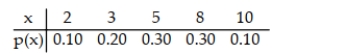
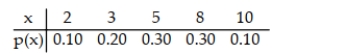

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
36
In a pizza takeout restaurant, the following probability distribution was obtained for the number of toppings ordered on a large pizza. Find the mean and standard deviation for the random variable.
A) mean: 1.14; standard deviation: 1.04
B) mean: 1.54; standard deviation: 1.30
C) mean: 1.30; standard deviation: 2.38
D) mean: 1.30; standard deviation: 1.54
A) mean: 1.14; standard deviation: 1.04
B) mean: 1.54; standard deviation: 1.30
C) mean: 1.30; standard deviation: 2.38
D) mean: 1.30; standard deviation: 1.54

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
37
The random variable x represents the number of boys in a family with three children. Assuming that births of boys and girls are equally likely, find the mean and standard deviation for the random variable x.
A) mean: 1.50; standard deviation: .87
B) mean: 2.25; standard deviation: .87
C) mean: 1.50; standard deviation: .76
D) mean: 2.25; standard deviation: .76
A) mean: 1.50; standard deviation: .87
B) mean: 2.25; standard deviation: .87
C) mean: 1.50; standard deviation: .76
D) mean: 2.25; standard deviation: .76

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
38
Calculate the mean for the discrete probability distribution shown here.
A) 6.01
B) 6
C) 24
D) 1.5025
A) 6.01
B) 6
C) 24
D) 1.5025

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
39
A discrete random variable x can assume five possible values: 2, 3, 5, 8, 10. Its probability distribution is shown below. Find the probability that the random variable x is a value greater than 5.
A) 0.40
B) 0.70
C) 0.30
D) 0.60
A) 0.40
B) 0.70
C) 0.30
D) 0.60

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
40
Mamma Temte bakes six pies each day at a cost of $2 each. On 39% of the days she sells only two pies. On 38% of the days, she sells 4 pies, and on the remaining 23% of the days, she sells all six pies. If Mama Temte sells her pies for $4 each, what is her expected profit for a day's worth of pies? [Assume that any leftover pies are given away.]
A) $2.72
B) $14.72
C) -$8.00
D) -$8.32
A) $2.72
B) $14.72
C) -$8.00
D) -$8.32

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
41
Compute
A) 1
B) 4
C) 6
D) 16
A) 1
B) 4
C) 6
D) 16

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
42
Compute 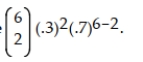
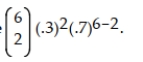

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
43
If x is a binomial random variable, compute p(x) for n = 5, x = 1, p = 0.4.
A) 0.2592
B) 0.2411
C) 0.2929
D) 0.2722
A) 0.2592
B) 0.2411
C) 0.2929
D) 0.2722

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
44
If x is a binomial random variable, compute p(x) for n = 5, x = 1, q = 0.8.
A) 0.4096
B) 0.0064
C) 0.3850
D) 0.0068
A) 0.4096
B) 0.0064
C) 0.3850
D) 0.0068

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
45
The binomial distribution can be used to model the number of rare events that occur over a given time period.

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
46
Calculate the mean for the discrete probability distribution shown here. 


Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
47
Find the mean and standard deviation of the probability distribution for the random variable x, which represents the number of cars per household in a small town. 


Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
48
Compute
A) 35
B) 210
C) 840
D) 70
A) 35
B) 210
C) 840
D) 70

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
49
For a binomial distribution, which probability is not equal to the probability of 1 success in 5 trials where the probability of success is .4?
A) the probability of 4 failures in 5 trials where the probability of success is .6
B) the probability of 1 success in 5 trials where the probability of failure is .6
C) the probability of 4 failures in 5 trials where the probability of success is .4
D) the probability of 4 failures in 5 trials where the probability of failure is .6 .
A) the probability of 4 failures in 5 trials where the probability of success is .6
B) the probability of 1 success in 5 trials where the probability of failure is .6
C) the probability of 4 failures in 5 trials where the probability of success is .4
D) the probability of 4 failures in 5 trials where the probability of failure is .6 .

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
50
For a binomial distribution, if the probability of success is .48 on the first trial, what is the probability of failure on the second trial?

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
51
A recent article in the paper claims that business ethics are at an all-time low. Reporting on a recent sample, the paper claims that 42% of all employees believe their company president possesses low ethical standards. Suppose 20 of a company's employees are randomly and independently sampled and asked if they believe their company president has low ethical standards and their years of experience at the company. Could the probability distribution for the number of years of experience be modelled by a binomial probability distribution?
A) No, a binomial distribution requires only two possible outcomes for each experimental unit sampled.
B) Yes, the sample is a random and independent sample.
C) Yes, the sample size is n = 20.
D) No, the employees would not be considered independent in the present sample.
A) No, a binomial distribution requires only two possible outcomes for each experimental unit sampled.
B) Yes, the sample is a random and independent sample.
C) Yes, the sample size is n = 20.
D) No, the employees would not be considered independent in the present sample.

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
52
Which binomial probability is represented on the screen below? 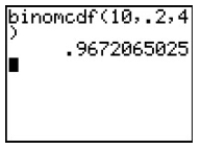




Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
53
For a binomial distribution, if the probability of success is .63 on the first trial, what is the probability of success on the second trial?

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
54
Compute
A) 126
B) 84
C) 3024
D) 15,120
A) 126
B) 84
C) 3024
D) 15,120

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
55
Consider the given discrete probability distribution. 


Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
56
A recent study suggested that 70% of all eligible voters will vote in the next presidential election. Suppose 20 eligible voters were randomly selected from the population of all eligible voters. Which of the following is necessary for this problem to be analyzed using the binomial random variable? I. There are two outcomes possible for each of the 20 voters sampled. II. The outcomes of the 20 voters must be considered independent of one another. III. The probability a voter will actually vote is 0.70, the probability they won't is 0.30. A) I only B) II only C) III only D) I, II, and III

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
57
Compute
A) 5
B) 1
C) 10
D) 20
A) 5
B) 1
C) 10
D) 20

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
58
Compute
A) 1
B) 5
C) 10
D) undefined
A) 1
B) 5
C) 10
D) undefined

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
59
A binomial random variable is defined to be the number of units sampled until x successes is observed.

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
60
Which binomial probability is represented on the screen below? 
A) The probability of 2 successes in 8 trials where the probability of success is .3.
B) The probability of 8 failures in 2 trials where the probability of failure is .3.
C) The probability of 2 successes in 8 trials where the probability of failure is .3.
D) The probability of 8 successes in 2 trials where the probability of success is .3.

A) The probability of 2 successes in 8 trials where the probability of success is .3.
B) The probability of 8 failures in 2 trials where the probability of failure is .3.
C) The probability of 2 successes in 8 trials where the probability of failure is .3.
D) The probability of 8 successes in 2 trials where the probability of success is .3.

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
61
A new drug is designed to reduce a person's blood pressure. Thirteen randomly selected hypertensive patients receive the new drug. Suppose the probability that a hypertensive patient's blood pressure drops if he or she is untreated is 0.5. Then what is the probability of observing 11 or more blood pressure drops in a random sample of 13 treated patients if the new drug is in fact ineffective in reducing blood pressure? Round to six decimal places.

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
62
If x is a binomial random variable, calculate σ2 for n = 70 and p = 0.2.
A) 11.2
B) 14
C) 3.347
D) 2.8
A) 11.2
B) 14
C) 3.347
D) 2.8

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
63
If x is a binomial random variable, calculate μ for n = 70 and p = 0.4.
A) 28
B) 35
C) 2.8
D) 16.8
A) 28
B) 35
C) 2.8
D) 16.8

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
64
A recent study suggested that 70% of all eligible voters will vote in the next presidential election. Suppose 20 eligible voters were randomly selected from the population of all eligible voters. Use a binomial probability table to find the probability that more than 12 of the eligible voters sampled will vote in the next presidential election.
A) 0.392
B) 0.228
C) 0.772
D) 0.608
E) 0.887
A) 0.392
B) 0.228
C) 0.772
D) 0.608
E) 0.887

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
65
According to a published study, 1 in every 4 men has been involved in a minor traffic accident. Suppose we have randomly and independently sampled twenty-five men and asked each whether he has been involved in a minor traffic accident. How many of the 25 men do we expect to have never been involved in a minor traffic accident? Round to the nearest whole number.
A) 19
B) 4
C) 6
D) 25
A) 19
B) 4
C) 6
D) 25

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
66
A literature professor decides to give a 15-question true-false quiz. She wants to choose the passing grade such that the probability of passing a student who guesses on every question is less than .10. What score should be set as the lowest passing grade?
A) 11
B) 9
C) 12
D) 10
A) 11
B) 9
C) 12
D) 10

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
67
We believe that 82% of the population of all Business Statistics students consider statistics to be an exciting subject. Suppose we randomly and independently selected 39 students from the population. If the true percentage is really 82%, find the probability of observing 38 or more students who consider statistics to be an exciting subject. Round to six decimal places.
A) 0.004161
B) 0.000435
C) 0.003726
D) 0.995839
A) 0.004161
B) 0.000435
C) 0.003726
D) 0.995839

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
68
A recent article in the paper claims that business ethics are at an all-time low. Reporting on a recent sample, the paper claims that 42% of all employees believe their company president possesses low ethical standards. Assume that responses were randomly and independently collected. A president of a local company that employs 1,000 people does not believe the paper's claim applies to her company. If the claim is true, how many of her company's employees believe that she possesses low ethical standards?
A) 420
B) 42
C) 580
D) 958
A) 420
B) 42
C) 580
D) 958

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
69
We believe that 90% of the population of all Business Statistics students consider statistics to be an exciting subject. Suppose we randomly and independently selected 24 students from the population and observed fewer than five in our sample who consider statistics to be an exciting subject. Make an inference about the belief that 90% of the students consider statistics to be an exciting subject.
A) The 90% number is too high. The real percentage is lower than 90%.
B) The 90% number is too low. The real percentage is higher than 90%.
C) The 90% number is exactly right.
D) It is impossible to make any inferences about the 90% number based on this information.
A) The 90% number is too high. The real percentage is lower than 90%.
B) The 90% number is too low. The real percentage is higher than 90%.
C) The 90% number is exactly right.
D) It is impossible to make any inferences about the 90% number based on this information.

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
70
It a recent study of college students indicated that 30% of all college students had at least one tattoo. A small private college decided to randomly and independently sample 15 of their students and ask if they have a tattoo. Use a binomial probability table to find the probability that exactly 5 of the students reported that they did have at least one tattoo.
A) 0.722
B) 0.515
C) 0.207
D) 0.218
A) 0.722
B) 0.515
C) 0.207
D) 0.218

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
71
If x is a binomial random variable, calculate σ for n = 100 and p = 0.3. Round to three decimal places when necessary.
A) 4.583
B) 30
C) 21
D) 5.477
A) 4.583
B) 30
C) 21
D) 5.477

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
72
An automobile manufacturer has determined that 30% of all gas tanks that were installed on its 2002 compact model are defective. If 14 of these cars are independently sampled, what is the probability that more than half need new gas tanks?

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
73
About 40% of the general population donate time and energy to community projects. Suppose 15 people have been randomly selected from a community and each asked whether he or she donates time and energy to community projects. Let x be the number who donate time and energy to community projects. Use a binomial probability table to find the probability that more than five of the 15 donate time and energy to community projects.

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
74
The probability that an individual is left-handed is 0.16. In a class of 80 students, what is the mean and standard deviation of the number of left-handed students? Round to the nearest hundredth when necessary.
A) mean: 12.8; standard deviation: 3.28
B) mean: 80; standard deviation: 3.28
C) mean: 12.8; standard deviation: 3.58
D) mean: 80; standard deviation: 3.58
A) mean: 12.8; standard deviation: 3.28
B) mean: 80; standard deviation: 3.28
C) mean: 12.8; standard deviation: 3.58
D) mean: 80; standard deviation: 3.58

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
75
A local newspaper claims that 70% of the items advertised in its classifieds section are sold within 1 week of the first appearance of the ad. To check the validity of the claim, the newspaper randomly selected n = 25 advertisements from last year's classifieds and contacted the people who placed the ads. They found that 16 of the 25 items sold within a week. Based on the newspaper's claim, is it likely to observe  who sold their item within a week? Use a binomial probability table.
who sold their item within a week? Use a binomial probability table.
 who sold their item within a week? Use a binomial probability table.
who sold their item within a week? Use a binomial probability table.
Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
76
According to a recent study, 1 in every 6 women has been a victim of domestic abuse at some point in her life. Suppose we have randomly and independently sampled twenty-five women and asked each whether she has been a victim of domestic abuse at some point in her life. Find the probability that more than 22 of the women sampled have not been the victim of domestic abuse.
A) 0.188687
B) 0.062896
C) 0.125791
D) 0.807120
A) 0.188687
B) 0.062896
C) 0.125791
D) 0.807120

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
77
A recent article in the paper claims that business ethics are at an all-time low. Reporting on a recent sample, the paper claims that 44% of all employees believe their company president possesses low ethical standards. Suppose 20 of a company's employees are randomly and independently sampled. Assuming the paper's claim is correct, find the probability that more than eight but fewer than 12 of the 20 sampled believe the company's president possesses low ethical standards. Round to six decimal places.
A) 0.437608
B) 0.285201
C) 0.669843
D) 0.809834
A) 0.437608
B) 0.285201
C) 0.669843
D) 0.809834

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
78
According to a recent study, 1 in every 9 women has been a victim of domestic abuse at some point in her life. Suppose we have randomly and independently sampled twenty-five women and asked each whether she has been a victim of domestic abuse at some point in her life. Find the probability that at least 2 of the women sampled have been the victim of domestic abuse. Round to six decimal places.
A) 0.782924
B) 0.246677
C) 0.536248
D) 0.217076
A) 0.782924
B) 0.246677
C) 0.536248
D) 0.217076

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
79
A recent study suggested that 70% of all eligible voters will vote in the next presidential election. Suppose 20 eligible voters were randomly selected from the population of all eligible voters. Use a binomial probability table to find the probability that more than 10 but fewer than 16 of the 20 eligible voters sampled will vote in the next presidential election.
A) 0.780
B) 0.714
C) 0.845
D) 0.649
A) 0.780
B) 0.714
C) 0.845
D) 0.649

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck
80
A recent survey found that 63% of all adults over 50 wear glasses for driving. In a random sample of 20 adults over 50, what is the mean and standard deviation of the number who wear glasses? Round to the nearest hundredth when necessary.
A) mean: 12.6; standard deviation: 2.16
B) mean: 12.6; standard deviation: 3.55
C) mean: 7.4; standard deviation: 2.16
D) mean: 7.4; standard deviation: 3.55
A) mean: 12.6; standard deviation: 2.16
B) mean: 12.6; standard deviation: 3.55
C) mean: 7.4; standard deviation: 2.16
D) mean: 7.4; standard deviation: 3.55

Unlock Deck
Unlock for access to all 133 flashcards in this deck.
Unlock Deck
k this deck



