Deck 5: Discrete Random Variables
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/163
Play
Full screen (f)
Deck 5: Discrete Random Variables
1
Provide an appropriate response.
A person is trying to decide which of two possible mutual funds to invest his money in. Let
the random variable X represent the annual return for mutual fund A and let the random
variable Y represent the annual return for fund B. It is known that the mean, µ, of X is
10.3% and the standard deviation, Ϭ, of X is 4.2%. It is also known that the mean, µ, of Y is
11.3% and the standard deviation, Ϭ, of Y is 7.2%. Which fund do you think the person
would prefer if he is a short-term investor? Which fund do you think he would prefer if he
is a long-term investor? Explain your thinking.
A person is trying to decide which of two possible mutual funds to invest his money in. Let
the random variable X represent the annual return for mutual fund A and let the random
variable Y represent the annual return for fund B. It is known that the mean, µ, of X is
10.3% and the standard deviation, Ϭ, of X is 4.2%. It is also known that the mean, µ, of Y is
11.3% and the standard deviation, Ϭ, of Y is 7.2%. Which fund do you think the person
would prefer if he is a short-term investor? Which fund do you think he would prefer if he
is a long-term investor? Explain your thinking.
A short-term investor would probably prefer
fund A as it is less volatile (the standard deviation of the returns is smaller). A
long-term investor would probably prefer fund B as it has a higher mean return. For
a long-term investor the volatility of fund B poses less of a risk.
fund A as it is less volatile (the standard deviation of the returns is smaller). A
long-term investor would probably prefer fund B as it has a higher mean return. For
a long-term investor the volatility of fund B poses less of a risk.
2
Provide an appropriate response.
Identify each of the variables in the Binomial Probability Formula.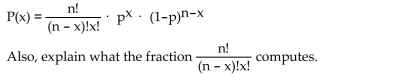
Identify each of the variables in the Binomial Probability Formula.
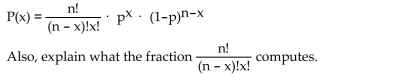
n is the fixed number of trials, x is the number of successes, p is the probability of
success in one of the n trials, and (1 - p)is the probability of failure in one of the n
trials. The fraction determines the number of different orders of x successes out of n
trials.
success in one of the n trials, and (1 - p)is the probability of failure in one of the n
trials. The fraction determines the number of different orders of x successes out of n
trials.
3
Solve the problem.
The number of lightning strikes in a year at the top of a particular mountain has a Poisson
distribution
with parameter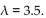 . Construct a histogram of the probabilities when the number of
. Construct a histogram of the probabilities when the number of
strikes is from 1-5.
The number of lightning strikes in a year at the top of a particular mountain has a Poisson
distribution
with parameter
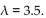 . Construct a histogram of the probabilities when the number of
. Construct a histogram of the probabilities when the number ofstrikes is from 1-5.
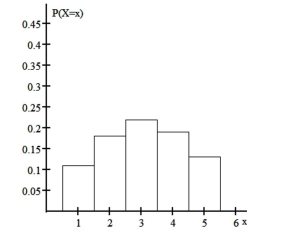
4
Provide an appropriate response.
A coin is biased so that the probability it will come up tails is 0.43. The coin is tossed three
times. Considering a success to be tails, formulate the process of observing the outcome of
the three tosses as a sequence of three Bernoulli trials. Complete the table below by
showing each possible outcome together with its probability. Display the probabilities to
three decimal places. List the outcomes in which exactly two of the three tosses are tails.
Without using the binomial probability formula, find the probability that exactly two of the
three tosses are tails.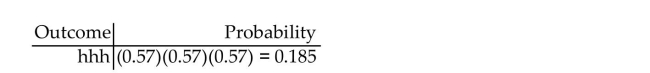
A coin is biased so that the probability it will come up tails is 0.43. The coin is tossed three
times. Considering a success to be tails, formulate the process of observing the outcome of
the three tosses as a sequence of three Bernoulli trials. Complete the table below by
showing each possible outcome together with its probability. Display the probabilities to
three decimal places. List the outcomes in which exactly two of the three tosses are tails.
Without using the binomial probability formula, find the probability that exactly two of the
three tosses are tails.

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
5
Provide an appropriate response.
Five cards are drawn at random, with replacement, from an ordinary deck of 52 cards.
Considering success to be drawing a heart, formulate the process of observing the suits of
the five cards as a sequence of five Bernoulli trials.
Five cards are drawn at random, with replacement, from an ordinary deck of 52 cards.
Considering success to be drawing a heart, formulate the process of observing the suits of
the five cards as a sequence of five Bernoulli trials.

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
6
Provide an appropriate response.
A game is said to be "fair" if the expected value for winnings is 0, that is, in the long run,
the player can expect to win 0. Consider the following game. The game costs $1 to play and
the payoffs are $5 for red, $3 for blue, $2 for yellow, and nothing for white. The following
probabilities apply. What are your expected winnings? Does the game favor the player or
the owner?
A game is said to be "fair" if the expected value for winnings is 0, that is, in the long run,
the player can expect to win 0. Consider the following game. The game costs $1 to play and
the payoffs are $5 for red, $3 for blue, $2 for yellow, and nothing for white. The following
probabilities apply. What are your expected winnings? Does the game favor the player or
the owner?


Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
7
Provide an appropriate response.
Explain how you would construct a probability histogram of a discrete random variable
given its probability distribution.
Explain how you would construct a probability histogram of a discrete random variable
given its probability distribution.

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
8
Provide an appropriate response.
Suppose that the random variable X has a binomial distribution and that the success
probability, p, is greater than 0.5. Is the probability distribution of X right skewed, left
skewed, or symmetric? Explain your thinking.
Suppose that the random variable X has a binomial distribution and that the success
probability, p, is greater than 0.5. Is the probability distribution of X right skewed, left
skewed, or symmetric? Explain your thinking.

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
9
Provide an appropriate response.
Suppose a mathematician computed the expected value of winnings for a person playing
each of seven different games in a casino. What would you expect to be true for all
expected values for these seven games?
Suppose a mathematician computed the expected value of winnings for a person playing
each of seven different games in a casino. What would you expect to be true for all
expected values for these seven games?

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
10
Provide an appropriate response.
A group of potential jurors consists of 15 women and 18 men. Suppose that 12 people are
picked at random from this group, without replacement. Let X represent the number of
women among those selected. Since the sample size exceeds 5% of the population size, X
does not have an approximate binomial distribution. Explain in your own words why X
does not have a binomial distribution. Which of the requirements for a binomial
distribution does it not satisfy?
A group of potential jurors consists of 15 women and 18 men. Suppose that 12 people are
picked at random from this group, without replacement. Let X represent the number of
women among those selected. Since the sample size exceeds 5% of the population size, X
does not have an approximate binomial distribution. Explain in your own words why X
does not have a binomial distribution. Which of the requirements for a binomial
distribution does it not satisfy?

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
11
Provide an appropriate response.
40% of the adult residents of a certain city own their own home. Four residents are
selected at random from the city and asked whether or not they own their own home.
Considering a success to be "owns their own home", formulate the process of observing
whether each of the four residents owns their own home as a sequence of four Bernoulli
trials. Complete the table below by showing each possible outcome together with its
probability. Display the probabilities to three decimal places. List the outcomes in which
exactly two of the four residents own their own home. Without using the binomial
probability formula, find the probability that exactly two of the four residents own their
own home.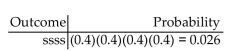
40% of the adult residents of a certain city own their own home. Four residents are
selected at random from the city and asked whether or not they own their own home.
Considering a success to be "owns their own home", formulate the process of observing
whether each of the four residents owns their own home as a sequence of four Bernoulli
trials. Complete the table below by showing each possible outcome together with its
probability. Display the probabilities to three decimal places. List the outcomes in which
exactly two of the four residents own their own home. Without using the binomial
probability formula, find the probability that exactly two of the four residents own their
own home.
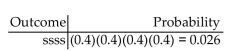

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
12
Provide an appropriate response.
Give an example of a discrete random variable whose possible values form a countable
infinite set of numbers.
Give an example of a discrete random variable whose possible values form a countable
infinite set of numbers.

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
13
Provide an appropriate response.
6.2% of VCRs of a certain type are defective. Let the random variable X represent the
number of defective VCRs among 200 randomly selected VCRs of this type. Suppose you
wish to find the probability that X is equal to 8. Does the random variable X have a
binomial or a Poisson distribution? How can you tell? If X has a binomial distribution,
would it be reasonable to use the Poisson approximation? If not, why not?
6.2% of VCRs of a certain type are defective. Let the random variable X represent the
number of defective VCRs among 200 randomly selected VCRs of this type. Suppose you
wish to find the probability that X is equal to 8. Does the random variable X have a
binomial or a Poisson distribution? How can you tell? If X has a binomial distribution,
would it be reasonable to use the Poisson approximation? If not, why not?

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
14
Provide an appropriate response.
The random variable X represents the number of thunderstorms occurring in a month in
one city. Suppose that X has a Poisson distribution with parameter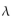 = 3.2. Determine and
= 3.2. Determine and
interpret the mean of the random variable X.
The random variable X represents the number of thunderstorms occurring in a month in
one city. Suppose that X has a Poisson distribution with parameter
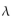 = 3.2. Determine and
= 3.2. Determine andinterpret the mean of the random variable X.

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
15
Provide an appropriate response.



Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
16
Provide an appropriate response.
Explain in your own words the meaning of the term "probability distribution".
Explain in your own words the meaning of the term "probability distribution".

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
17
Provide an appropriate response.
Let the random variable X represent the winnings at one play of a particular game. The
expected value of X is known to be -$0.32. Suppose a player plays the game five times and
calculates his average winnings. Will the average definitely be equal to -$0.32? Now
suppose the player plays the game 100 times and calculates his average winnings. Will the
average definitely be equal to -$0.32? Which average is likely to be closer to -$0.32?
Explain your answer with reference to the law of large numbers.
Let the random variable X represent the winnings at one play of a particular game. The
expected value of X is known to be -$0.32. Suppose a player plays the game five times and
calculates his average winnings. Will the average definitely be equal to -$0.32? Now
suppose the player plays the game 100 times and calculates his average winnings. Will the
average definitely be equal to -$0.32? Which average is likely to be closer to -$0.32?
Explain your answer with reference to the law of large numbers.

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
18
Provide an appropriate response.
For a particular game at a casino, let the random variable X represent the winnings (payoff
minus bet)for one play of the game. The expected value of the random variable X is
-$0.87. How would you interpret this statement?
For a particular game at a casino, let the random variable X represent the winnings (payoff
minus bet)for one play of the game. The expected value of the random variable X is
-$0.87. How would you interpret this statement?

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
19
Solve the problem.
16% of the employees of a certain company cycle to work. Three employees are selected at
random from the company and asked whether or not they cycle to work. Considering a
success to be "cycles to work", formulate the process of observing whether each of the three
employees cycles to work as a sequence of three Bernoulli trials. Complete the table below
by showing each possible outcome together with its probability. Display the probabilities
to three decimal places. List the outcomes in which exactly one of the three employees
cycles to work. Without using the binomial probability formula, find the probability that
exactly one of the three employees cycles to work.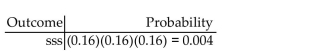
16% of the employees of a certain company cycle to work. Three employees are selected at
random from the company and asked whether or not they cycle to work. Considering a
success to be "cycles to work", formulate the process of observing whether each of the three
employees cycles to work as a sequence of three Bernoulli trials. Complete the table below
by showing each possible outcome together with its probability. Display the probabilities
to three decimal places. List the outcomes in which exactly one of the three employees
cycles to work. Without using the binomial probability formula, find the probability that
exactly one of the three employees cycles to work.
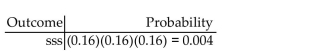

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
20
Provide an appropriate response.
Which of the following describes the possible values of a Poisson random variable, X?
A)All counting numbers (1, 2, 3, 4, ...)
B)All counting numbers up to twice the mean of X (1, 2, 3, 4, ..., 2ʎ)
C)All integers
D)All nonnegative integers
Which of the following describes the possible values of a Poisson random variable, X?
A)All counting numbers (1, 2, 3, 4, ...)
B)All counting numbers up to twice the mean of X (1, 2, 3, 4, ..., 2ʎ)
C)All integers
D)All nonnegative integers

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
21
Find the indicated binomial probability. Round to five decimal places when necessary.
In a certain college, 20% of the physics majors belong to ethnic minorities. If 10 students are selected at random from the physics majors, what is the probability that exactly 2 belong to an
Ethnic minority?
A)1.8
B)0.30199
C)0.00671
D)0.00007
In a certain college, 20% of the physics majors belong to ethnic minorities. If 10 students are selected at random from the physics majors, what is the probability that exactly 2 belong to an
Ethnic minority?
A)1.8
B)0.30199
C)0.00671
D)0.00007

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
22
Solve the problem.
A naturalist leads whale watch trips every morning in March. The number of whales seen X, has a Poisson distribution with parameter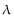 = 3.3. Construct a probability table for the random variable
= 3.3. Construct a probability table for the random variable
X. Compute the probabilities for 0 - 5 sightings.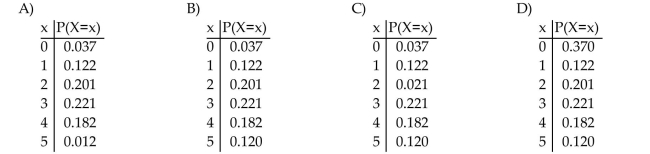
A naturalist leads whale watch trips every morning in March. The number of whales seen X, has a Poisson distribution with parameter
 = 3.3. Construct a probability table for the random variable
= 3.3. Construct a probability table for the random variableX. Compute the probabilities for 0 - 5 sightings.


Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
23
Find the standard deviation of the Poisson random variable. Round to three decimal places.
Suppose X has a Poisson distribution with parameter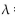 = 10.620. Find the standard deviation of X.
= 10.620. Find the standard deviation of X.
A)10.620
B)5.310
C)3.259
D)112.784
Suppose X has a Poisson distribution with parameter
 = 10.620. Find the standard deviation of X.
= 10.620. Find the standard deviation of X.A)10.620
B)5.310
C)3.259
D)112.784

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
24
Determine the required probability by using the Poisson approximation to the binomial distribution. Round to threedecimal places.
The probability that a car will have a flat tire while driving through a certain tunnel is 0.00005. Use the Poisson approximation to the binomial distribution to find the probability that among 8000 cars
Passing through this tunnel, at most two will have a flat tire.
A)0.062
B)0.054
C)0.938
D)0.992
The probability that a car will have a flat tire while driving through a certain tunnel is 0.00005. Use the Poisson approximation to the binomial distribution to find the probability that among 8000 cars
Passing through this tunnel, at most two will have a flat tire.
A)0.062
B)0.054
C)0.938
D)0.992

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
25
Provide an appropriate response.
List the four requirements for a binomial distribution. Describe an experiment which is
binomial and discuss how the experiment fits each of the four requirements.
List the four requirements for a binomial distribution. Describe an experiment which is
binomial and discuss how the experiment fits each of the four requirements.

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
26
Find the indicated binomial probability. Round to five decimal places when necessary.
A multiple choice test has 30 questions, and each has four possible answers, of which one is correct. If a student guesses on every question, find the probability of getting exactly 12 correct.
A)0.00004
B)0.02906
C)5.1554
D)13,922,008.7
A multiple choice test has 30 questions, and each has four possible answers, of which one is correct. If a student guesses on every question, find the probability of getting exactly 12 correct.
A)0.00004
B)0.02906
C)5.1554
D)13,922,008.7

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
27
Find the indicated probability. Round to four decimal places.
Find the probability of at least 2 girls in 6 births. Assume that male and female births are equally likely and that the births are independent events.
A)0.6563
B)0.2344
C)0.8906
D)0.1094
Find the probability of at least 2 girls in 6 births. Assume that male and female births are equally likely and that the births are independent events.
A)0.6563
B)0.2344
C)0.8906
D)0.1094

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
28
Use the Poisson Distribution to find the indicated probability. Round to three decimal places when necessary.



Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
29
Provide an appropriate response.
What is the probability that 6 rolls of a fair die will show four exactly 2 times?
A)0.0134
B)0.0067
C)0.41667
D)0.20094
What is the probability that 6 rolls of a fair die will show four exactly 2 times?
A)0.0134
B)0.0067
C)0.41667
D)0.20094

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
30
Provide an appropriate response.
Describe the Poisson distribution and give some example of a random variable with a
Poisson distribution.
Describe the Poisson distribution and give some example of a random variable with a
Poisson distribution.

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
31
Provide an appropriate response.
A coin is biased. Danny wishes to determine the probability of obtaining heads when
flipping this coin. He flips the coin 10 times and obtains 8 heads. He concludes that the
probability of obtaining heads when flipping this coin is 0.8. Is his thinking reasonable?
Why or why not?
A coin is biased. Danny wishes to determine the probability of obtaining heads when
flipping this coin. He flips the coin 10 times and obtains 8 heads. He concludes that the
probability of obtaining heads when flipping this coin is 0.8. Is his thinking reasonable?
Why or why not?

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
32
Find the indicated probability. Round to four decimal places.
A car insurance company has determined that 9% of all drivers were involved in a car accident last year. Among the 10 drivers living on one particular street, 3 were involved in a car accident last
Year. If 10 drivers are randomly selected, what is the probability of getting 3 or more who were
Involved in a car accident last year?
A)0.9548
B)0.0452
C)0.4435
D)0.0541
A car insurance company has determined that 9% of all drivers were involved in a car accident last year. Among the 10 drivers living on one particular street, 3 were involved in a car accident last
Year. If 10 drivers are randomly selected, what is the probability of getting 3 or more who were
Involved in a car accident last year?
A)0.9548
B)0.0452
C)0.4435
D)0.0541

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
33
Find the indicated binomial probability. Round to five decimal places when necessary.
A cat has a litter of 7 kittens. Find the probability that exactly 5 of the little furballs are female. Assume that male and female births are equally likely.
A)0.16406
B)0.32813
C)0.00781
D)0.65625
A cat has a litter of 7 kittens. Find the probability that exactly 5 of the little furballs are female. Assume that male and female births are equally likely.
A)0.16406
B)0.32813
C)0.00781
D)0.65625

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
34
Determine the required probability by using the Poisson approximation to the binomial distribution. Round to threedecimal places.
The probability that a car will have a flat tire while driving through a certain tunnel is 0.00004. Use the Poisson approximation to the binomial distribution to find the probability that among 11,000
Cars passing through this tunnel, at least one will have a flat tire.
A)0.513
B)0.356
C)0.644
D)0.283
The probability that a car will have a flat tire while driving through a certain tunnel is 0.00004. Use the Poisson approximation to the binomial distribution to find the probability that among 11,000
Cars passing through this tunnel, at least one will have a flat tire.
A)0.513
B)0.356
C)0.644
D)0.283

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
35
The probability distribution of a random variable is given along with its mean and standard deviation. Draw aprobability histogram for the random variable; locate the mean and show one, two, and three standard deviationintervals.
The random variable X is the number of tails when four coins are flipped. Its probability distribution is as follows.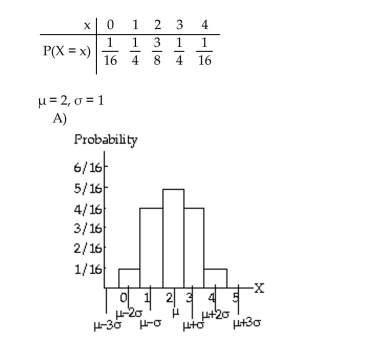
The random variable X is the number of tails when four coins are flipped. Its probability distribution is as follows.



Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
36
Find the mean of the binomial random variable. Round to two decimal places when necessary.
On a multiple choice test with 6 questions, each question has four possible answers, one of which is correct. For students who guess at all answers, find the mean for the random variable X, the
Number of correct answers.
A)4.5
B)3
C)1.5
D)2
On a multiple choice test with 6 questions, each question has four possible answers, one of which is correct. For students who guess at all answers, find the mean for the random variable X, the
Number of correct answers.
A)4.5
B)3
C)1.5
D)2

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
37
Find the standard deviation of the binomial random variable.
According to a college survey, 22% of all students work full time. Find the standard deviation for the random variable X, the number of students who work full time in samples of size 16.
A)2.75
B)3.52
C)1.66
D)1.88
According to a college survey, 22% of all students work full time. Find the standard deviation for the random variable X, the number of students who work full time in samples of size 16.
A)2.75
B)3.52
C)1.66
D)1.88

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
38
Provide an appropriate response.
The random variable X represents the number of siblings of a student selected randomly from a particular college. Use random variable notation to express the following statement in shorthand.
The random variable X represents the number of siblings of a student selected randomly from a particular college. Use random variable notation to express the following statement in shorthand.


Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
39
Provide an appropriate response.
A die is rolled repeatedly until a six appears. The random variable X represents the total number of rolls preceding the six. What are the possible values of the random variable X?
A)0, 1, 2, 3, 4, .....
B)0, 1, 2, 3, 4, 5, 6
C)1, 2, 3, 4, .....
D)1, 2, 3, 4, 5, 6
A die is rolled repeatedly until a six appears. The random variable X represents the total number of rolls preceding the six. What are the possible values of the random variable X?
A)0, 1, 2, 3, 4, .....
B)0, 1, 2, 3, 4, 5, 6
C)1, 2, 3, 4, .....
D)1, 2, 3, 4, 5, 6

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
40
Construct a probability histogram for the binomial random variable, X.
Two balls are drawn at random, with replacement, from a bag containing 4 red balls and 2 blue balls. X is the number of blue balls drawn.
Two balls are drawn at random, with replacement, from a bag containing 4 red balls and 2 blue balls. X is the number of blue balls drawn.


Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
41
Find the mean of the binomial random variable. Round to two decimal places when necessary.
In a certain town, 90 percent of voters are in favor of a given ballot measure and 10 percent are opposed. For groups of 180 voters, find the mean for the random variable X, the number who
Oppose the measure.
A)10
B)90
C)18
D)162
In a certain town, 90 percent of voters are in favor of a given ballot measure and 10 percent are opposed. For groups of 180 voters, find the mean for the random variable X, the number who
Oppose the measure.
A)10
B)90
C)18
D)162

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
42
Use the Poisson Distribution to find the indicated probability. Round to three decimal places when necessary.
In one town, the number of burglaries in a week has a Poisson distribution with parameter = 4.7 Find the probability that in a randomly selected week the number of burglaries is at least three.
= 4.7 Find the probability that in a randomly selected week the number of burglaries is at least three.
A)0.152
B)0.157
C)0.848
D)0.690
In one town, the number of burglaries in a week has a Poisson distribution with parameter
 = 4.7 Find the probability that in a randomly selected week the number of burglaries is at least three.
= 4.7 Find the probability that in a randomly selected week the number of burglaries is at least three.A)0.152
B)0.157
C)0.848
D)0.690

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
43
Find the standard deviation of the binomial random variable.
A die is rolled 17 times and the number of twos that come up is tallied. If this experiment is repeated many times, find the standard deviation for the random variable X, the number of twos.
A)1.543
B)2.06
C)1.537
D)1.491
A die is rolled 17 times and the number of twos that come up is tallied. If this experiment is repeated many times, find the standard deviation for the random variable X, the number of twos.
A)1.543
B)2.06
C)1.537
D)1.491

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
44
Use random-variable notation to represent the event.
The following table displays a frequency distribution for the number of siblings for students in one middle school. For a randomly selected student in the school, let X denote the number of siblings of
The student.
The following table displays a frequency distribution for the number of siblings for students in one middle school. For a randomly selected student in the school, let X denote the number of siblings of
The student.


Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
45
Provide an appropriate response.
Let the random variable X represent the winnings at one play of a particular game. The expected
value of X is known to be -$0.32. True or false, this means that in the long run, the average amount
lost by the player per play of the game will be 32 cents?
Let the random variable X represent the winnings at one play of a particular game. The expected
value of X is known to be -$0.32. True or false, this means that in the long run, the average amount
lost by the player per play of the game will be 32 cents?

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
46
Obtain the probability distribution of the random variable.
When two balanced dice are rolled, 36 equally likely outcomes are possible as shown below.
When two balanced dice are rolled, 36 equally likely outcomes are possible as shown below.


Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
47
Determine the possible values of the random variable.
Suppose that two balanced dice, a red die and a green die, are rolled. Let Y denote the value of G - R where G represents the number on the green die and R represents the number on the red die.
What are the possible values of the random variable Y?
Suppose that two balanced dice, a red die and a green die, are rolled. Let Y denote the value of G - R where G represents the number on the green die and R represents the number on the red die.
What are the possible values of the random variable Y?


Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
48
Find the mean of the binomial random variable. Round to two decimal places when necessary.
The probability that a person has immunity to a particular disease is 0.3. Find the mean for the random variable X, the number who have immunity in samples of size 24.
A)12
B)0.3
C)16.8
D)7.2
The probability that a person has immunity to a particular disease is 0.3. Find the mean for the random variable X, the number who have immunity in samples of size 24.
A)12
B)0.3
C)16.8
D)7.2

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
49
Use the Poisson Distribution to find the indicated probability. Round to three decimal places when necessary.



Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
50
Find the standard deviation of the binomial random variable.
A company manufactures batteries in batches of 26 and there is a 3% rate of defects. Find the standard deviation for the random variable X, the number of defects per batch.
A)0.883
B)0.853
C)0.87
D)0.867
A company manufactures batteries in batches of 26 and there is a 3% rate of defects. Find the standard deviation for the random variable X, the number of defects per batch.
A)0.883
B)0.853
C)0.87
D)0.867

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
51
Evaluate the expression.
10!
A)3,628,790
B)3,628,800
C)3,628,810
D)362,880
10!
A)3,628,790
B)3,628,800
C)3,628,810
D)362,880

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
52
Find the indicated probability. Round to four decimal places.
A company purchases shipments of machine components and uses this acceptance sampling plan: Randomly select and test 21 components and accept the whole batch if there are fewer than 3
Defectives. If a particular shipment of thousands of components actually has a 3% rate of defects,
What is the probability that this whole shipment will be accepted?
A)0.0208
B)0.9760
C)0.1060
D)0.4485
A company purchases shipments of machine components and uses this acceptance sampling plan: Randomly select and test 21 components and accept the whole batch if there are fewer than 3
Defectives. If a particular shipment of thousands of components actually has a 3% rate of defects,
What is the probability that this whole shipment will be accepted?
A)0.0208
B)0.9760
C)0.1060
D)0.4485

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
53
The probability distribution of a random variable is given along with its mean and standard deviation. Draw aprobability histogram for the random variable; locate the mean and show one, two, and three standard deviationintervals.
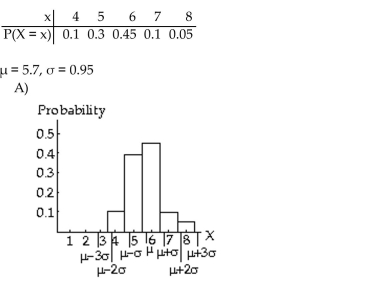
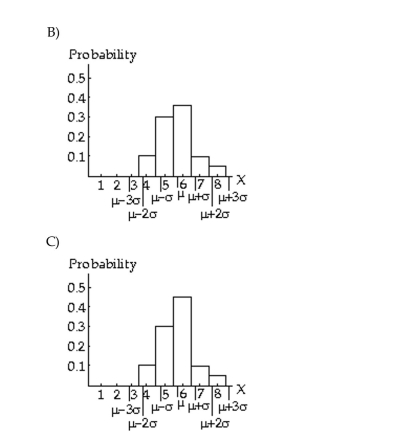



Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
54
Find the specified probability distribution of the binomial random variable.
In one city, the probability that a person will pass his or her driving test on the first attempt is 0.69. Four people are selected at random from among those taking their driving test for the first time.
Determine the probability distribution of X, the number among the four who pass the test.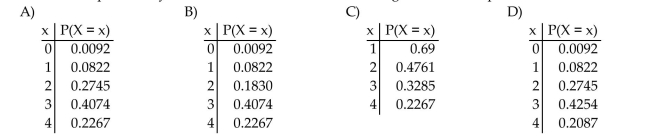
In one city, the probability that a person will pass his or her driving test on the first attempt is 0.69. Four people are selected at random from among those taking their driving test for the first time.
Determine the probability distribution of X, the number among the four who pass the test.


Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
55
Find the indicated binomial probability. Round to five decimal places when necessary.
A company manufactures calculators in batches of 64 and there is a 4% rate of defects. Find the probability of getting exactly 4 defects in a batch.
A)1.62656
B)54,866.1882
C)3.84
D)0.14046
A company manufactures calculators in batches of 64 and there is a 4% rate of defects. Find the probability of getting exactly 4 defects in a batch.
A)1.62656
B)54,866.1882
C)3.84
D)0.14046

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
56
Find the specified probability.
A statistics professor has office hours from 9:00 am to 10:00 am each day. The number of students waiting to see the professor is a random variable, X, with the distribution shown in the table.
A statistics professor has office hours from 9:00 am to 10:00 am each day. The number of students waiting to see the professor is a random variable, X, with the distribution shown in the table.


Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
57
Find the mean of the binomial random variable. Round to two decimal places when necessary.
According to a college survey, 22% of all students work full time. Find the mean for the random variable X, the number of students who work full time in samples of size 16.
A)4
B)2.75
C)3.52
D)0.22
According to a college survey, 22% of all students work full time. Find the mean for the random variable X, the number of students who work full time in samples of size 16.
A)4
B)2.75
C)3.52
D)0.22

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
58
Use random-variable notation to represent the event.
For a randomly selected student in a particular high school, let Y denote the number of living grandparents of the student. Use random-variable notation to represent the event that the student
Obtained has exactly three living grandparents.
For a randomly selected student in a particular high school, let Y denote the number of living grandparents of the student. Use random-variable notation to represent the event that the student
Obtained has exactly three living grandparents.


Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
59
Find the specified probability distribution of the binomial random variable.
A multiple choice test consists of four questions. Each question has five possible answers of which only one is correct. A student guesses on every question. Find the probability distribution of X, the
Number of questions she answers correctly.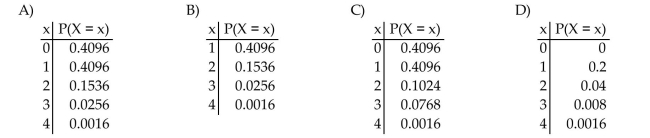
A multiple choice test consists of four questions. Each question has five possible answers of which only one is correct. A student guesses on every question. Find the probability distribution of X, the
Number of questions she answers correctly.
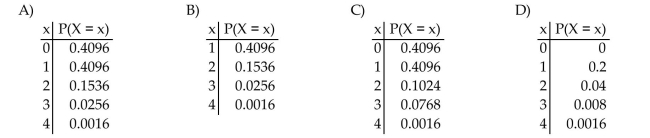

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
60
Use random-variable notation to represent the event.
Suppose that two balanced dice are rolled. Let Y denote the sum of the two numbers. Use random-variable notation to represent the event that the sum of the two numbers is at least 11.
Suppose that two balanced dice are rolled. Let Y denote the sum of the two numbers. Use random-variable notation to represent the event that the sum of the two numbers is at least 11.


Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
61
Find the indicated probability. Round to four decimal places.
In a study, 35% of adults questioned reported that their health was excellent. A researcher wishes to study the health of people living close to a nuclear power plant. Among 10 adults randomly
Selected from this area, only 3 reported that their health was excellent. Find the probability that
When 10 adults are randomly selected, 3 or fewer are in excellent health.
A)0.5138
B)0.2522
C)0.3743
D)0.2616
In a study, 35% of adults questioned reported that their health was excellent. A researcher wishes to study the health of people living close to a nuclear power plant. Among 10 adults randomly
Selected from this area, only 3 reported that their health was excellent. Find the probability that
When 10 adults are randomly selected, 3 or fewer are in excellent health.
A)0.5138
B)0.2522
C)0.3743
D)0.2616

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
62
Use random-variable notation to represent the event.
Suppose that two balanced dice are rolled. Let Y denote the sum of the two numbers. Use random-variable notation to represent the event that the sum of the two numbers is at least 3 but
Less than 5.
Suppose that two balanced dice are rolled. Let Y denote the sum of the two numbers. Use random-variable notation to represent the event that the sum of the two numbers is at least 3 but
Less than 5.


Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
63
Find the specified probability.
The number of loaves of rye bread left on the shelf of a local bakery at closing (denoted by the random variable X)varies from day to day. Past records show that the probability distribution of X
Is as shown in the following table. Find the probability that there will be at least three loaves left
Over at the end of any given day.
The number of loaves of rye bread left on the shelf of a local bakery at closing (denoted by the random variable X)varies from day to day. Past records show that the probability distribution of X
Is as shown in the following table. Find the probability that there will be at least three loaves left
Over at the end of any given day.


Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
64
Find the mean of the random variable.
The random variable X is the number of siblings of a student selected at random from a particular secondary school. Its probability distribution is given in the table. Round the answer to three
Decimal places when necessary.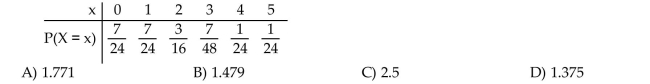
The random variable X is the number of siblings of a student selected at random from a particular secondary school. Its probability distribution is given in the table. Round the answer to three
Decimal places when necessary.
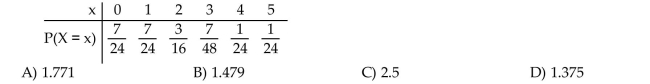

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
65
Find the mean of the random variable.
The random variable X is the number of golf balls ordered by customers at a pro shop. Its probability distribution is given in the table. Round the answer to two decimal places when
Necessary.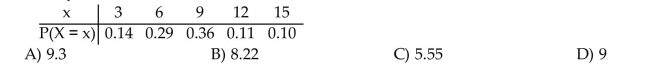
The random variable X is the number of golf balls ordered by customers at a pro shop. Its probability distribution is given in the table. Round the answer to two decimal places when
Necessary.
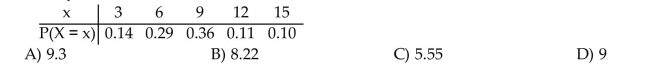

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
66
Find the mean of the random variable.
The random variable X is the number of houses sold by a realtor in a single month at the Sendsom's Real Estate office. Its probability distribution is given in the table. Round the answer to two decimal
Places when necessary.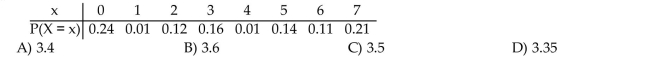
The random variable X is the number of houses sold by a realtor in a single month at the Sendsom's Real Estate office. Its probability distribution is given in the table. Round the answer to two decimal
Places when necessary.
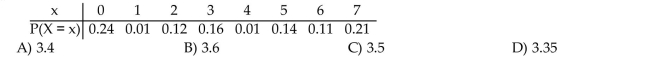

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
67
Use random-variable notation to represent the event.
Suppose that two balanced dice are rolled. Let X denote the absolute value of the difference of the two numbers. Use random-variable notation to represent the event that the absolute value of the
Difference of the two numbers is 2.
Suppose that two balanced dice are rolled. Let X denote the absolute value of the difference of the two numbers. Use random-variable notation to represent the event that the absolute value of the
Difference of the two numbers is 2.


Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
68
Obtain the probability distribution of the random variable.
-When two balanced dice are rolled, 36 equally likely outcomes are possible as shown below.
Let denote the product of the two numbers. Find the probability distribution of . Leave your probabilities in fraction form.
A)
B)
C)
D)
-When two balanced dice are rolled, 36 equally likely outcomes are possible as shown below.
Let denote the product of the two numbers. Find the probability distribution of . Leave your probabilities in fraction form.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
69
Find the mean of the Poisson random variable.
Suppose X has a Poisson distribution with parameter ʎ = 0.17. Find the mean of X.
A)0.17
B)0.085
C)0.412
D)0.03
Suppose X has a Poisson distribution with parameter ʎ = 0.17. Find the mean of X.
A)0.17
B)0.085
C)0.412
D)0.03

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
70
Calculate the specified probability



Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
71
Find the mean of the Poisson random variable.



Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
72
Evaluate the expression.



Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
73
Use the Poisson Distribution to find the indicated probability. Round to three decimal places when necessary.
The number of lightning strikes in a year at the top of a particular mountain has a Poisson distribution with parameter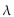 = 3.8. Find the probability that in a randomly selected year, the
= 3.8. Find the probability that in a randomly selected year, the
Number of lightning strikes is 5.
A)0.251
B)0.192
C)0.148
D)0.004
The number of lightning strikes in a year at the top of a particular mountain has a Poisson distribution with parameter
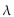 = 3.8. Find the probability that in a randomly selected year, the
= 3.8. Find the probability that in a randomly selected year, theNumber of lightning strikes is 5.
A)0.251
B)0.192
C)0.148
D)0.004

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
74
Find the indicated probability. Round to four decimal places.
An airline estimates that 93% of people booked on their flights actually show up. If the airline books 73 people on a flight for which the maximum number is 71, what is the probability that the
Number of people who show up will exceed the capacity of the plane?
A)0.0275
B)0.0325
C)0.1070
D)0.0050
An airline estimates that 93% of people booked on their flights actually show up. If the airline books 73 people on a flight for which the maximum number is 71, what is the probability that the
Number of people who show up will exceed the capacity of the plane?
A)0.0275
B)0.0325
C)0.1070
D)0.0050

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
75
Find the specified probability.



Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
76
Use random-variable notation to represent the event.
For a randomly selected student in a particular high school, let Y denote the number of living grandparents of the student. Use random-variable notation to represent the event that the student
Obtained has at least two living grandparents.
For a randomly selected student in a particular high school, let Y denote the number of living grandparents of the student. Use random-variable notation to represent the event that the student
Obtained has at least two living grandparents.


Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
77
Find the indicated probability. Round to four decimal places.
In a certain college, 33% of the physics majors belong to ethnic minorities. If 10 students are selected at random from the physics majors, what is the probability that no more than 6 belong to
An ethnic minority?
A)0.0547
B)0.9130
C)0.9846
D)0.9815
In a certain college, 33% of the physics majors belong to ethnic minorities. If 10 students are selected at random from the physics majors, what is the probability that no more than 6 belong to
An ethnic minority?
A)0.0547
B)0.9130
C)0.9846
D)0.9815

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
78
Use the Poisson Distribution to find the indicated probability. Round to three decimal places when necessary.
A computer salesman averages 1.9 sales per week. Use the Poisson distribution to find the probability that in a randomly selected week the number of computers sold is 3.
A)0.188
B)0.214
C)0.171
D)0.325
A computer salesman averages 1.9 sales per week. Use the Poisson distribution to find the probability that in a randomly selected week the number of computers sold is 3.
A)0.188
B)0.214
C)0.171
D)0.325

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
79
Find the standard deviation of the binomial random variable.
The probability of winning a certain lottery is 1/70,366. For people who play 929 times, find the standard deviation for the random variable X, the number of wins.
A)3.5021
B)0.1259
C)0.0132
D)0.1149
The probability of winning a certain lottery is 1/70,366. For people who play 929 times, find the standard deviation for the random variable X, the number of wins.
A)3.5021
B)0.1259
C)0.0132
D)0.1149

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
80
Find the mean of the binomial random variable. Round to two decimal places when necessary.
A company manufactures batteries in batches of 20 and there is a 3% rate of defects. Find the mean for the random variable X, the number of defects per batch.
A)0.6
B)0.58
C)0.62
D)19.4
A company manufactures batteries in batches of 20 and there is a 3% rate of defects. Find the mean for the random variable X, the number of defects per batch.
A)0.6
B)0.58
C)0.62
D)19.4

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck



