Deck 10: Correlation and Regression
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/129
Play
Full screen (f)
Deck 10: Correlation and Regression
1
Given the linear correlation coefficient r and the sample size n, determine the critical values of r and use your finding to state whether or not the given r represents a significant linear correlation. Use a significance level of 0.05.
-
A) Critical values: , significant linear correlation
B) Critical values: , no significant linear correlation
C) Critical values: , no significant linear correlation
D) Critical values: , significant linear correlation
-
A) Critical values: , significant linear correlation
B) Critical values: , no significant linear correlation
C) Critical values: , no significant linear correlation
D) Critical values: , significant linear correlation
Critical values: , no significant linear correlation
2
Given the linear correlation coefficient r and the sample size n, determine the critical values of r and use your finding to state whether or not the given r represents a significant linear correlation. Use a significance level of 0.05.
-
A) Critical values: , no significant linear correlation
B) Critical values: , significant linear correlation
C) Critical values: , significant linear correlation
D) Critical values: , no significant linear correlation
-
A) Critical values: , no significant linear correlation
B) Critical values: , significant linear correlation
C) Critical values: , significant linear correlation
D) Critical values: , no significant linear correlation
Critical values: , significant linear correlation
3
Provide an appropriate response.
-Explain why having a significant linear correlation does not imply causality. Give an example to support your answer.
-Explain why having a significant linear correlation does not imply causality. Give an example to support your answer.
Having a significant linear correlation does not imply causality because the relationships may coincide but not cause change in one another. Examples will vary.
4
Provide an appropriate response.
Suppose data are collected concerning the weight of a person in pounds and the number of calories burned in 30 minutes of walking on a treadmill at 3.5 mph. How would the value of the correlation coefficient, r, change if all of the weights were converted to kilograms?
Suppose data are collected concerning the weight of a person in pounds and the number of calories burned in 30 minutes of walking on a treadmill at 3.5 mph. How would the value of the correlation coefficient, r, change if all of the weights were converted to kilograms?

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
5
Construct a scatter diagram for the given data
-
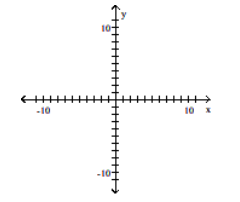
A)
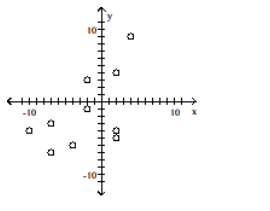
B)
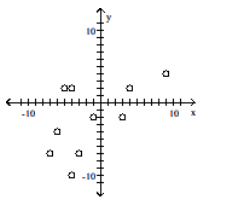
C)
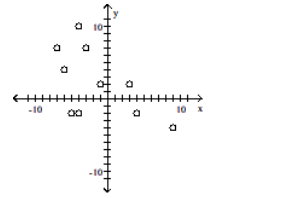
D)
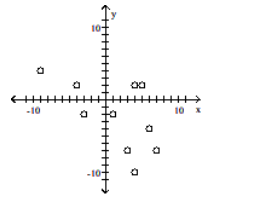
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
6
Given the linear correlation coefficient r and the sample size n, determine the critical values of r and use your finding to state whether or not the given r represents a significant linear correlation. Use a significance level of 0.05.
-
A) Critical values: , significant linear correlation
B) Critical values: , no significant linear correlation
C) Critical values: , no significant linear correlation
D) Critical values: , no significant linear correlation
-
A) Critical values: , significant linear correlation
B) Critical values: , no significant linear correlation
C) Critical values: , no significant linear correlation
D) Critical values: , no significant linear correlation

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
7
Provide an appropriate response.
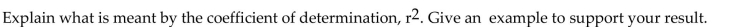
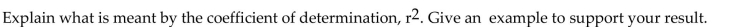

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
8
Provide an appropriate response.
-Discuss the guidelines under which the linear regression equation should be used for prediction. Refer to the correlation coefficient, the type of data used to create the linear regression, and the predicting value.
-Discuss the guidelines under which the linear regression equation should be used for prediction. Refer to the correlation coefficient, the type of data used to create the linear regression, and the predicting value.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
9
Provide an appropriate response.
-Create a scatterplot that shows a perfect positive correlation between x and y. How would the scatterplot change if the correlation showed a)a strong positive correlation, b)a positive correlation, and c)no correlation?
-Create a scatterplot that shows a perfect positive correlation between x and y. How would the scatterplot change if the correlation showed a)a strong positive correlation, b)a positive correlation, and c)no correlation?

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
10
Provide an appropriate response.
-Describe what scatterplots are, and discuss the importance of creating scatterplots.
-Describe what scatterplots are, and discuss the importance of creating scatterplots.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
11
Provide an appropriate response.
-Suppose that statisticians determine that there is a significant positive correlation between the grade earned in the class College Reading Skills and the grade earned in Statistics. Does achieving a high grade in reading cause an individual to earn a high grade in Statistics? Explain your answer with reference to the term lurking variable.
-Suppose that statisticians determine that there is a significant positive correlation between the grade earned in the class College Reading Skills and the grade earned in Statistics. Does achieving a high grade in reading cause an individual to earn a high grade in Statistics? Explain your answer with reference to the term lurking variable.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
12
Provide an appropriate response.
-Define the term independent, or predictor, variable and the term dependent, or response, variable. Give examples for each.
-Define the term independent, or predictor, variable and the term dependent, or response, variable. Give examples for each.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
13
Given the linear correlation coefficient r and the sample size n, determine the critical values of r and use your finding to state whether or not the given r represents a significant linear correlation. Use a significance level of 0.05.
-
A) Critical values: , no significant linear correlation
B) Critical values: , no significant linear correlation
C) Critical values: , significant linear correlation
D) Critical values: , no significant linear correlation
-
A) Critical values: , no significant linear correlation
B) Critical values: , no significant linear correlation
C) Critical values: , significant linear correlation
D) Critical values: , no significant linear correlation

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
14
Given the linear correlation coefficient r and the sample size n, determine the critical values of r and use your finding to state whether or not the given r represents a significant linear correlation. Use a significance level of 0.05.
-
A) Critical values: , no significant linear correlation
B) Critical values: , significant linear correlation
C) Critical values: , no significant linear correlation
D) Critical values: , significant linear correlation
-
A) Critical values: , no significant linear correlation
B) Critical values: , significant linear correlation
C) Critical values: , no significant linear correlation
D) Critical values: , significant linear correlation

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
15
Provide an appropriate response.
What is the importance of correlation in terms of the linear regression equation?
What is the importance of correlation in terms of the linear regression equation?

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
16
Provide an appropriate response.
-Suppose there is significant correlation between two variables. Describe two cases under which it might be inappropriate to use the linear regression equation for prediction. Give examples to support these cases.
-Suppose there is significant correlation between two variables. Describe two cases under which it might be inappropriate to use the linear regression equation for prediction. Give examples to support these cases.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
17
Provide an appropriate response.
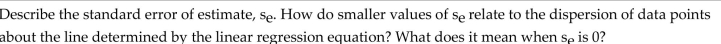

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
18
Construct a scatter diagram for the given data
-
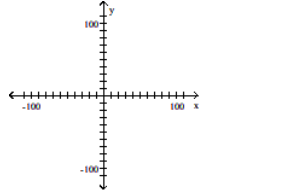
A)
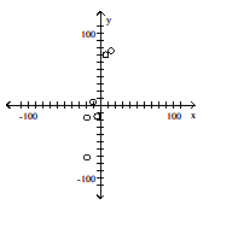
B)
C)
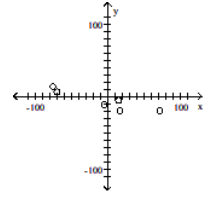
D)
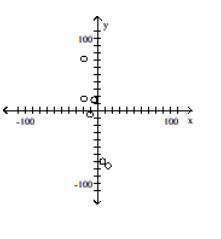
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
19
Provide an appropriate response.
-When testing to determine if correlation is significant, we use the hypotheses . Suppose the conclusion is to reject the null hypothesis. What does that tell us about the linear regression equation?
-When testing to determine if correlation is significant, we use the hypotheses . Suppose the conclusion is to reject the null hypothesis. What does that tell us about the linear regression equation?

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
20
Provide an appropriate response.
Describe what correlation is, and explain the purpose of correlation.
Describe what correlation is, and explain the purpose of correlation.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
21
Find the best predicted value of y corresponding to the given value of x.
-Four pairs of data yield and the regression equation . Also, . What is the best predicted value of for ?
A)
B)
C)
D)
-Four pairs of data yield and the regression equation . Also, . What is the best predicted value of for ?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
22
Find the value of the linear correlation coefficient r
-The paired data below consist of the costs of advertising (in thousands of dollars)and the number of products sold (in thousands):
A)
B)
C)
D)
-The paired data below consist of the costs of advertising (in thousands of dollars)and the number of products sold (in thousands):
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
23
Find the value of the linear correlation coefficient r
-Two separate tests are designed to measure a student's ability to solve problems. Several students are randomly selected to take both tests and the results are shown below.
A)0.548
B)0.109
C)0.714
D)0.867
-Two separate tests are designed to measure a student's ability to solve problems. Several students are randomly selected to take both tests and the results are shown below.
A)0.548
B)0.109
C)0.714
D)0.867

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
24
Find the value of the linear correlation coefficient r
-The paired data below consist of the test scores of 6 randomly selected students and the number of hours they studied for the test.
A)
B)
C)
D)
-The paired data below consist of the test scores of 6 randomly selected students and the number of hours they studied for the test.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
25
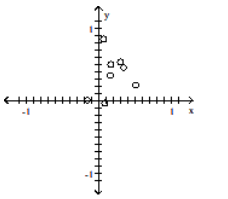
Construct a scatter diagram for the given data
-
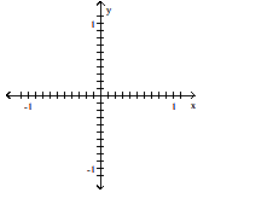
A)
B)
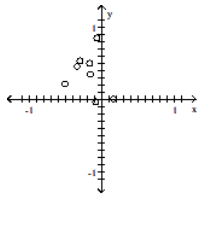
C)
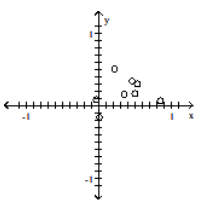
D)
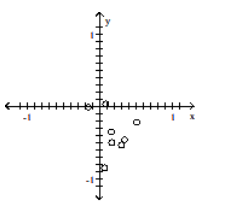
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
26
Describe the error in the stated conclusion.
-Given: There is no significant linear correlation between scores on a math test and scores on a verbal test. Conclusion: There is no relationship between scores on the math test and scores on the verbal test.
-Given: There is no significant linear correlation between scores on a math test and scores on a verbal test. Conclusion: There is no relationship between scores on the math test and scores on the verbal test.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
27
Find the best predicted value of y corresponding to the given value of x.
-Six pairs of data yield and the regression equation . Also, . What is the best predicted value of for ?
A)
B)
C)
D) 27
-Six pairs of data yield and the regression equation . Also, . What is the best predicted value of for ?
A)
B)
C)
D) 27

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
28
Find the value of the linear correlation coefficient r
-Managers rate employees according to job performance and attitude. The results for several randomly selected employees are given below.
A)0.610
B)0.863
C)0.729
D)0.916
-Managers rate employees according to job performance and attitude. The results for several randomly selected employees are given below.
A)0.610
B)0.863
C)0.729
D)0.916

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
29
Find the value of the linear correlation coefficient r
-Two different tests are designed to measure employee productivity and dexterity. Several employees are randomly selected and tested with these results.
A)
B)
C)
D)
-Two different tests are designed to measure employee productivity and dexterity. Several employees are randomly selected and tested with these results.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
30
Find the value of the linear correlation coefficient r
-
A) 0
B)
C)
D)
-
A) 0
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
31
Describe the error in the stated conclusion.
-Given: There is a significant linear correlation between the number of homicides in a town and the number of movie theaters in a town. Conclusion: Building more movie theaters will cause the homicide rate to rise.
-Given: There is a significant linear correlation between the number of homicides in a town and the number of movie theaters in a town. Conclusion: Building more movie theaters will cause the homicide rate to rise.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
32
Find the value of the linear correlation coefficient r
-A study was conducted to compare the average time spent in the lab each week versus course grade for computer students. The results are recorded in the table below.
A)
B)
C)
D)
-A study was conducted to compare the average time spent in the lab each week versus course grade for computer students. The results are recorded in the table below.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
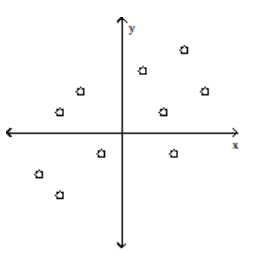
33
Determine which plot shows the strongest linear correlation
A)
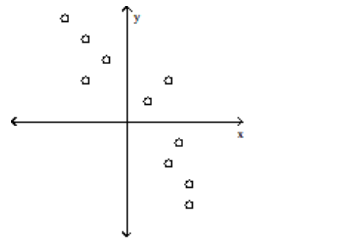
B)
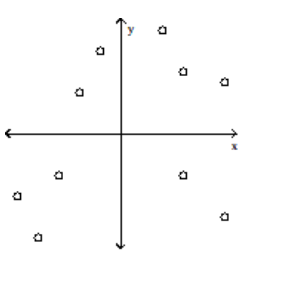
C)
A)

B)

C)


Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
34
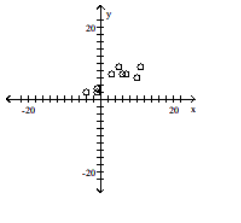
Construct a scatter diagram for the given data
-
A)
B)
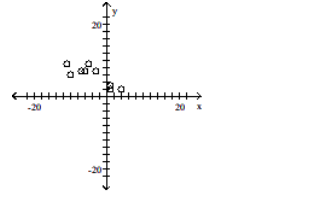
C)
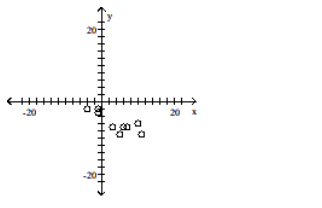
D)
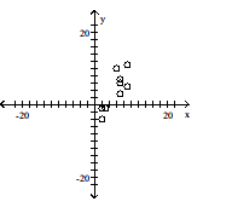
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
35
Find the value of the linear correlation coefficient r
-The paired data below consist of the temperatures on randomly chosen days and the amount a certain kind of plant grew (in millimeters):
A)
B)
C) 0
D)
-The paired data below consist of the temperatures on randomly chosen days and the amount a certain kind of plant grew (in millimeters):
A)
B)
C) 0
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
36
Determine which plot shows the strongest linear correlation
A)
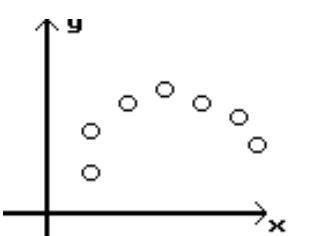
B)
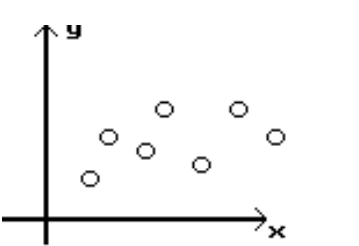
C)
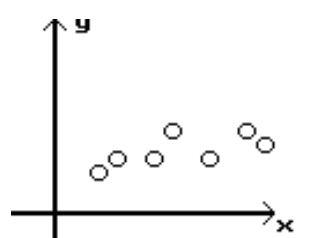
A)

B)

C)


Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
37
Describe the error in the stated conclusion.
-Given: The linear correlation coefficient between scores on a math test and scores on a test of athletic ability is negative and close to zero. Conclusion: People who score high on the math test tend to score lower on the test of athletic ability.
-Given: The linear correlation coefficient between scores on a math test and scores on a test of athletic ability is negative and close to zero. Conclusion: People who score high on the math test tend to score lower on the test of athletic ability.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
38
Find the value of the linear correlation coefficient r
-
A) 0.754
B) -0.081
C) -0.775
D) 0
-
A) 0.754
B) -0.081
C) -0.775
D) 0

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
39
Describe the error in the stated conclusion.
-Given: Each school in a state reports the average SAT score of its students. There is a significant linear correlation between the average SAT score of a school and the average annual income in the district in which the school is located. Conclusion: There is a significant linear correlation between individual SAT scores and family income.
-Given: Each school in a state reports the average SAT score of its students. There is a significant linear correlation between the average SAT score of a school and the average annual income in the district in which the school is located. Conclusion: There is a significant linear correlation between individual SAT scores and family income.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
40
Find the best predicted value of y corresponding to the given value of x.
-Eight pairs of data yield and the regression equation . Also, . What is the best oredicted value of for ?
A)
B)
C)
D)
-Eight pairs of data yield and the regression equation . Also, . What is the best oredicted value of for ?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
41
Find the best predicted value of y corresponding to the given value of x.
-Nine pairs of data yield and the regression equation . Also, . What is the best predicted value of for ?
A)
B)
C)
D)
-Nine pairs of data yield and the regression equation . Also, . What is the best predicted value of for ?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
42
Use the given data to find the equation of the regression line. Round the final values to three significant digits, if necessary.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
43
Use the given data to find the equation of the regression line. Round the final values to three significant digits, if necessary.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
44
Use the given data to find the equation of the regression line. Round the final values to three significant digits, if necessary.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
45
Use the given data to find the equation of the regression line. Round the final values to three significant digits, if necessary.
-Ten students in a graduate program were randomly selected. Their grade point averages (GPAs)when they entered the program were between 3.5 and 4.0. The following data were obtained regarding their GPAs on entering the program versus their current GPAs.
A)
B)
C)
D)
-Ten students in a graduate program were randomly selected. Their grade point averages (GPAs)when they entered the program were between 3.5 and 4.0. The following data were obtained regarding their GPAs on entering the program versus their current GPAs.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
46
Is the data point, P
-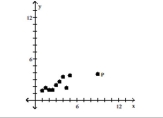
A)Outlier
B)Neither
C)Both
D)Influential point
-

A)Outlier
B)Neither
C)Both
D)Influential point

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
47
Use the given data to find the equation of the regression line. Round the final values to three significant digits, if necessary.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
48
Use the given data to find the equation of the regression line. Round the final values to three significant digits, if necessary.
-Managers rate employees according to job performance and attitude. The results for several randomly selected employees are given below.
A)
B)
C)
D)
-Managers rate employees according to job performance and attitude. The results for several randomly selected employees are given below.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
49
Is the data point, P
-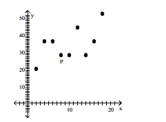
A)Influential point
B)Neither
C)Both
D)Outlier
-

A)Influential point
B)Neither
C)Both
D)Outlier

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
50
Use the given data to find the equation of the regression line. Round the final values to three significant digits, if necessary.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
51
Find the best predicted value of y corresponding to the given value of x.
-The regression equation relating attitude rating and job performance rating for the employees of a company is . Ten pairs of data were used to obtain the equation. The same data yield and . What is the best predicted job performance rating for a person whose attitude rating is 73 ?
A)
B)
C)
D)
-The regression equation relating attitude rating and job performance rating for the employees of a company is . Ten pairs of data were used to obtain the equation. The same data yield and . What is the best predicted job performance rating for a person whose attitude rating is 73 ?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
52
Use the given data to find the equation of the regression line. Round the final values to three significant digits, if necessary.
-Two different tests are designed to measure employee productivity and dexterity. Several employees are randomly selected and tested with these results.
A)
B)
C)
D)
-Two different tests are designed to measure employee productivity and dexterity. Several employees are randomly selected and tested with these results.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
53
Is the data point, P
-The regression equation for a set of paired data is . The correlation coefficient for the data is . A hew data point, , is added to the set.
A)Neither
B)Outlier
C)Both
D)Influential point
-The regression equation for a set of paired data is . The correlation coefficient for the data is . A hew data point, , is added to the set.
A)Neither
B)Outlier
C)Both
D)Influential point

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
54
Find the best predicted value of y corresponding to the given value of x.
-Ten pairs of data yield and the regression equation . Also, . What is the best predicted value of for ?
A)
B)
C)
D)
-Ten pairs of data yield and the regression equation . Also, . What is the best predicted value of for ?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
55
Is the data point, P
-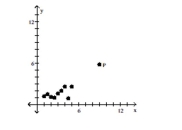
A)Neither
B)Outlier
C)Both
D)Influential point
-

A)Neither
B)Outlier
C)Both
D)Influential point

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
56
Find the best predicted value of y corresponding to the given value of x.
-The regression equation relating dexterity scores and productivity scores ( for the employees of a company . Ten pairs of data were used to obtain the equation. The same data yield and . What is the best predicted productivity score for a person whose dexterity score is 33 ?
A)
B)
C)
D)
-The regression equation relating dexterity scores and productivity scores ( for the employees of a company . Ten pairs of data were used to obtain the equation. The same data yield and . What is the best predicted productivity score for a person whose dexterity score is 33 ?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
57
Find the value of the linear correlation coefficient r.
-Based on the data from six students, the regression equation relating number of hours of preparation (x)and test score is . The same data yield and . What is the best predicted test score for a student who spent 2 hours preparing for the test?
A)69.4
B)78.1
C)75.2
D)59.7
-Based on the data from six students, the regression equation relating number of hours of preparation (x)and test score is . The same data yield and . What is the best predicted test score for a student who spent 2 hours preparing for the test?
A)69.4
B)78.1
C)75.2
D)59.7

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
58
Find the best predicted value of y corresponding to the given value of x.
-Six pairs of data yield and the regression equation . Also, . What is the best predicted value of for ?
A)
B)
C)
D)
-Six pairs of data yield and the regression equation . Also, . What is the best predicted value of for ?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
59
Use the given data to find the equation of the regression line. Round the final values to three significant digits, if necessary.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
60
Use the given data to find the equation of the regression line. Round the final values to three significant digits, if necessary.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
61
A collection of paired data consists of the number of years that students have studied Spanish and their scores on a Spanish language proficiency test. A computer program was used to obtain the least squares linear regression line and the computer output is shown below. Along with the paired sample data, the program was also given an x value of 2 (years of study)to be used for predicting test score. The regression equation is
Predicted values
What percentage of the total variation in test scores can be explained by the linear relationship between years of study and test scores?
A)82.7%
B)17.0%
C)91.1%
D)83.0%
Predicted values
What percentage of the total variation in test scores can be explained by the linear relationship between years of study and test scores?
A)82.7%
B)17.0%
C)91.1%
D)83.0%

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
62
A collection of paired data consists of the number of years that students have studied Spanish and their scores on a Spanish language proficiency test. A computer program was used to obtain the least squares linear regression line and the computer output is shown below. Along with the paired sample data, the program was also given an x value of 2 (years of study)to be used for predicting test score. The regression equation is
Predicted values
For a person who studies for 2 years, obtain the prediction interval and write a statement interpreting the in
A) ; We can be confident that the mean test score of all individuals who study 2 years will lie in the interval
B) ; We can be confident that the test score of an individual who studies 2 years will lie in the interval
C) ; We can be confident that the mean test score of all individuals who study 2 years will lie in the interval
D) ; We can be confident that the test score of an individual who studies 2 years will lie in the interval
Predicted values
For a person who studies for 2 years, obtain the prediction interval and write a statement interpreting the in
A) ; We can be confident that the mean test score of all individuals who study 2 years will lie in the interval
B) ; We can be confident that the test score of an individual who studies 2 years will lie in the interval
C) ; We can be confident that the mean test score of all individuals who study 2 years will lie in the interval
D) ; We can be confident that the test score of an individual who studies 2 years will lie in the interval

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
63
The equation of the regression line for the paired data below is . Find the unexplained variation.
A)78.75
B)10.00
C)14.25
D)88.75
A)78.75
B)10.00
C)14.25
D)88.75

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
64
A regression equation is obtained for a collection of paired data. It is found that the total variation is 114, the explained variation is 91.7, and the unexplained variation is 22.3. Find the coefficient of determination.
A)0.804
B)1.243
C)0.243
D)0.196
A)0.804
B)1.243
C)0.243
D)0.196

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
65
The equation of the regression line for the paired data below is . Find the explained variation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
66
Is the data point, P
-The regression equation for a set of paired data is . The values of run from 100 to 400 . A new data point, , is added to the set.
A)Both
B)Influential point
C)Neither
D)Outlier
-The regression equation for a set of paired data is . The values of run from 100 to 400 . A new data point, , is added to the set.
A)Both
B)Influential point
C)Neither
D)Outlier

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
67
The test scores of 6 randomly picked students and the numbers of hours they prepared are as follows:
The equation of the regression line is . Find the coefficient of determination.
A)
B)
C)
D)
The equation of the regression line is . Find the coefficient of determination.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
68
A collection of paired data consists of the number of years that students have studied Spanish and their scores on a Spanish language proficiency test. A computer program was used to obtain the least squares linear regression line and the computer output is shown below. Along with the paired sample data, the program was also given an x value of 2 (years of study)to be used for predicting test score. The regression equation is
Predicted values
Use the information in the display to find the value of the linear correlation coefficient r. Determine whether the significant linear correlation between years of study and test scores. Use a significance level of . There are 16 data.
A) ; There is significant linear correlation.
B) ; There is no significant linear correlation.
C) ; There is no significant linear correlation
D) ; There is significant linear correlation.
Predicted values
Use the information in the display to find the value of the linear correlation coefficient r. Determine whether the significant linear correlation between years of study and test scores. Use a significance level of . There are 16 data.
A) ; There is significant linear correlation.
B) ; There is no significant linear correlation.
C) ; There is no significant linear correlation
D) ; There is significant linear correlation.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
69
The equation of the regression line for the paired data below is . Find the explained variation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
70
The paired data below consists of test scores and hours of preparation for 5 randomly selected students. The equation of the regression line is . Find the unexplained variation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
71
The paired data below consists of test scores and hours of preparation for 5 randomly selected students. The equation of the regression line is . Find the explained variation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
72
For the data below, determine the logarithmic equation, that best fits the data. Hint: Begin by replacing each -value with then use the usual methods to find the equation of the least squares regression 1
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
73
Solve the problem.
-For the data below, determine the value of the linear correlation coefficient r between y and x2.
A)0.913
B)0.990
C)0.985
D)0.873
-For the data below, determine the value of the linear correlation coefficient r between y and x2.
A)0.913
B)0.990
C)0.985
D)0.873

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
74
For the data below, determine the value of the linear correlation coefficient r between y and ln x and test whether the linear correlation is significant. Use a significance level of 0.05.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
75
A collection of paired data consists of the number of years that students have studied Spanish and their scores on a Spanish language proficiency test. A computer program was used to obtain the least squares linear regression line and the computer output is shown below. Along with the paired sample data, the program was also given an x value of 2 (years of study)to be used for predicting test score. What percentage of the total variation in test scores is unexplained by the linear relationship between years of study and test scores?
A)82.7%
B)83.0%
C)17.0%
D)8.9%
A)82.7%
B)83.0%
C)17.0%
D)8.9%

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
76
A collection of paired data consists of the number of years that students have studied Spanish and their scores on a Spanish language proficiency test. A computer program was used to obtain the least squares linear regression line and the computer output is shown below. Along with the paired sample data, the program was also given an x value of 2 (years of study)to be used for predicting test score.
Predicted values
If a person studies 4.5 years, what is the single value that is the best predicted test score? Assume that there is a significant linear correlation between years of study and test score.
A)53.35
B)80.6
C)83.0
D)49.1
Predicted values
If a person studies 4.5 years, what is the single value that is the best predicted test score? Assume that there is a significant linear correlation between years of study and test score.
A)53.35
B)80.6
C)83.0
D)49.1

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
77
Find the coefficient of determination, given that the value of the linear correlation coefficient, r, is 0.326.
A)0.674
B)0.326
C)0.894
D)0.106
A)0.674
B)0.326
C)0.894
D)0.106

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
78
The following are costs of advertising (in thousands of dollars)and the numbers of products sold (in thousands):
The equation of the regression line is . Find the coefficient of determination.
A)
B)
C)
D)
The equation of the regression line is . Find the coefficient of determination.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
79
The equation of the regression line for the paired data below is . Find the coefficient of determination.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
80
A regression equation is obtained for a collection of paired data. It is found that the total variation is 25.753, the explained variation is 18.658, and the unexplained variation is 7.095. Find the coefficient of determination.
A)0.724
B)1.380
C)0.380
D)0.276
A)0.724
B)1.380
C)0.380
D)0.276

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck



