Deck 3: Triangles
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/16
Play
Full screen (f)
Deck 3: Triangles
1
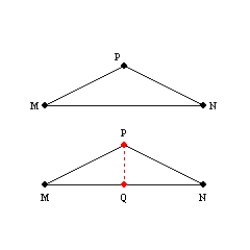
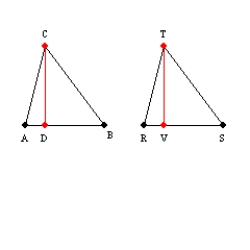
Provide missing statements and missing reasons for the proof of the theorem,
"If two sides of a triangle are congruent, then the angles opposite those sides are
also congruent."
Given:
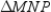 with
with 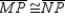 Prove:
Prove: 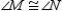 S1. R1.
S1. R1.S2. Draw the angle bisector for
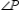 R2. Every angle has exactly one angle-bisector.
R2. Every angle has exactly one angle-bisector.S3.
 R3.
R3.S4. R4.
S1. 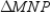 with
with 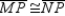 R1. Given
R1. Given
R3. The bisector of the vertex angle of an isosceles triangle separates the triangle into
two congruent triangles.
S4.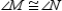 R4. CPCTC
R4. CPCTC
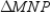 with
with 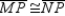 R1. Given
R1. GivenR3. The bisector of the vertex angle of an isosceles triangle separates the triangle into
two congruent triangles.
S4.
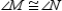 R4. CPCTC
R4. CPCTC 2
Provide mssing statements and missing reasons for the proof of the theorem,
"Corresponding altitudes of congruent triangles are congruent."
Given:
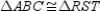 ;
; 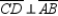 and
and 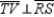 Prove:
Prove: 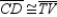 S1.
S1.  R1.
R1.S2.
 and
and  R2.
R2.S3. R3. Given
S4.
 and
and 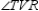 are rt.
are rt.  R4.
R4.S5. R5. All right angles are congruent.
S6.
 R6.
R6.S7. R7.
R1. Given
R2. CPCTC
S3.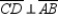 and
and 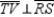 R4. Perpendicular lines form right angles.
R4. Perpendicular lines form right angles.
S5. R6. AAS
R6. AAS
S7.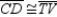 R7. CPCTC
R7. CPCTC
R2. CPCTC
S3.
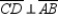 and
and 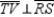 R4. Perpendicular lines form right angles.
R4. Perpendicular lines form right angles.S5.
 R6. AAS
R6. AASS7.
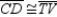 R7. CPCTC
R7. CPCTC 3
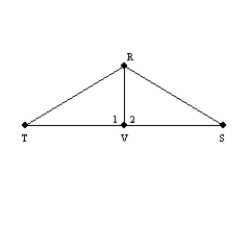
Provide the missing statements and missing reasons for the following proof.
Given:
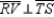 and V is the midpoint of
and V is the midpoint of  Prove:
Prove: 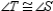 S1.
S1. 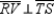 R1.
R1.S2.
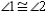 R2.
R2.S3. R3. Given
S4.
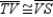 R4.
R4.S5. R5. Identity
S6.
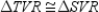 R6.
R6.S7. R7.
R1. Given
R2. Perpendicular lines form congruent adjacent angles.
S3. V is the midpoint of R4. Definition of midpoint
R4. Definition of midpoint
S5.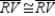 R6. SAS
R6. SAS
S7.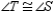 R7. CPCTC
R7. CPCTC
R2. Perpendicular lines form congruent adjacent angles.
S3. V is the midpoint of
 R4. Definition of midpoint
R4. Definition of midpointS5.
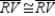 R6. SAS
R6. SASS7.
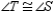 R7. CPCTC
R7. CPCTC 4
In the following problem, explain (prove) why the conclusion is valid..
Given: Quadrilateral
 with diagonal
with diagonal  ;
; 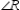 and
and 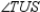 are right angles
are right anglesProve:
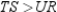

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
5
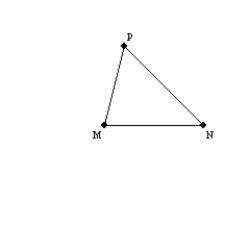
Supply missing statements and missing reasons for the following proof.
Given:
 and
and 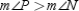 Prove:
Prove: 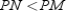 S1. R1.
S1. R1.S2.
 R2. If the measure of one
R2. If the measure of one  of a
of a 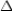 is greater than the measure of a
is greater than the measure of a2nd
 of the
of the 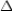 , then the side opposite the larger
, then the side opposite the larger  is longer than
is longer thanthe side opposite the smaller
 .
.S3. R3.

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
6
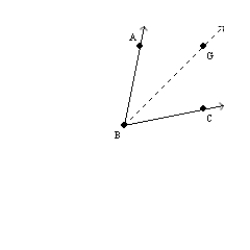
Explain why the angle-bisector method is justified. Consider that the given angle,
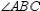 ,
,is to be bisected by the constructed ray,
 .
.
Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
7
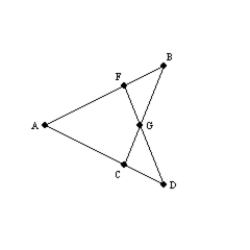
Supply missing statements and missing reasons for the following proof.
Given:
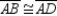 ;
; 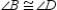 Prove:
Prove: 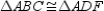 S1.
S1. 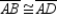 ;
; 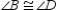 R1.
R1.S2. R2. Identity
S3. R3.

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
8

Supply missing statements and missing reasons for the following proof.
Given:
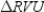 ;
; 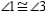 and
and 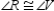 Prove:
Prove:  is an isosceles triangle
is an isosceles triangleS1.
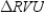 ;
; 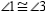 R1.
R1.S2.
 R2.
R2.S3. R3. If 2 angles of a triangle are congruent, the sides
opposite these angles are congruent.
S4.
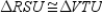 R4.
R4.S5. R5. CPCTC
S6.
 is an isosceles triangle R6.
is an isosceles triangle R6.
Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
9

In the figure provided,
 . Explain why it is necessary that
. Explain why it is necessary that 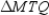 is also
is alsocongruent to
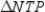

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
10
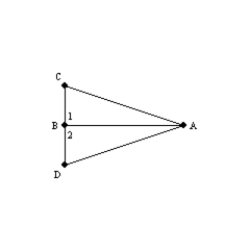
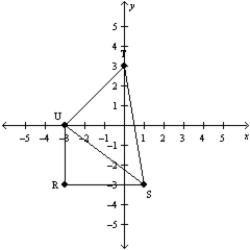
Provide missing statements for the following proof.
Given:
 and
and  are right angles;
are right angles;  Prove:
Prove:  S1. R1. Given
S1. R1. GivenS2. R2. All right angles are congruent.
S3. R3. Identity
S4. R4. SAS
S5. R5. CPCTC

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
11
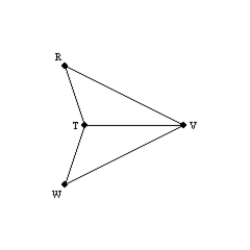
Provide missing reasons for this proof.
Given:
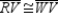 and
and 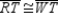 Prove:
Prove: 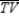 bisects
bisects 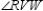 S1.
S1. 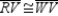 and
and 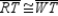 R1.
R1.S2.
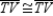 R2.
R2.S3.
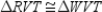 R3.
R3.S4,
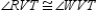 R4.
R4.S5.
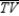 bisects
bisects 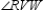 R5.
R5.
Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
12
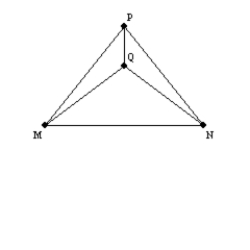
Provide all statements and all reasons for this proof.
Given:
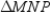 with
with 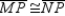 ;
; 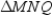 with
with 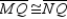 Prove:
Prove: 

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
13
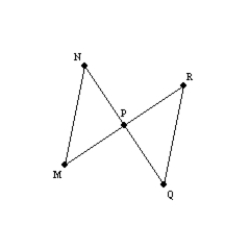
Provide missing statements for the following proof.
Given:
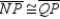 and
and 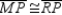 Prove:
Prove:  S1. R1. Given
S1. R1. GivenS2. R2. Vertical angles are congruent.
S3. R3. SAS

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
14
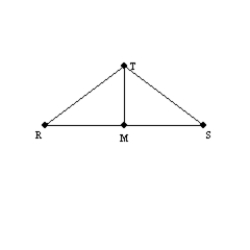
Provide the missing reasons for the following proof.
Given: M is the midpoint of
 ; also,
; also, 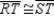 Prove:
Prove: 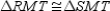 S1. M is the midpoint of
S1. M is the midpoint of  R1.
R1.S2.
 R2.
R2.S3.
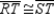 R3.
R3.S4.
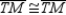 R4.
R4.S5.
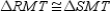 R5.
R5.
Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
15

Provide missing statements and missing reasons for the following proof.
Given:
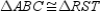 ; M is the midpoint of
; M is the midpoint of 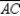 and N is the midpoint of
and N is the midpoint of  Prove:
Prove: 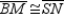 S1.
S1. 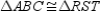 R1.
R1.S2.
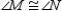 ,
,  , and
, and 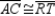 R2.
R2.S3. R3. Given
S4.
 R4. The midpoints of two congruent line segments
R4. The midpoints of two congruent line segmentsdivide the segments into 4 congruent segments.
S5.
 R5.
R5.S6. R6.

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
16

Use the given drawing and information to prove Theorem 3.1.1 (AAS). Provide all
statements and reasons.
Given:
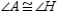 ,
, 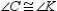 , and
, and 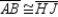 Prove:
Prove: 

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck



