Deck 6: Circles
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/10
Play
Full screen (f)
Deck 6: Circles
1
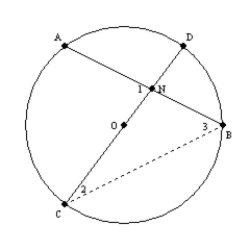
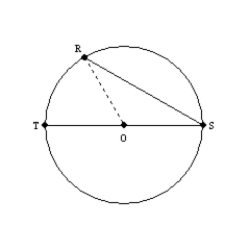
Supply missing statements and missing reasons for the following proof.
Given: Chords
 and
and  intersect at point N in
intersect at point N in  Prove:
Prove: 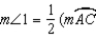
 )
)S1. R1.
S2. Draw
 R2.
R2.S3.
 R3. The measure of an ext.
R3. The measure of an ext.  of a
of a  is
is  the sum
the sumof measures of the two nonadjacent int.
 . S4.
. S4. 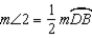 and
and 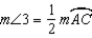 R4.
R4.S5. R5. Substitution Property of Equality
S6. R6. Substitution Property of Equality
S1. Chords 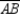 and
and 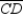 intersect at point N in
intersect at point N in 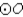 R1. Given
R1. Given
R2. Through 2 points, there is exactly one line.
R4. In a circle, the measure of an inscribed angle is one-half that of its intercepted arc.
S5.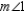
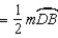
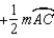 S6.
S6. 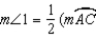
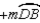 )
)
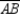 and
and 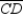 intersect at point N in
intersect at point N in  R1. Given
R1. GivenR2. Through 2 points, there is exactly one line.
R4. In a circle, the measure of an inscribed angle is one-half that of its intercepted arc.
S5.
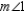
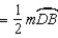
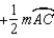 S6.
S6. 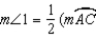
 )
) 2
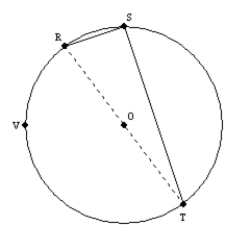
Supply missing statements and missing reasons for the proof of the following theorem.
"An angle inscribed in a semicircle is a right angle."
Given:
 with diameter
with diameter  and
and  (as shown)
(as shown)Prove:
 is a right angle.
is a right angle.S1. R1.
S2.
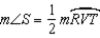 R2.
R2.S3. R3. The measure of a semicircle is 180.
S4.
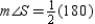 or
or 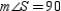 R4.
R4.S5. R5.
S1. 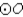 with diameter
with diameter  and
and  (as shown)
(as shown)
R1. Given
R2. The measure of an inscribed angle is on-half the degree measure of its intercepted arc.
S3.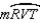
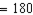 R4. Substitution Property of Equality
R4. Substitution Property of Equality
S5. is a right angle.
is a right angle.
R5. Definition of a right angle.
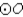 with diameter
with diameter  and
and  (as shown)
(as shown)R1. Given
R2. The measure of an inscribed angle is on-half the degree measure of its intercepted arc.
S3.
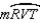
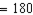 R4. Substitution Property of Equality
R4. Substitution Property of EqualityS5.
 is a right angle.
is a right angle.R5. Definition of a right angle.
3
![Use the drawing provided to explain why the following theorem is true. The tangent segments to a circle from an external point are congruent. Given: and are tangent to Prove: [Hint: Use auxiliary line segment .]](https://d2lvgg3v3hfg70.cloudfront.net/TB7237/11eb4b36_76fe_33df_a05a_55181bd3fd53_TB7237_11.jpg)
Use the drawing provided to explain why the following theorem is true.
"The tangent segments to a circle from an external point are congruent."
Given:
![Use the drawing provided to explain why the following theorem is true. The tangent segments to a circle from an external point are congruent. Given: and are tangent to Prove: [Hint: Use auxiliary line segment .]](https://d2lvgg3v3hfg70.cloudfront.net/TB7237/11eb4b36_76fe_33e0_a05a_e760851bebfb_TB7237_11.jpg) and
and ![Use the drawing provided to explain why the following theorem is true. The tangent segments to a circle from an external point are congruent. Given: and are tangent to Prove: [Hint: Use auxiliary line segment .]](https://d2lvgg3v3hfg70.cloudfront.net/TB7237/11eb4b36_76fe_5af1_a05a_e35fffdaf6a0_TB7237_11.jpg) are tangent to
are tangent to ![Use the drawing provided to explain why the following theorem is true. The tangent segments to a circle from an external point are congruent. Given: and are tangent to Prove: [Hint: Use auxiliary line segment .]](https://d2lvgg3v3hfg70.cloudfront.net/TB7237/11eb4b36_76fe_5af2_a05a_338c546d8311_TB7237_11.jpg) Prove:
Prove: ![Use the drawing provided to explain why the following theorem is true. The tangent segments to a circle from an external point are congruent. Given: and are tangent to Prove: [Hint: Use auxiliary line segment .]](https://d2lvgg3v3hfg70.cloudfront.net/TB7237/11eb4b36_76fe_5af3_a05a_d103c5d080c0_TB7237_11.jpg) [Hint: Use auxiliary line segment
[Hint: Use auxiliary line segment ![Use the drawing provided to explain why the following theorem is true. The tangent segments to a circle from an external point are congruent. Given: and are tangent to Prove: [Hint: Use auxiliary line segment .]](https://d2lvgg3v3hfg70.cloudfront.net/TB7237/11eb4b36_76fe_5af4_a05a_2532aeee0240_TB7237_11.jpg) .]
.]Draw 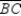 . Now
. Now 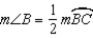 and
and 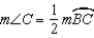 because the measure of an angle formed by a tangent and chord at the point of contact is one-half the measure of the intercepted arc.
because the measure of an angle formed by a tangent and chord at the point of contact is one-half the measure of the intercepted arc.
Then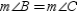 by substitution, so
by substitution, so 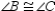 . Then
. Then 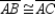 because these sides lie opposite the congruent angles of
because these sides lie opposite the congruent angles of 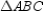 .
.
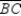 . Now
. Now  and
and  because the measure of an angle formed by a tangent and chord at the point of contact is one-half the measure of the intercepted arc.
because the measure of an angle formed by a tangent and chord at the point of contact is one-half the measure of the intercepted arc.Then
 by substitution, so
by substitution, so 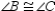 . Then
. Then 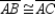 because these sides lie opposite the congruent angles of
because these sides lie opposite the congruent angles of 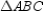 .
. 4
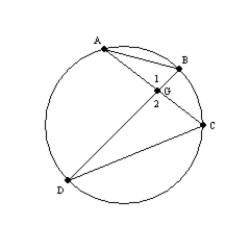
Supply missing statements and missing reasons for the following proof.
Given: Chords
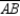 ,
, 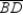 ,
,  , and
, and 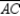 as shown
as shownProve:
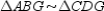 S1. R1.
S1. R1.S2.
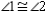 R2.
R2.S3. R3. If 2 inscribed
 intercept the same arc, these
intercept the same arc, these  are
are 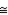 .
.S4. R4.

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
5
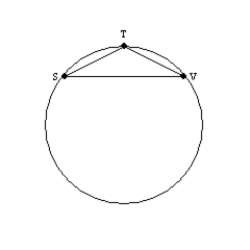
Supply missing statements and missing reasons for the following proof.
Given:
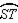
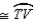 in
in 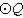 Prove:
Prove: 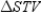 is an isosceles triangle
is an isosceles triangleS1. R1.
S2.
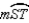
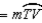 R2.
R2.S3.
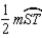
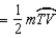 R3.
R3.S4. ? and ? R4. The degree measure of an iscribed angle is equal to one-half
the degree measure of its intercepted arc.
S5.
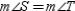 R5.
R5.S6. R6. Definition of congruent angles
S7. R7. If two angles of a triangle are congruent, then the two sides
that lie opposite those angles are also congruent.
S8. R8.

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
6
Supply missing reasons for the following proof.
Given:
 with diameter
with diameter  Prove:
Prove:  S1.
S1. 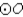 with diameter
with diameter  R1.
R1.S2. Draw radius
 R2.
R2.S3.
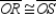 R3.
R3.S4.
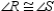 R4.
R4.S5.
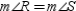 R5.
R5.S6.
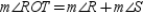 R6.
R6.S7.
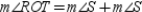 or R7.
or R7. 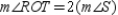 S8.
S8. 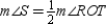 R8.
R8.S9. But
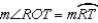 R9.
R9.S10. Then
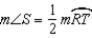 R10.
R10.
Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
7
Explain why the following must be true.
Given: Points A, B, and C lie on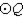 in such a way that
in such a way that 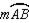
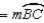 ;
;
also, chords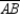 ,
, 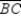 , and
, and 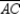 (no drawing provided)
(no drawing provided)
Prove: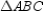 must be an isosceles triangle.
must be an isosceles triangle.
Given: Points A, B, and C lie on
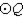 in such a way that
in such a way that 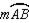
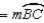 ;
;also, chords
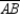 ,
,  , and
, and  (no drawing provided)
(no drawing provided)Prove:
 must be an isosceles triangle.
must be an isosceles triangle.
Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
8
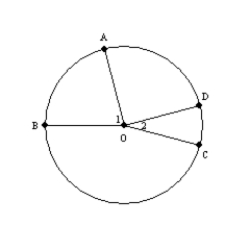
Supply all statements and all reasons for the proof that follows.
Given:
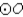 ;
; 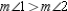 Prove:
Prove: 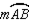
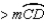

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
9
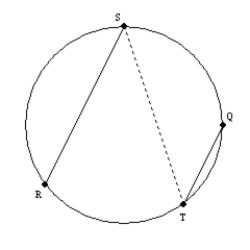
Supply missing statements and missing reasons for the following proof.
Given: In the circle,
 Prove:
Prove: 
 S1. R1.
S1. R1.S2. Draw
 R2.
R2.S3.
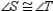 R3.
R3.S4. R4. Congruent angles have equal measures.
S5. ? and ? R5. The measure of an inscribed angle equals one-half
the measure of its intercepted arc.
S6.
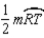
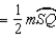 R6.
R6.S7.
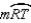
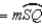 R7.
R7.S8. R8.

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
10
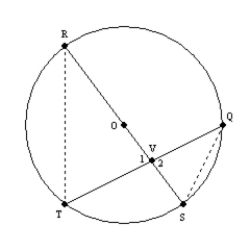
Supply missing statements and missing reasons for the following proof.
Given:
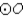 ; chords
; chords  and
and 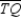 intersect at point V
intersect at point VProve:
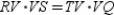 S1. R1.
S1. R1.S2. Draw
 and
and 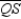 . R2.
. R2.S3. R3. Vertical angles are congruent.
S4.
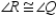 R4.
R4.S5. R5. AA
S6.
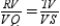 R6.
R6.S7. R7. Means-Extremes Property of a Proportion

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck



