Deck 11: Introduction to Trigonometry
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/4
Play
Full screen (f)
Deck 11: Introduction to Trigonometry
1
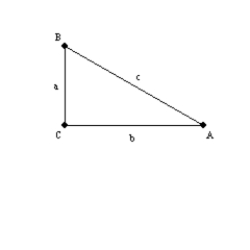
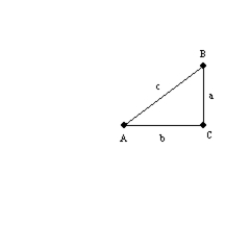
For the right triangle
 with right
with right  , prove that
, prove that 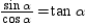 .
.By definition, 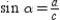 ,
, 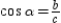 , and
, and 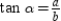 . Then
. Then 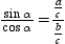 , which can also be written
, which can also be written 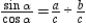 . Then
. Then 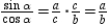 . Thus,
. Thus, 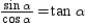 .
.
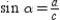 ,
, 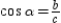 , and
, and 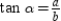 . Then
. Then 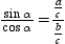 , which can also be written
, which can also be written 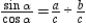 . Then
. Then 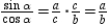 . Thus,
. Thus, 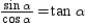 .
. 2
For the right triangle
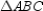 with right
with right  , prove that
, prove that 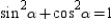 . Note that
. Note that 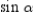 and
and 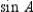 are the same and that
are the same and that 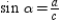 as shown in
as shown in 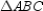 ; also,
; also, 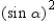 and
and 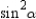 have the
have thesame meaning.
With 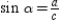 and
and 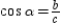 , we see that
, we see that 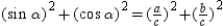 or
or 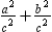 .
.
Then . By using the Pythagorean Theorem, we know that
. By using the Pythagorean Theorem, we know that 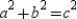 . It follows that
. It follows that 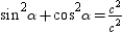 , so
, so 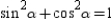 .
.
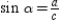 and
and 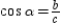 , we see that
, we see that 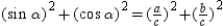 or
or 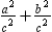 .
.Then
 . By using the Pythagorean Theorem, we know that
. By using the Pythagorean Theorem, we know that 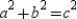 . It follows that
. It follows that 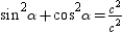 , so
, so 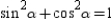 .
. 3
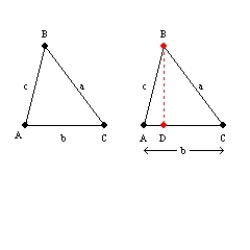
Use the drawings provided to prove the following theorem.
"The area of an acute triangle equals one-half the product of the lengths of two sides of a triangle and the sine of the included angle."
Given: Acute
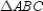 Prove:
Prove: 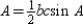
The area of 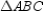 is given by
is given by 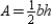 . Considering the auxiliary altitude
. Considering the auxiliary altitude 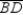 from vertex B
from vertex B
to side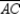 , we see that
, we see that 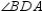 is a right angle. Then
is a right angle. Then 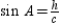 in right triangle
in right triangle 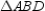 .
.
From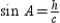 , it follows that
, it follows that 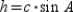 . By substitution, the area formula
. By substitution, the area formula 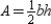 becomes
becomes 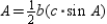 so we have
so we have 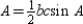 .
.
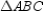 is given by
is given by 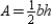 . Considering the auxiliary altitude
. Considering the auxiliary altitude 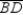 from vertex B
from vertex Bto side
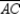 , we see that
, we see that 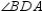 is a right angle. Then
is a right angle. Then 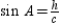 in right triangle
in right triangle 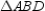 .
.From
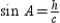 , it follows that
, it follows that 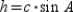 . By substitution, the area formula
. By substitution, the area formula 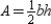 becomes
becomes 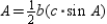 so we have
so we have 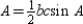 .
. 4
For the right triangle
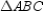 with right
with right  , prove that
, prove that 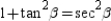 .
.
Unlock Deck
Unlock for access to all 4 flashcards in this deck.
Unlock Deck
k this deck



