Deck 8: Areas of Polygons and Circles
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/5
Play
Full screen (f)
Deck 8: Areas of Polygons and Circles
1
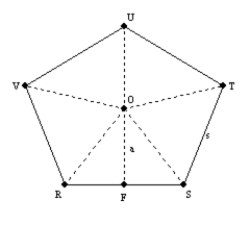
Use the drawing provided to explain the following theorem.
"The area A of a regular polygon whose apothem has length a and whose perimeter
is P is given by
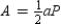 ."
."Given: Regular polygon
 with center O and length s for each side;
with center O and length s for each side;apothem
 so that
so that 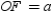 Prove:
Prove: 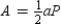
From center O, we draw radii  ,
,  ,
,  ,
,  , and
, and  . Because the radii are congruent to each other and the sides of the regular polygon are all congruent to each other as well,
. Because the radii are congruent to each other and the sides of the regular polygon are all congruent to each other as well, 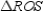 ,
, 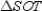 ,
,  ,
, 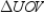 , and
, and 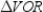 are all congruent to each other by SSS.
are all congruent to each other by SSS.
Each of the congruent triangles has an altitude length of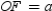 . Further, the length of each
. Further, the length of each
base of a triangle is s, the length of side of the polygon. Therefore, the area of the regular polygon is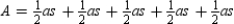
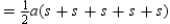 Because the sum of the sides equals perimeter P, we have
Because the sum of the sides equals perimeter P, we have 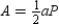 .
.
 ,
,  ,
,  ,
,  , and
, and  . Because the radii are congruent to each other and the sides of the regular polygon are all congruent to each other as well,
. Because the radii are congruent to each other and the sides of the regular polygon are all congruent to each other as well, 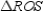 ,
, 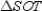 ,
,  ,
, 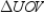 , and
, and 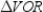 are all congruent to each other by SSS.
are all congruent to each other by SSS.Each of the congruent triangles has an altitude length of
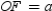 . Further, the length of each
. Further, the length of eachbase of a triangle is s, the length of side of the polygon. Therefore, the area of the regular polygon is
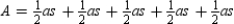
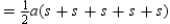 Because the sum of the sides equals perimeter P, we have
Because the sum of the sides equals perimeter P, we have 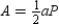 .
. 2
![Where is the degree measure for the arc of a sector of a circle, the ratio of the area of the sector to that of the area of the circle is given by . Use this ratio to explain why the area of the sector is given by . [Note: In the figure, the sector with arc measure is bounded by radii , , and .]](https://d2lvgg3v3hfg70.cloudfront.net/TB7237/11eb4b36_76f8_b5de_a05a_5ff1fb069e11_TB7237_11.jpg)
Where
![Where is the degree measure for the arc of a sector of a circle, the ratio of the area of the sector to that of the area of the circle is given by . Use this ratio to explain why the area of the sector is given by . [Note: In the figure, the sector with arc measure is bounded by radii , , and .]](https://d2lvgg3v3hfg70.cloudfront.net/TB7237/11eb4b36_76f8_b5df_a05a_bdad4d39a492_TB7237_11.jpg) is the degree measure for the arc of a sector of a circle, the ratio of the area of the sector to that of the area of the circle is given by
is the degree measure for the arc of a sector of a circle, the ratio of the area of the sector to that of the area of the circle is given by ![Where is the degree measure for the arc of a sector of a circle, the ratio of the area of the sector to that of the area of the circle is given by . Use this ratio to explain why the area of the sector is given by . [Note: In the figure, the sector with arc measure is bounded by radii , , and .]](https://d2lvgg3v3hfg70.cloudfront.net/TB7237/11eb4b36_76f8_dbf0_a05a_11cf37c67e76_TB7237_11.jpg) . Use this ratio to explain why
. Use this ratio to explain whythe area of the sector is given by
![Where is the degree measure for the arc of a sector of a circle, the ratio of the area of the sector to that of the area of the circle is given by . Use this ratio to explain why the area of the sector is given by . [Note: In the figure, the sector with arc measure is bounded by radii , , and .]](https://d2lvgg3v3hfg70.cloudfront.net/TB7237/11eb4b36_76f8_dbf1_a05a_d3ebdcf512c0_TB7237_11.jpg) .
.[Note: In the figure, the sector with arc measure
![Where is the degree measure for the arc of a sector of a circle, the ratio of the area of the sector to that of the area of the circle is given by . Use this ratio to explain why the area of the sector is given by . [Note: In the figure, the sector with arc measure is bounded by radii , , and .]](https://d2lvgg3v3hfg70.cloudfront.net/TB7237/11eb4b36_76f8_dbf2_a05a_3bca88e0264e_TB7237_11.jpg) is bounded by radii
is bounded by radii ![Where is the degree measure for the arc of a sector of a circle, the ratio of the area of the sector to that of the area of the circle is given by . Use this ratio to explain why the area of the sector is given by . [Note: In the figure, the sector with arc measure is bounded by radii , , and .]](https://d2lvgg3v3hfg70.cloudfront.net/TB7237/11eb4b36_76f8_dbf3_a05a_3f329bab93d1_TB7237_11.jpg) ,
, ![Where is the degree measure for the arc of a sector of a circle, the ratio of the area of the sector to that of the area of the circle is given by . Use this ratio to explain why the area of the sector is given by . [Note: In the figure, the sector with arc measure is bounded by radii , , and .]](https://d2lvgg3v3hfg70.cloudfront.net/TB7237/11eb4b36_76f8_dbf4_a05a_57185d1953d0_TB7237_11.jpg) , and
, and ![Where is the degree measure for the arc of a sector of a circle, the ratio of the area of the sector to that of the area of the circle is given by . Use this ratio to explain why the area of the sector is given by . [Note: In the figure, the sector with arc measure is bounded by radii , , and .]](https://d2lvgg3v3hfg70.cloudfront.net/TB7237/11eb4b36_76f8_dbf5_a05a_1f8c81ba26c7_TB7237_11.jpg) .]
.]Given that 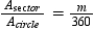 , it follows that
, it follows that 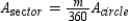 . Where r is the length of radius of the circle, the area of the circle is given by
. Where r is the length of radius of the circle, the area of the circle is given by 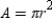 . By substitution, it follows that
. By substitution, it follows that 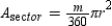 .
.
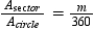 , it follows that
, it follows that 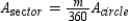 . Where r is the length of radius of the circle, the area of the circle is given by
. Where r is the length of radius of the circle, the area of the circle is given by 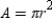 . By substitution, it follows that
. By substitution, it follows that 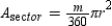 .
. 3
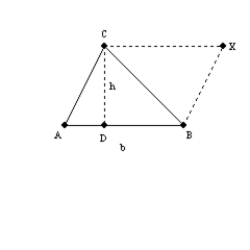
Using the drawing provided and fact that the area of a parallelogram is given by
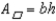 , show that the area of a triangle is given by
, show that the area of a triangle is given by 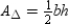 .
.For the parallelogram ( 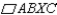 ) with base length b and altitude length h, the area is given by
) with base length b and altitude length h, the area is given by 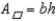 . By the Area-Addition Postulate,
. By the Area-Addition Postulate, 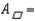
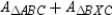 . But diagonal
. But diagonal  of
of 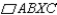 separates the parallelogram into 2 congruent triangles that have equal areas.
separates the parallelogram into 2 congruent triangles that have equal areas.
By substitution,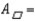
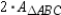 and by division (or multiplication),
and by division (or multiplication), 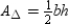 .
.
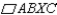 ) with base length b and altitude length h, the area is given by
) with base length b and altitude length h, the area is given by 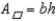 . By the Area-Addition Postulate,
. By the Area-Addition Postulate, 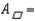
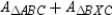 . But diagonal
. But diagonal  of
of 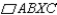 separates the parallelogram into 2 congruent triangles that have equal areas.
separates the parallelogram into 2 congruent triangles that have equal areas.By substitution,
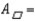
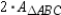 and by division (or multiplication),
and by division (or multiplication), 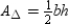 .
. 4
Consider a circle with diameter length d, radius length r, and circumference C. Given that 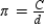 , explain why the formula for the circumference of a circle is given by
, explain why the formula for the circumference of a circle is given by  .
.
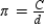 , explain why the formula for the circumference of a circle is given by
, explain why the formula for the circumference of a circle is given by  .
.
Unlock Deck
Unlock for access to all 5 flashcards in this deck.
Unlock Deck
k this deck
5
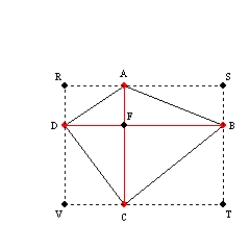
Use the drawing provided to explain the following theorem.
"The area of any quadrilateral with perpendicular diagonals of lengths
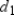 and
and 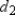 is given by
is given by  ."
."Given: Quadrilateral
 with
with 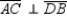 at point F;
at point F; 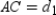 and
and 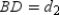 Prove:
Prove: 

Unlock Deck
Unlock for access to all 5 flashcards in this deck.
Unlock Deck
k this deck



