Deck 7: Locus and Concurrence
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/4
Play
Full screen (f)
Deck 7: Locus and Concurrence
1
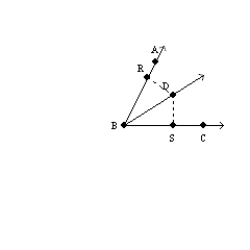
Supply missing reasons for the following proof.
Given:
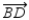 bisects
bisects  ;
; 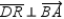 and
and 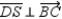 Prove:
Prove:  S1.
S1.  bisects
bisects 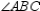 ; R1.
; R1. 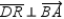 and
and 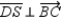 S2.
S2. 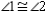 R2.
R2.S3.
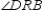 and
and 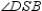 are rt.
are rt.  R3.
R3.S4.
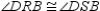 R4.
R4.S5.
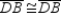 R5.
R5.S6.
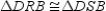 R6.
R6.S7.
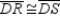 R7.
R7.R1. Given
R2. Definition of angle-bisector
R3. Perpendicular lines form right angles.
R4. All right angles are congruent.
R5. Identity
R6. AAS
R7. CPCTC
R2. Definition of angle-bisector
R3. Perpendicular lines form right angles.
R4. All right angles are congruent.
R5. Identity
R6. AAS
R7. CPCTC
2
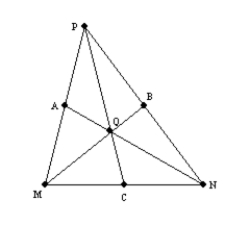
Use the drawing provided to explain the following.
Given:
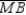 ,
, 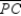 , and
, and 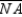 are the medians of
are the medians of 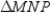 Prove:
Prove: 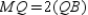
If 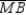 ,
, 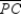 , and
, and 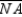 are the medians of
are the medians of 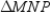 , then their point of concurrence is
, then their point of concurrence is
Q, the centroid of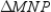 . It follows that
. It follows that 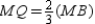 . By the Segment-Addition
. By the Segment-Addition
Postulate, we have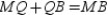 . By substitution,
. By substitution,  . By subtraction,
. By subtraction, 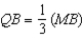 . In turn,
. In turn, 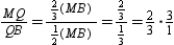 or 2. Multiplying the equation
or 2. Multiplying the equation 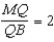 by
by 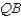 , we have
, we have 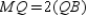 .
.
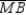 ,
, 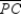 , and
, and 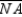 are the medians of
are the medians of 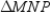 , then their point of concurrence is
, then their point of concurrence isQ, the centroid of
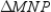 . It follows that
. It follows that 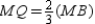 . By the Segment-Addition
. By the Segment-AdditionPostulate, we have
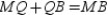 . By substitution,
. By substitution,  . By subtraction,
. By subtraction, 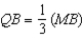 . In turn,
. In turn, 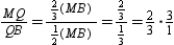 or 2. Multiplying the equation
or 2. Multiplying the equation 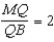 by
by 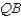 , we have
, we have 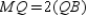 .
. 3
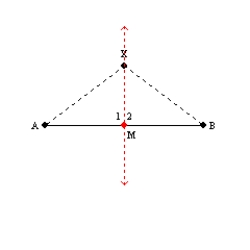
Supply missing statements and missing reasons for the following proof.
Given: Point X not on
 so that
so that 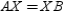 Prove: X lies on the perpendicular-bisector of
Prove: X lies on the perpendicular-bisector of 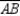 S1. R1.
S1. R1.S2.
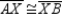 R2.
R2.S3. With M the midpoint of
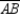 , R3.
, R3.draw
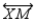 S4. Then
S4. Then  R4.
R4.S5. Also,
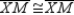 R5.
R5.S6. R6. SSS
S7.
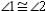 R7.
R7.S8. R8. Definition of perpendicular-bisector of a line segment
S1. Point X not on  so that
so that 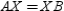 R1. Given
R1. Given
R2. Definition of congruent line segments
R3. Through 2 points, there is exactly one line.
R4. Definition of midpoint of line segment
R5. Identity
S6.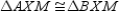 R7. CPCTC
R7. CPCTC
S8. X lies on the perpendicular-bisector of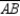
 so that
so that 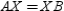 R1. Given
R1. GivenR2. Definition of congruent line segments
R3. Through 2 points, there is exactly one line.
R4. Definition of midpoint of line segment
R5. Identity
S6.
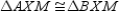 R7. CPCTC
R7. CPCTCS8. X lies on the perpendicular-bisector of
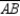
4
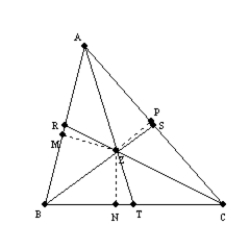
Use the drawing provided to explain the following theorem.
"The three angle bisectors of the angles of a triangle are concurrent."
Given:
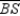 ,
,  , and
, and  are the angle bisectors of the angles of
are the angle bisectors of the angles of 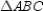 Prove:
Prove:  ,
,  , and
, and  are concurrent at point Z
are concurrent at point Z
Unlock Deck
Unlock for access to all 4 flashcards in this deck.
Unlock Deck
k this deck



