Deck 16: Series and Taylor Polynomials Web
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/127
Play
Full screen (f)
Deck 16: Series and Taylor Polynomials Web
1
Find the indicated term of the sequence.
A)-44
B)47
C)49
D)-2
E)45
A)-44
B)47
C)49
D)-2
E)45
47
2
Determine whether the sequence is arithmetic. If so, find the common difference. (Assume that n begins with 1.)
A)7
B)2
C)-2
D)-7
E)not arithmetic
A)7
B)2
C)-2
D)-7
E)not arithmetic
-7
3
Determine whether the sequence is arithmetic. If so, find the common difference. 2, 1, 0, -1, -2
A)3
B)-1
C)2
D)1
E)not arithmetic
A)3
B)-1
C)2
D)1
E)not arithmetic
-1
4
Determine whether the sequence is arithmetic. If so, find the common difference. 3, 9, 27, 81, 243
A)3
B)3n
C)3n - 3n-1
D)-3
E)not arithmetic
A)3
B)3n
C)3n - 3n-1
D)-3
E)not arithmetic

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
5
Write an expression for the most apparent nth term of the sequence. (Assume that begins with 1.)
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
6
A deposit of $2000 is made in an account that earns 6% interest compounded monthly. The balance in the account after n months is given by Find the balance in the account after 11 years by finding the 132th term of the sequence. Round to the nearest penny.
A)$4,379,295.09
B)$3863.23
C)$3844.01
D)$265,320.00
E)$3882.54
A)$4,379,295.09
B)$3863.23
C)$3844.01
D)$265,320.00
E)$3882.54

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
7
Write an expression for the apparent nth term of the sequence. (Assume that n begins with 1.) 9, 12, 15, 18, 21
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
8
Write the first five terms of the sequence. (Assume that n begins with 1.)
A)-4, -1, 2, 5, 8
B)7, 10, 13, 16, 19
C)10, 6, 9, 12, 15
D)10, 13, 16, 19, 22
E)10, 17, 24, 31, 38
A)-4, -1, 2, 5, 8
B)7, 10, 13, 16, 19
C)10, 6, 9, 12, 15
D)10, 13, 16, 19, 22
E)10, 17, 24, 31, 38

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
9
Find the fifth term of the sequence that has the given nth term.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
10
Evaluate the series.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
11
Suppose the ratio of alligators to pythons in a marshland from 2001 to 2008 can be approximated by the model where is the year, with corresponding to In 2006, the total number of alligators and pythons in the marsh was about 900. In that year, how many were pythons?
A)848
B)55
C)844
D)52
E)845
A)848
B)55
C)844
D)52
E)845

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
12
Match the sequence with the graph of its first 10 terms.
A)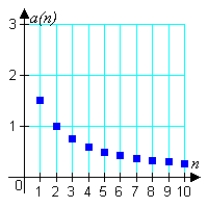
B)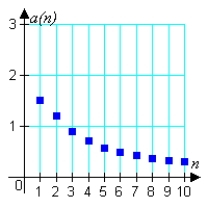
C)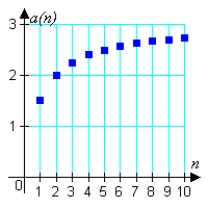
D)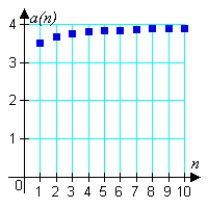
E)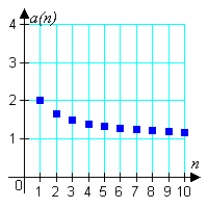
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
13
Write an expression for the apparent nth term of the sequence. (Assume that n begins with 1.)
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
14
Find a formula for an for the arithmetic sequence.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
15
Suppose that the annual payroll (in billions of dollars) of new car dealerships in the United States from 2000 to 2005 can be approximated by the model where represents the year, with corresponding to 2000. Find the total payroll from 2000 to 2005 by evaluating the sum Round your answer to the nearest ten million dollars.
A)$334.78 billion
B)$284.91 billion
C)$377.86 billion
D)$290.08 billion
E)$235.36 billion
A)$334.78 billion
B)$284.91 billion
C)$377.86 billion
D)$290.08 billion
E)$235.36 billion

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
16
Write the given series in summation notation.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
17
Simplify the factorial expression.
A)2184
B)182
C)
D)14
E)2730
A)2184
B)182
C)
D)14
E)2730

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
18
Find the sum.
A)-1
B)-2
C)3
D)4
E)18
A)-1
B)-2
C)3
D)4
E)18

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
19
Write the given series in summation notation.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
20
Determine whether the sequence is arithmetic. If so, find the common difference. (Assume that n begins with 1.)
A)-8
B)5
C)
D)8
E)not arithmetic
A)-8
B)5
C)
D)8
E)not arithmetic

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
21
The annual sales (in millions of dollars) for a certain company from 2001 to 2006 can be approximated by the model where represents the year, with corresponding to 2001. Find the total sales from 2001 to 2004. Round to the nearest million.
A)$2972 million
B)$4119 million
C)$1987 million
D)$2229 million
E)$1502 million
A)$2972 million
B)$4119 million
C)$1987 million
D)$2229 million
E)$1502 million

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
22
Find the sum of the integers from 5 to 27.
A)378
B)22
C)736
D)368
E)756
A)378
B)22
C)736
D)368
E)756

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
23
Determine whether the sequence is geometric. If so, find the common ratio. 1, -3, 9, -27, ...
A)-3
B)1
C)
D)3
E)not geometric
A)-3
B)1
C)
D)3
E)not geometric

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
24
The seating section in a theater has 29 seats in the first row, 34 seats in the second row, and so on, increasing by 5 seats each row for a total of 15 rows. How many seats are in the thirteenth row?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
25
Use summation notation to write the sum below.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
26
Match the arithmetic sequence with its graph from the choices below.
A)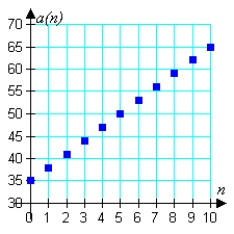
B)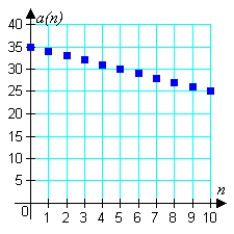
C)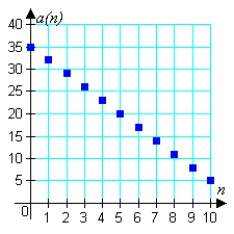
D)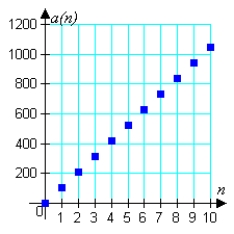
E)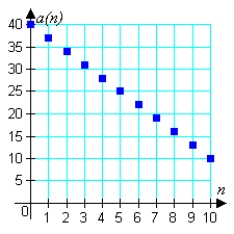
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
27
Find a formula for for the arithmetic sequence below.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
28
Find the indicated nth term of the geometric sequence. 7th term:
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
29
Determine whether the sequence is geometric. If so, find the common ratio. 5, 7, 9, 11, ...
A)2
B)5
C)
D)-2
E)not geometric
A)2
B)5
C)
D)-2
E)not geometric

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
30
Find the indicated nth partial sum of the arithmetic sequence. 3.4, 6.2, 9, 11.8, ..., n = 10
A)181
B)188
C)160
D)159.4
E)160.6
A)181
B)188
C)160
D)159.4
E)160.6

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
31
A heavy object (with negligible air resistance) is dropped from a plane. During the first second of fall, the object falls 17.4 meters; during the second second, it falls 52.2 meters; during the third second, it falls 87.0 meters; and during the fourth second, it falls 121.8 meters. If this pattern continues, how many meters will the object fall in 10 seconds?
A)2505.6 meters
B)1409.4 meters
C)626.4 meters
D)1740.0 meters
E)852.6 meters
A)2505.6 meters
B)1409.4 meters
C)626.4 meters
D)1740.0 meters
E)852.6 meters

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
32
Find the partial sum.
A)-39,339
B)-38,781
C)-39,620
D)-39,903
E)-39,340
A)-39,339
B)-38,781
C)-39,620
D)-39,903
E)-39,340

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
33
Match the geometric sequence with its graph from the choices below.
A)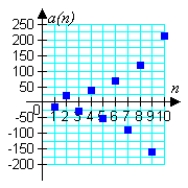
B)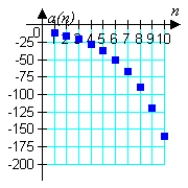
C)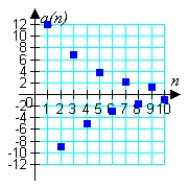
D)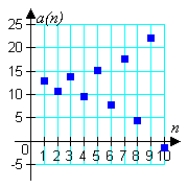
E)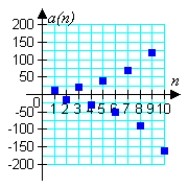
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
34
Use a graphing utility to graph the first 10 terms of the sequence.
A)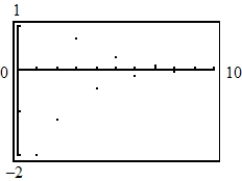
B)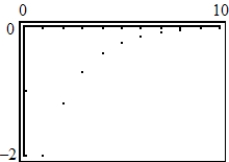
C)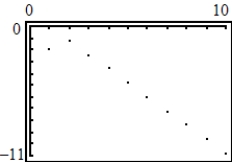
D)
E)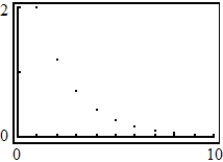
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
35
Find the nth term of the geometric sequence.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
36
Write the first five terms of the arithmetic sequence.
A)-5, -11, -17, -23, -29
B)1, 7, 13, 19, 25
C)-5, 1, 7, 13, 19
D)-5, -30, -180, -1080, -6480
E)-5, 1, -4, -9, -14
A)-5, -11, -17, -23, -29
B)1, 7, 13, 19, 25
C)-5, 1, 7, 13, 19
D)-5, -30, -180, -1080, -6480
E)-5, 1, -4, -9, -14

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
37
Write the first five terms of the geometric sequence.
A)-1, -7, -13, -19, -25
B)-1, 6, -36, 216, -1296
C)
D)
E)
A)-1, -7, -13, -19, -25
B)-1, 6, -36, 216, -1296
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
38
Find the nth term of the geometric sequence.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
39
Logs are stacked so that there are 17 logs in the bottom row, 16 logs in the second row from the bottom, and so on, decreasing by 1 log each row. How many logs are there in the first five rows from the bottom?
A)117 logs
B)108 logs
C)75 logs
D)87 logs
E)125 logs
A)117 logs
B)108 logs
C)75 logs
D)87 logs
E)125 logs

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
40
Consider a job offer with a starting salary of $43,200 and a given annual raise of $2175. Determine the total compensation from the company through seven full years of employment.
A)$406,500
B)$291,825
C)$185,850
D)$136,125
E)$348,075
A)$406,500
B)$291,825
C)$185,850
D)$136,125
E)$348,075

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
41
Write an expression for the nth term of the sequence .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
42
Find the sum of the finite geometric series. Round to the nearest hundredth.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
43
Find the rational number representation of the repeating decimal.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
44
Write the first five terms of the sequence. an =
A)
B)
C)
D)
E)none of the above
A)
B)
C)
D)
E)none of the above

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
45
Determine the convergence or divergence of the sequence . If the sequence converges, use a symbolic algebra utility to find its limit.
A)9
B)4
C)5
D)
E)The sequence diverges.
A)9
B)4
C)5
D)
E)The sequence diverges.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
46
Find the sum of the finite geometric series.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
47
Use summation notation to write the sum.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
48
Write an expression for the nth term of the sequence 2, 8, 26, 80, ....
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
49
Find the limit of the sequence .
A)
B)
C)
D)
E)The sequence diverges.
A)
B)
C)
D)
E)The sequence diverges.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
50
Write the first five terms of the sequence. an =
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
51
Find the limit of the following sequence.
A)
B)
C)
D)
E)The sequence diverges.
A)
B)
C)
D)
E)The sequence diverges.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
52
Find the sum of the finite geometric sequence.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
53
Find the limit of the following sequence.
A)3
B)1
C)
D)-3
E)The sequence diverges.
A)3
B)1
C)
D)-3
E)The sequence diverges.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
54
The annual profit (in millions of dollars) for a certain company from 2000 to 2005 can be approximated by the model where represents the year, with corresponding to 2000. Use the formula for the sum of a finite geometric sequence to approximate the total profit earned during this six-year period. Round to the nearest ten-thousand dollars.
A)$3810.36 million
B)$4112.94 million
C)$3132.16 million
D)$2829.58 million
E)$2325.95 million
A)$3810.36 million
B)$4112.94 million
C)$3132.16 million
D)$2829.58 million
E)$2325.95 million

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
55
Write the rational number as the quotient of two integers in simplest form.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
56
Find the sum of the infinite geometric series.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
57
Write an expression for the nth term of the sequence.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
58
Find the sum of the infinite geometric series below.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
59
Find the sum of the infinite geometric series.
A)
B)
C)
D)
E)undefined
A)
B)
C)
D)
E)undefined

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
60
Find the limit of the following sequence.
A)
B)1
C)2
D)
E)The sequence diverges.
A)
B)1
C)2
D)
E)The sequence diverges.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
61
The repeating decimal is expressed as a geometric series . Write the decimal as the ratio of two integers.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
62
A deposit of 200 is made each month in an account that earns 8.4% interest, compounded monthly. The balance in the account after n months is given by . Find the balance after 22 years by computing the 264th term of the sequence. Round your answer to two decimal places.
A)$213,316.53
B)$293,716.53
C)$6,667.78
D)$86,634.61
E)$281.40
A)$213,316.53
B)$293,716.53
C)$6,667.78
D)$86,634.61
E)$281.40

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
63
A ball is dropped from a height of 14 feet, and on each rebound it rises to its preceding height. Write an expression for the height of the nth rebound.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
64
Find the sum of the convergent series.
A)
B)
C)
D)9
E)8
A)
B)
C)
D)9
E)8

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
65
Determine the convergence or divergence of the following series. Use a symbolic algebra utility to verify your result.
A)The series diverges.
B)The series converges.
A)The series diverges.
B)The series converges.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
66
Determine whether the series is a p-series.
A) is not a series.
B) is a series.
A) is not a series.
B) is a series.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
67
What are the next three terms in the arithmetic sequence ?
A)
B)
C)
D)
E)
A)

B)
C)
D)

E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
68
Determine the convergence or divergence of the series . Use a symbolic algebra utility to verify your result.
A)The series converges.
B)The series diverges.
A)The series converges.
B)The series diverges.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
69
Determine the convergence or divergence of the series . Use a symbolic algebra utility to verify your result.
A)The series converges.
B)The series diverges.
A)The series converges.
B)The series diverges.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
70
Find the next three terms of the geometric sequence.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
71
Express the value of the given repeating decimal as a fraction. [Hint: Write as an infinite series.]
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
72
Write the first five terms of the sequence of partial sums.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
73
The annual spending by tourists in a resort city is 200 million dollars. Approximately 75% of that revenue is again spent in the resort city, and of that amount approximately 75% is again spent in the resort city. If this pattern continues, write the geometric series that gives the total amount of spending generated by the 200 million dollars (including the initial outlay of 200 million dollars) and find the sum of the series.
A)The geometric series is .The sum of the series is 800.00 million.
B)The geometric series is .The sum of the series is 15,000 million.
C)The geometric series is .The sum of the series is 800.00 million.
D)The geometric series is .The sum of the series is 15,000 million.
E)The geometric series is .The sum of the series is 150.00 million.
A)The geometric series is .The sum of the series is 800.00 million.
B)The geometric series is .The sum of the series is 15,000 million.
C)The geometric series is .The sum of the series is 800.00 million.
D)The geometric series is .The sum of the series is 15,000 million.
E)The geometric series is .The sum of the series is 150.00 million.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
74
You accept a job that pays a salary of 50,000 the first year. During the next 39 years, you will receive a 4% raise each year. What would be your total compensation over the 40-year period? Round your answer to the nearest integer.
A) 4,751,276
B) 1,250,000
C) 48,000
D) 200,000
E) 2,000
A) 4,751,276
B) 1,250,000
C) 48,000
D) 200,000
E) 2,000

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
75
Consider the sequence (An) whose nth term is given by An where P is the principal, An is the amount of compound interest after n months, and r is the annual percentage rate. Write the first four terms of the sequence for P = 8,000 and r = 0.04. Round your answer to two decimal places.
A)8026.67, 8063.49, 8101.43, 8107.20
B)8027.67, 8063.49, 8101.43, 8135.19
C)8026.67, 8053.42, 8080.27, 8107.20
D)8027.67, 8063.49, 8080.27, 8107.20
E)8027.67, 8053.42, 8080.27, 8135.19
A)8026.67, 8063.49, 8101.43, 8107.20
B)8027.67, 8063.49, 8101.43, 8135.19
C)8026.67, 8053.42, 8080.27, 8107.20
D)8027.67, 8063.49, 8080.27, 8107.20
E)8027.67, 8053.42, 8080.27, 8135.19

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
76
A factory is polluting a river such that at every mile down river from the factory an environmental expert finds 20% less pollutant than at the preceding mile. If the pollutant's concentration is 700 ppm (parts per million) at the factory, what is its concentration 15 miles down river?
A)140.00 ppm
B)300.00 ppm
C)24.63 ppm
D)875.00 ppm
E)30.79 ppm
A)140.00 ppm
B)300.00 ppm
C)24.63 ppm
D)875.00 ppm
E)30.79 ppm

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
77
Find the sum of the convergent series.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
78
A company produces a new product for which it estimates the annual sales to be 5000 units. Suppose that in any given year % of the units (regardless of age) will become inoperative. How many units will be in use after n years?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
79
Give an example of a sequence that converges to .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
80
Bouncing Ball. A ball dropped from a height of 35 feet bounces to of its former height with each bounce. Find the total vertical distance that the ball travels.
A)105 feet
B)140 feet
C)64 feet
D)53 feet
E)70 feet
A)105 feet
B)140 feet
C)64 feet
D)53 feet
E)70 feet

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck



