Deck 8: Locus and Concurrence
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/51
Play
Full screen (f)
Deck 8: Locus and Concurrence
1
For 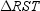 ,
, 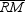 ,
, 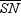 , and
, and 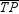 are medians. If TP = 23.4 cm, find the distance between the centroid of
are medians. If TP = 23.4 cm, find the distance between the centroid of 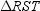 and vertex T .
and vertex T .
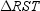 ,
, 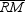 ,
, 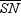 , and
, and 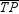 are medians. If TP = 23.4 cm, find the distance between the centroid of
are medians. If TP = 23.4 cm, find the distance between the centroid of 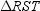 and vertex T .
and vertex T .NOT ANSWERED.
2
How many different lines can be concurrent at point X?
NOT ANSWERED.
3
Where M , N , and P are the midpoints of the sides of 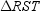 and C is the centroid of the triangle, it follows that
and C is the centroid of the triangle, it follows that 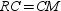 .
.
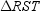 and C is the centroid of the triangle, it follows that
and C is the centroid of the triangle, it follows that 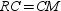 .
.True
4
A number of lines are concurrent if they have exactly one point in common.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
5
To construct the square ABCD with the diagonal 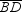 as shown, begin by constructing the perpendicular-bisector of
as shown, begin by constructing the perpendicular-bisector of  .
.
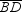 as shown, begin by constructing the perpendicular-bisector of
as shown, begin by constructing the perpendicular-bisector of  .
.
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
6
In 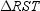 , the medians are
, the medians are 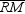 ,
, 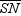 , and
, and 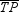 . If RM = 9, SN = 12, and TP = 16, find the distance from the centroid of this triangle to the midpoint of side
. If RM = 9, SN = 12, and TP = 16, find the distance from the centroid of this triangle to the midpoint of side 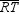 .
.
A)4
B)6
C)8
D)10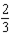
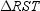 , the medians are
, the medians are 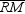 ,
, 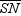 , and
, and 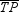 . If RM = 9, SN = 12, and TP = 16, find the distance from the centroid of this triangle to the midpoint of side
. If RM = 9, SN = 12, and TP = 16, find the distance from the centroid of this triangle to the midpoint of side 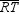 .
.A)4
B)6
C)8
D)10

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
7
In 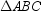 , m
, m 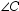 = 90 ° . If AC = 6 and BC = 8, find the distance from vertex C to the midpoint of hypotenuse
= 90 ° . If AC = 6 and BC = 8, find the distance from vertex C to the midpoint of hypotenuse 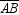 .
.
A)3
B)4
C)5
D)5.6
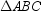 , m
, m 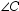 = 90 ° . If AC = 6 and BC = 8, find the distance from vertex C to the midpoint of hypotenuse
= 90 ° . If AC = 6 and BC = 8, find the distance from vertex C to the midpoint of hypotenuse 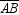 .
.A)3
B)4
C)5
D)5.6

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
8
If m 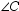 = 90 ° in right triangle
= 90 ° in right triangle  , then
, then 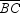 is an altitude of that triangle.
is an altitude of that triangle.
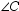 = 90 ° in right triangle
= 90 ° in right triangle  , then
, then 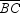 is an altitude of that triangle.
is an altitude of that triangle.
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
9
In 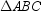 , AB = BC = 17 and AC = 16. Find the distance from the centroid of
, AB = BC = 17 and AC = 16. Find the distance from the centroid of 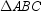 to side
to side 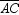 .
.
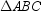 , AB = BC = 17 and AC = 16. Find the distance from the centroid of
, AB = BC = 17 and AC = 16. Find the distance from the centroid of 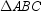 to side
to side 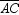 .
.
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
10
In 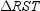 ,
, 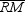 ,
, 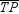 , and
, and 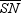 are medians. If the centroid of the triangle is point C , find the relationship between TC and PC .
are medians. If the centroid of the triangle is point C , find the relationship between TC and PC .
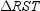 ,
, 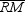 ,
, 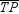 , and
, and 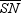 are medians. If the centroid of the triangle is point C , find the relationship between TC and PC .
are medians. If the centroid of the triangle is point C , find the relationship between TC and PC .
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
11
Which of the following lines (line segments)are concurrent?
A)angle-bisectors of a rectangle
B)perpendicular-bisectors of the sides of a rhombus
C)angle-bisectors of a trapezoid
D)angle-bisectors of a kite
A)angle-bisectors of a rectangle
B)perpendicular-bisectors of the sides of a rhombus
C)angle-bisectors of a trapezoid
D)angle-bisectors of a kite

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
12
To locate the circumcenter of a triangle, one must construct or draw all three perpendicular-bisectors of the sides of that triangle.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
13
The point at which the three angle-bisectors of the angles of a triangle are concurrent is known as the circumcenter of the triangle.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
14
To construct an isosceles triangle with vertex angle 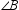 and legs of length RS :
and legs of length RS :
A)construct another angle congruent to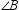
B)mark off an arc from B of length RS on side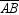
C)mark off an arc from B of length RS to intersect both sides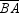 and
and 
D)None of These
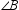 and legs of length RS :
and legs of length RS :A)construct another angle congruent to
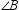
B)mark off an arc from B of length RS on side
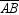
C)mark off an arc from B of length RS to intersect both sides
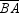 and
and 
D)None of These

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
15
For what type of triangle are the angle-bisectors, perpendicular-bisectors of sides, altitudes, and medians the same?

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
16
The three altitudes of an obtuse triangle are concurrent at a point that lies in the exterior of that triangle.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
17
If lines l, m, and n are concurrent, then:
A)they intersect at one point
B)they are parallel
C)they do not determine a plane
D)None of These
A)they intersect at one point
B)they are parallel
C)they do not determine a plane
D)None of These

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
18
In 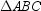 , angle-bisectors
, angle-bisectors 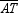 ,
, 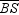 , and
, and 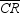 are concurrent at point X . If m
are concurrent at point X . If m 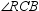 = 27 ° and m
= 27 ° and m 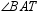 = 32 ° , find m
= 32 ° , find m  .
.
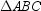 , angle-bisectors
, angle-bisectors 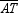 ,
, 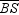 , and
, and 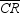 are concurrent at point X . If m
are concurrent at point X . If m 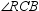 = 27 ° and m
= 27 ° and m 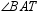 = 32 ° , find m
= 32 ° , find m  .
.
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
19
For equilateral triangle 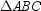 with center O ,
with center O ,  (if drawn)would be an apothem.
(if drawn)would be an apothem.
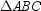 with center O ,
with center O ,  (if drawn)would be an apothem.
(if drawn)would be an apothem.
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
20
To construct the altitude from vertex A to side 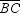 of the obtuse triangle
of the obtuse triangle 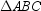 , one begins by constructing the midpoint of
, one begins by constructing the midpoint of  .
.
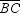 of the obtuse triangle
of the obtuse triangle 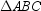 , one begins by constructing the midpoint of
, one begins by constructing the midpoint of  .
.
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
21
In regular hexagon ABCDEF , diagonals 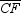 and
and 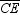 are drawn. Find m
are drawn. Find m 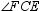 .
.
A)30 °
B)45 °
C)60 °
D)None of These
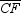 and
and 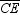 are drawn. Find m
are drawn. Find m 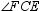 .
.A)30 °
B)45 °
C)60 °
D)None of These

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
22
In regular hexagon ABCDEF , AB = 12. Find the length of diagonal 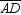 .
.
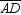 .
.
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
23
Find the length of a side for a regular hexagon whose apothem has length 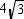 cm.
cm.
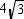 cm.
cm.
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
24
If the length of each apothem of a square is a, then the length of each side is 2a.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
25
For 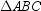 , what is the name of the circle that has its center O determined by the three perpendicular-bisectors of the sides of the triangle and radius of length OA ?
, what is the name of the circle that has its center O determined by the three perpendicular-bisectors of the sides of the triangle and radius of length OA ?
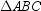 , what is the name of the circle that has its center O determined by the three perpendicular-bisectors of the sides of the triangle and radius of length OA ?
, what is the name of the circle that has its center O determined by the three perpendicular-bisectors of the sides of the triangle and radius of length OA ?
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
26
For what type of regular polygon does the apothem have a length equal to one-half the length of a side of the polygon?

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
27
Determine the number of sides in a regular polygon whose central angles each measure 24°.
A)10
B)12
C)14
D)15
A)10
B)12
C)14
D)15

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
28
For the regular pentagon shown, find the measure of a central angle.
A)36 °
B)72 °
C)108 °
D)None of These
A)36 °
B)72 °
C)108 °
D)None of These

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
29
In isosceles triangle 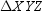 , XY = YZ = 10, and XZ = 16. Where C is the centroid of
, XY = YZ = 10, and XZ = 16. Where C is the centroid of 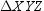 , find the distance from C to side
, find the distance from C to side 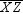 of the triangle.
of the triangle.
A)2
B)2.5
C)3
D)4
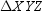 , XY = YZ = 10, and XZ = 16. Where C is the centroid of
, XY = YZ = 10, and XZ = 16. Where C is the centroid of 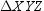 , find the distance from C to side
, find the distance from C to side 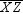 of the triangle.
of the triangle.A)2
B)2.5
C)3
D)4

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
30
For any regular polygon, the center can be determined by the intersection of any two angle-bisectors of the polygon.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
31
Consider the triangle with sides of lengths a, b, and c. How would you construct a larger triangle similar to the first triangle but with a constant of proportionality of 2?

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
32
For a regular pentagon, the measure of each central angle is 72°.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
33
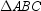 is an equilateral triangle with center O . If the distance from O to each vertex is 6 cm, how long is each side of
is an equilateral triangle with center O . If the distance from O to each vertex is 6 cm, how long is each side of 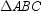 ?
?A)3 cm
B)
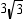 cm
cmC)6 cm
D)
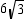 cm
cm
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
34
Find the number of sides for a regular polygon in which each interior angle is 120° larger than each exterior angle.
A)9
B)12
C)15
D)18
A)9
B)12
C)15
D)18

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
35
In regular decagon QRSTUVWXYZ , 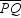 is a radius. Find m
is a radius. Find m 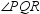 .
.
A)45 °
B)60 °
C)72 °
D)144 °
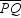 is a radius. Find m
is a radius. Find m 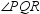 .
.A)45 °
B)60 °
C)72 °
D)144 °

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
36
In order to circumscribe a circle about regular hexagon ABCDEF, we bisect angle A and B to determine center O as the intersection. What is the radius length for the circle?

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
37
A circle can be inscribed within or circumscribed about any regular polygon.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
38
For 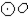 , points A , B , C , D , and E are equally spaced on the circle in that order. If tangents are constructed at these points, what type of polygon circumscribes this circle?
, points A , B , C , D , and E are equally spaced on the circle in that order. If tangents are constructed at these points, what type of polygon circumscribes this circle?
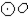 , points A , B , C , D , and E are equally spaced on the circle in that order. If tangents are constructed at these points, what type of polygon circumscribes this circle?
, points A , B , C , D , and E are equally spaced on the circle in that order. If tangents are constructed at these points, what type of polygon circumscribes this circle?
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
39
In regular hexagon ABCDEF ,  is the apothem to side
is the apothem to side 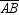 . If CD = 12, find OM
. If CD = 12, find OM
A)6
B)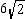
C)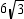
D)None of THese
 is the apothem to side
is the apothem to side 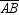 . If CD = 12, find OM
. If CD = 12, find OMA)6
B)
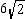
C)
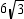
D)None of THese

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
40
In regular octagon ABCDEFGH, AB = 6. Find the perimeter of trapezoid ABCH.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
41
In a regular polygon, each central angle measures 15°. How many sides does the polygon have?

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
42
How is the apothem of a regular polygon related to the side of the polygon to which it is drawn?

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
43
Write the formula for the measure c of the central angle of a regular polygon of n sides.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
44
In an equilateral triangle whose radius has length 6, find the length of an apothem.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
45
To circumscribe a circle about regular hexagon ABCDEF , the center can be determined by the intersection of diagonals 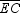 and
and 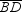 .
.
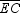 and
and 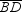 .
.
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
46
In a regular polygon with center O and a side 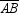 , m
, m 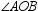 = 72 ° . If AB = 4.6 inches, find the perimeter of the regular polygon.
= 72 ° . If AB = 4.6 inches, find the perimeter of the regular polygon.
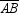 , m
, m 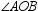 = 72 ° . If AB = 4.6 inches, find the perimeter of the regular polygon.
= 72 ° . If AB = 4.6 inches, find the perimeter of the regular polygon.
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
47
For an equilateral triangle, the incenter and circumcenter are the same point.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
48
For a square ABCD , the length of radius is 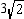 cm. Find the perimeter of ABCD .
cm. Find the perimeter of ABCD .
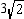 cm. Find the perimeter of ABCD .
cm. Find the perimeter of ABCD .
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
49
How is the radius of a regular polygon related to the angle to whose vertex the radius was drawn?

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
50
To inscribe a circle in a square, the center can be found by the intersection of the two diagonals.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
51
In a regular pentagon, each side has the length 4.8 inches while the apothem has the length 7.4 inches. To the nearest tenth of an inch, find the length of the radius of the pentagon.

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck



