Deck 12: Elections and Electoral Systems
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/52
Play
Full screen (f)
Deck 12: Elections and Electoral Systems
1
About half of the legislative and presidential elections that took place between 1946 and 2000 were held in dictatorships.
True
2
Some scholars argue that elections in dictatorships serve a purpose even if they are not the mechanism for selecting leaders. They argue that elections can stabilize the dictatorship by:
A) discouraging opposition groups from challenging the dictator.
B) dividing the opposition by allowing some groups to participate but not others.
C) presenting a democratic "appearance" to satisfy international organizations.
D) all of these are reasons given to explain why dictatorships have elections.
A) discouraging opposition groups from challenging the dictator.
B) dividing the opposition by allowing some groups to participate but not others.
C) presenting a democratic "appearance" to satisfy international organizations.
D) all of these are reasons given to explain why dictatorships have elections.
D
3
What is (are) the key difference(s) between majoritarian and proportional representation (PR) electoral systems?
A) In majoritarian systems, the winning candidate(s) must win a majority or plurality of the vote, whereas this is not necessary in PR systems.
B) PR systems use large district magnitudes or two-round systems in single districts to elect candidates.
C) All PR systems use party lists.
D) All of these are differences between majoritarian and PR systems.
A) In majoritarian systems, the winning candidate(s) must win a majority or plurality of the vote, whereas this is not necessary in PR systems.
B) PR systems use large district magnitudes or two-round systems in single districts to elect candidates.
C) All PR systems use party lists.
D) All of these are differences between majoritarian and PR systems.
A
4
What is the district magnitude in a single-member district?
A) 1
B) 2
C) 10
D) Can't say based on the information given
A) 1
B) 2
C) 10
D) Can't say based on the information given

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
5
Is it possible for a candidate to win in a majoritarian electoral system, such as single-member district plurality, without receiving a majority of the votes?

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
6
Single-member district plurality (SMDP) systems are sometimes criticized because they:
A) do not allow voters to hold their representatives accountable very easily.
B) can produce very unrepresentative electoral outcomes at the district level.
C) both (A) and (B) are common criticisms of SMDP systems.
A) do not allow voters to hold their representatives accountable very easily.
B) can produce very unrepresentative electoral outcomes at the district level.
C) both (A) and (B) are common criticisms of SMDP systems.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
7
Imagine that you lived in the constituency of St. Ives in the United Kingdom and that your preference ordering among the political parties was Labour > Liberal > Liberal Democrat > Conservative. The electoral system is a single-member district plurality system. Look at Table 1 and answer the following questions.
-If you were to vote sincerely, which party's candidate would you vote for?
A) Conservative
B) Liberal Democrat
C) Labour
D) Liberal
-If you were to vote sincerely, which party's candidate would you vote for?
A) Conservative
B) Liberal Democrat
C) Labour
D) Liberal

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
8
Imagine that you lived in the constituency of St. Ives in the United Kingdom and that your preference ordering among the political parties was Labour > Liberal > Liberal Democrat > Conservative. The electoral system is a single-member district plurality system. Look at Table 1 and answer the following questions.
-If you were to vote strategically, which party's candidate would you vote for?
A) Conservative
B) Liberal Democrat
C) Labour
D) Liberal
-If you were to vote strategically, which party's candidate would you vote for?
A) Conservative
B) Liberal Democrat
C) Labour
D) Liberal

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
9
The most common method used for electing presidents in the world today is the majority-runoff two-round system.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
10
The supplementary vote system is cheaper for election officials to administer than majority runoff two-round systems are.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
11
We can characterize all proportional representation systems as those with multimember districts and in which either a quota or a divisor is used to determine which candidates are elected in a district.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
12
The hypothetical election results shown in Table 2 correspond to question.
-The election results in Table 2 are for a district in which 10 candidates are elected. This country uses the Hare quota with largest remainders to allocate seats. If the Hare quota is calculated as the total number of votes in the district divided by the total number of seats available in the district, what is the Hare quota in this district?
A) 35,000
B) 10,000
C) 3,000
D) 100,000
E) not enough information provided to calculate the Hare quota
-The election results in Table 2 are for a district in which 10 candidates are elected. This country uses the Hare quota with largest remainders to allocate seats. If the Hare quota is calculated as the total number of votes in the district divided by the total number of seats available in the district, what is the Hare quota in this district?
A) 35,000
B) 10,000
C) 3,000
D) 100,000
E) not enough information provided to calculate the Hare quota

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
13
The hypothetical election results shown in Table 2 correspond to question.
-In the district described in Table 2, how many total seats does Party B win?
A) 0
B) 1
C) 2
D) 3
E) 4
F) 5
-In the district described in Table 2, how many total seats does Party B win?
A) 0
B) 1
C) 2
D) 3
E) 4
F) 5

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
14
The hypothetical election results shown in Table 2 correspond to question.
-In the district described in Table 2, how many total seats does Party E win?
A) 0
B) 1
C) 2
D) 3
E) 4
F) 5
-In the district described in Table 2, how many total seats does Party E win?
A) 0
B) 1
C) 2
D) 3
E) 4
F) 5

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
15
Now imagine that the votes for each party shown in Table 2 are the same, but that they are for a district where 10 candidates are elected using a highest average system to allocate seats. This means that the votes parties receive are divided by a series of numbers to give quotients. This country uses the d'Hondt method (the divisors are 1, 2, 3, 4, . . . ). Seats are allocated to the party with the largest quotient, then the second largest, then the third largest . . . until all of the seats have been allocated. In Table 3, the quotients have already been calculated for you and are shown in italics. Use Table 3 to answer Questions .
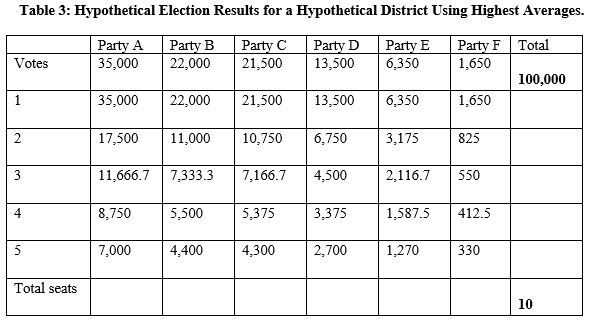
-In the district described in Table 3, how many total seats does Party B win?
A) 0
B) 1
C) 2
D) 3
E) 4
F) 5

-In the district described in Table 3, how many total seats does Party B win?
A) 0
B) 1
C) 2
D) 3
E) 4
F) 5

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
16
Now imagine that the votes for each party shown in Table 2 are the same, but that they are for a district where 10 candidates are elected using a highest average system to allocate seats. This means that the votes parties receive are divided by a series of numbers to give quotients. This country uses the d'Hondt method (the divisors are 1, 2, 3, 4, . . . ). Seats are allocated to the party with the largest quotient, then the second largest, then the third largest . . . until all of the seats have been allocated. In Table 3, the quotients have already been calculated for you and are shown in italics. Use Table 3 to answer Questions .

-In the district described in Table 3, how many total seats does Party E win?
A) 0
B) 1
C) 2
D) 3
E) 4
F) 5

-In the district described in Table 3, how many total seats does Party E win?
A) 0
B) 1
C) 2
D) 3
E) 4
F) 5

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
17
Now imagine that the votes for each party shown in Table 2 are the same, but that they are for a district where 10 candidates are elected using a highest average system to allocate seats. This means that the votes parties receive are divided by a series of numbers to give quotients. This country uses the d'Hondt method (the divisors are 1, 2, 3, 4, . . . ). Seats are allocated to the party with the largest quotient, then the second largest, then the third largest . . . until all of the seats have been allocated. In Table 3, the quotients have already been calculated for you and are shown in italics. Use Table 3 to answer Questions .

-If the election results shown in Table 3 above were for a district with a magnitude of 1 and plurality rule was used (in other words, you have an single-member district plurality system), what would the outcome be?
A) Candidates from parties A and B would each win 5 seats.
B) Candidates from party A would win 10 seats.
C) A candidate from party A would win 1 seat and the other parties would get 0 seats.
D) You can't answer this question unless you know what the second, third, fourth, and so on, preference ranking is on each ballot that was cast.

-If the election results shown in Table 3 above were for a district with a magnitude of 1 and plurality rule was used (in other words, you have an single-member district plurality system), what would the outcome be?
A) Candidates from parties A and B would each win 5 seats.
B) Candidates from party A would win 10 seats.
C) A candidate from party A would win 1 seat and the other parties would get 0 seats.
D) You can't answer this question unless you know what the second, third, fourth, and so on, preference ranking is on each ballot that was cast.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
18
Now imagine that the votes for each party shown in Table 2 are the same, but that they are for a district where 10 candidates are elected using a highest average system to allocate seats. This means that the votes parties receive are divided by a series of numbers to give quotients. This country uses the d'Hondt method (the divisors are 1, 2, 3, 4, . . . ). Seats are allocated to the party with the largest quotient, then the second largest, then the third largest . . . until all of the seats have been allocated. In Table 3, the quotients have already been calculated for you and are shown in italics. Use Table 3 to answer Questions .

-If the election results shown in Table 3, above, were for a district with a magnitude of 1 and the alternative vote rule was used, what would the outcome be?
A) candidates from parties A and B would each win 5 seats.
B) candidates from party A would win 10 seats.
C) a candidate from party A would win 1 seat and the other parties would get 0 seats.
D) you can't answer this question unless you know what the second, third, fourth, and so on, preference ranking is on each ballot that was cast.

-If the election results shown in Table 3, above, were for a district with a magnitude of 1 and the alternative vote rule was used, what would the outcome be?
A) candidates from parties A and B would each win 5 seats.
B) candidates from party A would win 10 seats.
C) a candidate from party A would win 1 seat and the other parties would get 0 seats.
D) you can't answer this question unless you know what the second, third, fourth, and so on, preference ranking is on each ballot that was cast.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
19
All proportional electoral systems have natural thresholds. Some have formal thresholds written into the electoral law as well.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
20
Which type of party list gives the most power to the party leadership (over the individual candidates)?
A) closed party list
B) open party list
C) free party list
A) closed party list
B) open party list
C) free party list

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
21
Countries with electoral tiers above the district level are typically more favorable to smaller parties.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
22
Which of the following is NOT a disadvantage of the single nontransferable vote system?
A) few incentives to build broad-based coalitions
B) encourages patronage
C) strengthens parties
D) favors well-organized parties
A) few incentives to build broad-based coalitions
B) encourages patronage
C) strengthens parties
D) favors well-organized parties

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
23
What is a mixed electoral system?
A) It is when the government depends on the legislature and the president.
B) It is when you have districts that elect different numbers of people.
C) It is when the electoral system uses both a majoritarian formula and a proportional formula.
D) It is when you have multimember districts.
E) It is when the winning candidate must win a majority or plurality of the vote.
A) It is when the government depends on the legislature and the president.
B) It is when you have districts that elect different numbers of people.
C) It is when the electoral system uses both a majoritarian formula and a proportional formula.
D) It is when you have multimember districts.
E) It is when the winning candidate must win a majority or plurality of the vote.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
24
The electoral system used by the most countries is:
A) single-member district plurality.
B) two-round systems.
C) list PR.
D) single nontransferable vote.
A) single-member district plurality.
B) two-round systems.
C) list PR.
D) single nontransferable vote.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
25
Most people in the world live under which type of electoral system?
A) single-member district plurality
B) two-round systems
C) list PR
D) single nontransferable vote
A) single-member district plurality
B) two-round systems
C) list PR
D) single nontransferable vote

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
26
Most dictatorships (measured by the Freedom House measure) that hold elections use which type of electoral rules?
A) majoritarian
B) proportional
C) mixed
A) majoritarian
B) proportional
C) mixed

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
27
The choice of electoral systems in former colonies across the world was strongly influenced by the electoral system used by the former colonial ruler. Thus, many former British colonies use single-member district plurality, whereas many former French colonies use two-round system.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
28
The electoral system used for legislative elections (for the House of Representatives) in the United States is:
A) single-member district plurality.
B) two-round system.
C) list PR.
D) single nontransferable vote.
A) single-member district plurality.
B) two-round system.
C) list PR.
D) single nontransferable vote.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
29
What is measured by "district magnitude"?
A) the number of voters in a district
B) the geographic size of the district
C) the number of seats in a district
D) the relative importance of the district
A) the number of voters in a district
B) the geographic size of the district
C) the number of seats in a district
D) the relative importance of the district

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
30
Use the information in Table 4, below, for the following questions.
-Imagine that the election results in Table 4 are for a country using single-member district plurality rule to elect its candidates. Which party or parties will win in this district?
A) Party A
B) Party B
C) Party C
D) Party D
E) Party E
-Imagine that the election results in Table 4 are for a country using single-member district plurality rule to elect its candidates. Which party or parties will win in this district?
A) Party A
B) Party B
C) Party C
D) Party D
E) Party E

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
31
Use the information in Table 4, below, for the following questions.
-Imagine now that the election results in Table 4 are the first preference votes in a majoritarian system that uses an alternative voting rule (like Australia) where a candidate is automatically elected if he wins an absolute majority of first-round preferences. Which party's candidate wins the single available seat in this district?
A) The candidate from Party A.
B) The candidate from Party B.
C) Both the candidate from Party A and the candidate from Party B will win seats.
D) It will depend on the preference rankings for each candidate, so it is impossible to answer this question based on the information provided.
-Imagine now that the election results in Table 4 are the first preference votes in a majoritarian system that uses an alternative voting rule (like Australia) where a candidate is automatically elected if he wins an absolute majority of first-round preferences. Which party's candidate wins the single available seat in this district?
A) The candidate from Party A.
B) The candidate from Party B.
C) Both the candidate from Party A and the candidate from Party B will win seats.
D) It will depend on the preference rankings for each candidate, so it is impossible to answer this question based on the information provided.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
32
Imagine now that these election results are for a district where ten candidates are elected. This country uses the Hare quota with largest remainders to allocate seats. To answer the following questions, you may want to use Table 5, below.
-If the Hare quota is calculated as the Total Number of Votes in the district divided by the total number of seats available, what is the Hare quota in the hypothetical district in Table 5?
A) 47,000
B) 10,000
C) 1,000
D) 100,000
-If the Hare quota is calculated as the Total Number of Votes in the district divided by the total number of seats available, what is the Hare quota in the hypothetical district in Table 5?
A) 47,000
B) 10,000
C) 1,000
D) 100,000

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
33
Imagine now that these election results are for a district where ten candidates are elected. This country uses the Hare quota with largest remainders to allocate seats. To answer the following questions, you may want to use Table 5, below.
-How many remainder seats does Party A win?
A) 1
B) 2
C) 3
D) 4
E) 5
-How many remainder seats does Party A win?
A) 1
B) 2
C) 3
D) 4
E) 5

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
34
Imagine now that these election results are for a district where ten candidates are elected. This country uses the Hare quota with largest remainders to allocate seats. To answer the following questions, you may want to use Table 5, below.
-How many total seats does Party A win?
A) 1
B) 2
C) 3
D) 4
E) 5
-How many total seats does Party A win?
A) 1
B) 2
C) 3
D) 4
E) 5

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
35
Imagine now that these election results are for a district where ten candidates are elected. This country uses the Hare quota with largest remainders to allocate seats. To answer the following questions, you may want to use Table 5, below.
-How many automatic seats does Party D win?
A) 1
B) 2
C) 3
D) 4
E) 5
-How many automatic seats does Party D win?
A) 1
B) 2
C) 3
D) 4
E) 5

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
36
Imagine now that these election results are for a district where ten candidates are elected. This country uses the Hare quota with largest remainders to allocate seats. To answer the following questions, you may want to use Table 5, below.
-How many total seats does Party E win?
A) 0
B) 1
C) 2
D) 3
E) 4
-How many total seats does Party E win?
A) 0
B) 1
C) 2
D) 3
E) 4

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
37
Imagine now that these election results are for a district where ten candidates are elected. This country uses the Hare quota with largest remainders to allocate seats. To answer the following questions, you may want to use Table 5, below.
-How many total seats does Party F win?
A) 0
B) 1
C) 2
D) 3
E) 4
-How many total seats does Party F win?
A) 0
B) 1
C) 2
D) 3
E) 4

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
38
Electoral systems with upper tiers (electoral tiers above the district level) are typically more favorable to smaller parties than electoral systems with a single tier.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
39
Is party discipline normally higher when open party lists are used or when closed party lists are used in proportional representation systems?
A) open party lists
B) closed party lists
C) it's about the same
A) open party lists
B) closed party lists
C) it's about the same

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
40
A common side effect of electoral thresholds is that voters for small parties end up wasting their votes if the party they voted for cannot surpass the threshold. This is more likely to occur when the threshold is high.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
41
Answer the following questions.
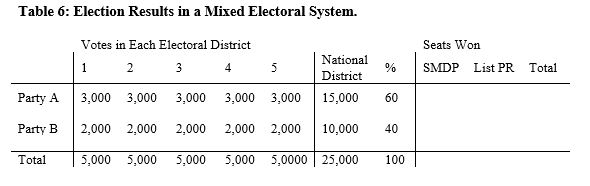
-If the
SMDP = single-member district plurality
If mixed system were "independent," how many SMDP seats would Party A win?
A) 0
B) 2
C) 3
D) 4
E) 5

-If the
SMDP = single-member district plurality
If mixed system were "independent," how many SMDP seats would Party A win?
A) 0
B) 2
C) 3
D) 4
E) 5

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
42
Answer the following questions.

-If the mixed system were "independent," how many TOTAL seats would Party A win?
A) 4
B) 5
C) 6
D) 7
E) 8

-If the mixed system were "independent," how many TOTAL seats would Party A win?
A) 4
B) 5
C) 6
D) 7
E) 8

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
43
Answer the following questions.

-If the mixed system were "dependent," how many single-member district plurality seats would Party A win?
A) 0
B) 2
C) 3
D) 4
E) 5

-If the mixed system were "dependent," how many single-member district plurality seats would Party A win?
A) 0
B) 2
C) 3
D) 4
E) 5

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
44
Answer the following questions.

-If the mixed system were "dependent," how many TOTAL seats would Party A win?
A) 4
B) 5
C) 6
D) 7
E) 8

-If the mixed system were "dependent," how many TOTAL seats would Party A win?
A) 4
B) 5
C) 6
D) 7
E) 8

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
45
All electoral systems create at least some incentive for actors to behave strategically rather than reveal their sincere preferences.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
46
Choosing Electoral Rules: A Game-Theoretic Approach
When would incumbent politicians be likely to abandon disproportional single-member district electoral laws in favor of a "fairer" proportional representation system (as occurred in New Zealand about a decade ago)?
The following game can be used to explain the prospects for institutional reform in democracies. To keep things simple, we can think about the prospect for institutional reform (such as a change from single-member district plurality rule to proportional representation) as a game between a large party and a small party. They each must decide whether to vote for or against the proposed electoral reform. If the large party votes against reform, reform efforts fail and the next election is conducted under the existing rules.
Assume that voters prefer a more proportional electoral system. Thus, parties enjoy an electoral benefit if they vote for reform, but only if the other party votes against reform. Conversely, if a party votes against the reform, it pays a cost, but only if the other party votes for. Payoffs representing this electoral reform game are displayed in the following strategic-form game, where the large party's net electoral benefits from blocking reform are larger than the benefits the parties enjoy from being seen as lone reformers.
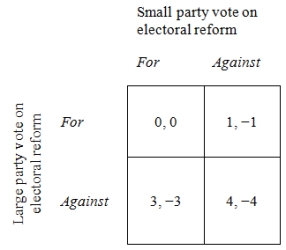
Figure 1. The Electoral Reform Game-Example 1
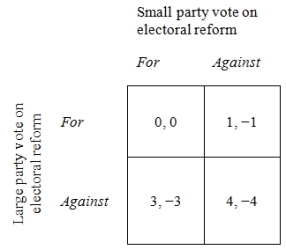
-What strategy combination(s) form(s) a Nash equilibrium in the above game? Hint: use the form (Large strategy; Small strategy).
A) For; For
B) For; Against and Against; For
C) Against; For
D) Against; Against
E) For; Against
When would incumbent politicians be likely to abandon disproportional single-member district electoral laws in favor of a "fairer" proportional representation system (as occurred in New Zealand about a decade ago)?
The following game can be used to explain the prospects for institutional reform in democracies. To keep things simple, we can think about the prospect for institutional reform (such as a change from single-member district plurality rule to proportional representation) as a game between a large party and a small party. They each must decide whether to vote for or against the proposed electoral reform. If the large party votes against reform, reform efforts fail and the next election is conducted under the existing rules.
Assume that voters prefer a more proportional electoral system. Thus, parties enjoy an electoral benefit if they vote for reform, but only if the other party votes against reform. Conversely, if a party votes against the reform, it pays a cost, but only if the other party votes for. Payoffs representing this electoral reform game are displayed in the following strategic-form game, where the large party's net electoral benefits from blocking reform are larger than the benefits the parties enjoy from being seen as lone reformers.
Figure 1. The Electoral Reform Game-Example 1

-What strategy combination(s) form(s) a Nash equilibrium in the above game? Hint: use the form (Large strategy; Small strategy).
A) For; For
B) For; Against and Against; For
C) Against; For
D) Against; Against
E) For; Against

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
47
Choosing Electoral Rules: A Game-Theoretic Approach
When would incumbent politicians be likely to abandon disproportional single-member district electoral laws in favor of a "fairer" proportional representation system (as occurred in New Zealand about a decade ago)?
The following game can be used to explain the prospects for institutional reform in democracies. To keep things simple, we can think about the prospect for institutional reform (such as a change from single-member district plurality rule to proportional representation) as a game between a large party and a small party. They each must decide whether to vote for or against the proposed electoral reform. If the large party votes against reform, reform efforts fail and the next election is conducted under the existing rules.
Assume that voters prefer a more proportional electoral system. Thus, parties enjoy an electoral benefit if they vote for reform, but only if the other party votes against reform. Conversely, if a party votes against the reform, it pays a cost, but only if the other party votes for. Payoffs representing this electoral reform game are displayed in the following strategic-form game, where the large party's net electoral benefits from blocking reform are larger than the benefits the parties enjoy from being seen as lone reformers.
Figure 1. The Electoral Reform Game-Example 1

-If this were an accurate model of a particular country at a particular time, what would you predict about the behavior of the parties?
A) Both parties will support reforms.
B) Neither party will support reforms.
C) The large party will support reforms, but the small party will oppose them.
D) The large party will oppose reforms, but the small party will support them.
E) No way to tell based on the information given here.
When would incumbent politicians be likely to abandon disproportional single-member district electoral laws in favor of a "fairer" proportional representation system (as occurred in New Zealand about a decade ago)?
The following game can be used to explain the prospects for institutional reform in democracies. To keep things simple, we can think about the prospect for institutional reform (such as a change from single-member district plurality rule to proportional representation) as a game between a large party and a small party. They each must decide whether to vote for or against the proposed electoral reform. If the large party votes against reform, reform efforts fail and the next election is conducted under the existing rules.
Assume that voters prefer a more proportional electoral system. Thus, parties enjoy an electoral benefit if they vote for reform, but only if the other party votes against reform. Conversely, if a party votes against the reform, it pays a cost, but only if the other party votes for. Payoffs representing this electoral reform game are displayed in the following strategic-form game, where the large party's net electoral benefits from blocking reform are larger than the benefits the parties enjoy from being seen as lone reformers.
Figure 1. The Electoral Reform Game-Example 1

-If this were an accurate model of a particular country at a particular time, what would you predict about the behavior of the parties?
A) Both parties will support reforms.
B) Neither party will support reforms.
C) The large party will support reforms, but the small party will oppose them.
D) The large party will oppose reforms, but the small party will support them.
E) No way to tell based on the information given here.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
48
Now, suppose the large party controls which bills are voted on (perhaps because it controls the relevant committee in the legislature). The game below is similar to the one above, but now the large party can choose to propose a reform (in which case the parties play a version of the game above), or they can block a reform bill before it gets to the floor (in which case they compete against the small party under existing laws). Answer the following questions.
Figure 2: The Electoral Reform Game-When the Large Party Controls the Legislative Agenda
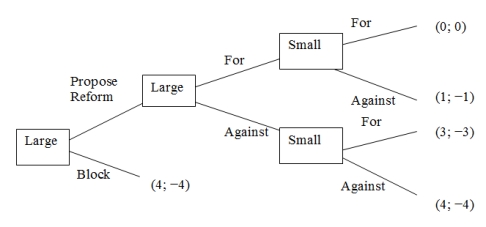
-What strategy combinations form a subgame perfect Nash equilibrium to the above game? Hint: use the form (Large's move at first node, Large's move at second node; Small's move at top node, Small's move at bottom node).
A) Block
B) Block, Against; For, Against
C) Block, Against; For, For
D) Propose reform, For; For, Against
E) Against; For
Figure 2: The Electoral Reform Game-When the Large Party Controls the Legislative Agenda

-What strategy combinations form a subgame perfect Nash equilibrium to the above game? Hint: use the form (Large's move at first node, Large's move at second node; Small's move at top node, Small's move at bottom node).
A) Block
B) Block, Against; For, Against
C) Block, Against; For, For
D) Propose reform, For; For, Against
E) Against; For

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
49
Now, suppose the large party controls which bills are voted on (perhaps because it controls the relevant committee in the legislature). The game below is similar to the one above, but now the large party can choose to propose a reform (in which case the parties play a version of the game above), or they can block a reform bill before it gets to the floor (in which case they compete against the small party under existing laws). Answer the following questions.
Figure 2: The Electoral Reform Game-When the Large Party Controls the Legislative Agenda

-What does your response to the previous question say about the credibility of a large party that (a) controls the proposal process; (b) does not propose reform; but (c) claims that it supports reform?
A) the claim is credible
B) the claim is not credible
Figure 2: The Electoral Reform Game-When the Large Party Controls the Legislative Agenda

-What does your response to the previous question say about the credibility of a large party that (a) controls the proposal process; (b) does not propose reform; but (c) claims that it supports reform?
A) the claim is credible
B) the claim is not credible

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
50
Now, let's ask what happens when the parties play a game like the one in Figure 1,
Figure 1. The Electoral Reform Game-Example 1
 except that the benefit to the large party of having disproportional rules is much less, and the penalties to the smaller party from disproportional electoral rules are lower. This might be because the smaller party has been attracting a larger electorate, whereas the large party has been losing voters. This new situation is modeled in Figure 3 below. Using Figure 3, answer the following questions.
except that the benefit to the large party of having disproportional rules is much less, and the penalties to the smaller party from disproportional electoral rules are lower. This might be because the smaller party has been attracting a larger electorate, whereas the large party has been losing voters. This new situation is modeled in Figure 3 below. Using Figure 3, answer the following questions.
Figure 3. The Electoral Reform Game-Example 2
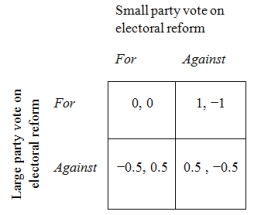
-What strategy combination(s) form(s) a Nash equilibrium in the above game? Hint: use the form (Large strategy; Small strategy).
A) For; For
B) For; Against and Against; For
C) Against; For
D) Against; Against
E) For; Against
Figure 1. The Electoral Reform Game-Example 1
 except that the benefit to the large party of having disproportional rules is much less, and the penalties to the smaller party from disproportional electoral rules are lower. This might be because the smaller party has been attracting a larger electorate, whereas the large party has been losing voters. This new situation is modeled in Figure 3 below. Using Figure 3, answer the following questions.
except that the benefit to the large party of having disproportional rules is much less, and the penalties to the smaller party from disproportional electoral rules are lower. This might be because the smaller party has been attracting a larger electorate, whereas the large party has been losing voters. This new situation is modeled in Figure 3 below. Using Figure 3, answer the following questions.Figure 3. The Electoral Reform Game-Example 2

-What strategy combination(s) form(s) a Nash equilibrium in the above game? Hint: use the form (Large strategy; Small strategy).
A) For; For
B) For; Against and Against; For
C) Against; For
D) Against; Against
E) For; Against

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
51
Now, let's ask what happens when the parties play a game like the one in Figure 1,
Figure 1. The Electoral Reform Game-Example 1
 except that the benefit to the large party of having disproportional rules is much less, and the penalties to the smaller party from disproportional electoral rules are lower. This might be because the smaller party has been attracting a larger electorate, whereas the large party has been losing voters. This new situation is modeled in Figure 3 below. Using Figure 3, answer the following questions.
except that the benefit to the large party of having disproportional rules is much less, and the penalties to the smaller party from disproportional electoral rules are lower. This might be because the smaller party has been attracting a larger electorate, whereas the large party has been losing voters. This new situation is modeled in Figure 3 below. Using Figure 3, answer the following questions.
Figure 3. The Electoral Reform Game-Example 2

-If this were an accurate model of a particular country at a particular time, what would you predict about the behavior of the large party? The small party?
A) Both parties will support reforms.
B) Neither party will support reforms.
C) The large party will support reforms, but the small party will oppose them.
D) The large party will oppose reforms, but the small party will support them.
E) No way to tell.
Figure 1. The Electoral Reform Game-Example 1
 except that the benefit to the large party of having disproportional rules is much less, and the penalties to the smaller party from disproportional electoral rules are lower. This might be because the smaller party has been attracting a larger electorate, whereas the large party has been losing voters. This new situation is modeled in Figure 3 below. Using Figure 3, answer the following questions.
except that the benefit to the large party of having disproportional rules is much less, and the penalties to the smaller party from disproportional electoral rules are lower. This might be because the smaller party has been attracting a larger electorate, whereas the large party has been losing voters. This new situation is modeled in Figure 3 below. Using Figure 3, answer the following questions.Figure 3. The Electoral Reform Game-Example 2

-If this were an accurate model of a particular country at a particular time, what would you predict about the behavior of the large party? The small party?
A) Both parties will support reforms.
B) Neither party will support reforms.
C) The large party will support reforms, but the small party will oppose them.
D) The large party will oppose reforms, but the small party will support them.
E) No way to tell.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
52
Now, let's ask what happens when the parties play a game like the one in Figure 1,
Figure 1. The Electoral Reform Game-Example 1
 except that the benefit to the large party of having disproportional rules is much less, and the penalties to the smaller party from disproportional electoral rules are lower. This might be because the smaller party has been attracting a larger electorate, whereas the large party has been losing voters. This new situation is modeled in Figure 3 below. Using Figure 3, answer the following questions.
except that the benefit to the large party of having disproportional rules is much less, and the penalties to the smaller party from disproportional electoral rules are lower. This might be because the smaller party has been attracting a larger electorate, whereas the large party has been losing voters. This new situation is modeled in Figure 3 below. Using Figure 3, answer the following questions.
Figure 3. The Electoral Reform Game-Example 2

-Compare your answers to the questions that asked you to predict the behavior of the two parties, given the particular game being examined (Questions 46 and 50). What does your analysis of the two games say about the conditions under which politicians who benefit from existing electoral laws are likely to support reforms that will help other parties?
A) Large parties will never support reforms.
B) If a large party is losing its size advantage and there is an electoral advantage from being seen as a reformer, then it will support the reform.
C) Large parties will always support reforms.
D) Can't say based on the information given.
Figure 1. The Electoral Reform Game-Example 1
 except that the benefit to the large party of having disproportional rules is much less, and the penalties to the smaller party from disproportional electoral rules are lower. This might be because the smaller party has been attracting a larger electorate, whereas the large party has been losing voters. This new situation is modeled in Figure 3 below. Using Figure 3, answer the following questions.
except that the benefit to the large party of having disproportional rules is much less, and the penalties to the smaller party from disproportional electoral rules are lower. This might be because the smaller party has been attracting a larger electorate, whereas the large party has been losing voters. This new situation is modeled in Figure 3 below. Using Figure 3, answer the following questions.Figure 3. The Electoral Reform Game-Example 2

-Compare your answers to the questions that asked you to predict the behavior of the two parties, given the particular game being examined (Questions 46 and 50). What does your analysis of the two games say about the conditions under which politicians who benefit from existing electoral laws are likely to support reforms that will help other parties?
A) Large parties will never support reforms.
B) If a large party is losing its size advantage and there is an electoral advantage from being seen as a reformer, then it will support the reform.
C) Large parties will always support reforms.
D) Can't say based on the information given.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck



