Deck 5: Lossy Compression Algorithms, Image Compression Standards and Basic Video Compression Techniques
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/10
Play
Full screen (f)
Deck 5: Lossy Compression Algorithms, Image Compression Standards and Basic Video Compression Techniques
1
Explain why the factorization steps in Eqs. (8.24) and (8.25) save CPU cycles. About how much faster is the factorized approach to the DCT than the straightforward definition in (8.17)? (In both approaches, assume that of course the cosine matrix values are pre-stored outside any loop.)
Not Answer
2
The top part of Figure 8.1 shows the DCT for a 1-D signal .
i. What does tell you in terms of the image content in ?
ii. What is the reason that is less than 0 ?
(b) The Inverse Discrete Cosine Transform (IDCT) can be viewed as a reconstruction process in which the Cosine basis functions are scaled and added one by one to reconstruct . Assume and ; in the space provided at the bottom part of the figure,
i. draw after only the is used,
ii. draw after and are used.
Show all details including magnitudes, and explain why they look like that.
i. What does tell you in terms of the image content in ?
ii. What is the reason that is less than 0 ?
(b) The Inverse Discrete Cosine Transform (IDCT) can be viewed as a reconstruction process in which the Cosine basis functions are scaled and added one by one to reconstruct . Assume and ; in the space provided at the bottom part of the figure,
i. draw after only the is used,
ii. draw after and are used.
Show all details including magnitudes, and explain why they look like that.
Not Answer
3
Suppose we have 32 samples from a mono audio file.
(a) If the audio was sampled at , how many seconds does this represent?
(b) If we carry out a DCT with blocksize equal to 32, how many DCT coefficients do we end up with?
(c) Numbering the DCT coefficients from 0,
i) What frequency, in , does coefficient number 1 represent?
ii) What frequency, in , does coefficient number 16 represent?
(a) If the audio was sampled at , how many seconds does this represent?
(b) If we carry out a DCT with blocksize equal to 32, how many DCT coefficients do we end up with?
(c) Numbering the DCT coefficients from 0,
i) What frequency, in , does coefficient number 1 represent?
ii) What frequency, in , does coefficient number 16 represent?
(a)
(b) 32
(c) i) cycle per 32 samples
cycle per sec
cycles-per-sec cycles-per-sec
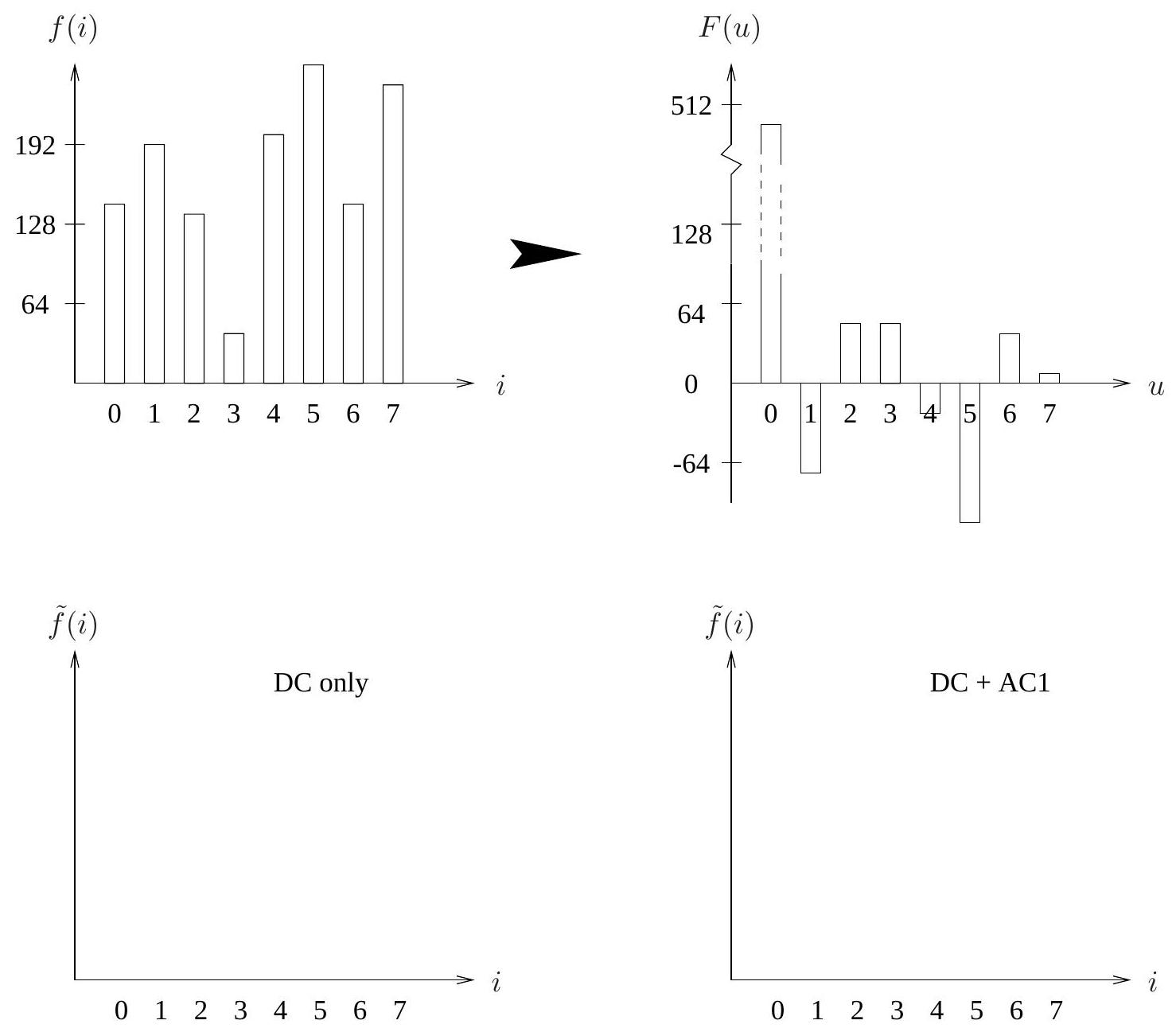 Fig. 8.1: DCT for a 1-D signal; reconstruction using only as opposed to only and .
Fig. 8.1: DCT for a 1-D signal; reconstruction using only as opposed to only and .
ii) cycles per
cycles-per-sec
(Note that the max frequency we analyze for is .)
BEGIN not\_on\_exam:
 END not on exam.
END not on exam.
(b) 32
(c) i) cycle per 32 samples
cycle per sec
cycles-per-sec cycles-per-sec
 Fig. 8.1: DCT for a 1-D signal; reconstruction using only as opposed to only and .
Fig. 8.1: DCT for a 1-D signal; reconstruction using only as opposed to only and .ii) cycles per
cycles-per-sec
(Note that the max frequency we analyze for is .)
BEGIN not\_on\_exam:
 END not on exam.
END not on exam. 4
Another name for zig-zag coding is "zonal coding". Suppose you invent a new zonal coding scheme for JPEG that simply discards diagonals above the first few. Suppose we keep the first six zig-zag lines.
(a) How many coefficients are we keeping?
(b) How will we do, compared to keeping all the zig-zags (still using run-length encoding)? Comment on both compression capability and image quality.
(a) How many coefficients are we keeping?
(b) How will we do, compared to keeping all the zig-zags (still using run-length encoding)? Comment on both compression capability and image quality.

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
5
Briefly explain why DCT was chosen for JPEG compression.

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
6
Why does JPEG give compression? At which points in the algorithm does compression occur? Please estimate (as a general guess) how much compression occurs at each of these points.

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
7
Explain why the block DCT is preferred to taking the whole image DCT in JPEG compression.

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
8
Describe how H.261 deals with temporal and spatial redundancies in video.

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
9
Given the following two consecutive frames in an H.261 video, if the first image is treated as an Iframe and the second a P-frame. Show in detail how the second image is encoded. (Work out the numbers at each step. You can assume any quantizer and stop after the RLC (Run-length Coding).)
To simplify the data, we assume that the size of macroblocks is instead of .
Intensity Values for the First Image:

Intensity Values for the Second Image:

To simplify the data, we assume that the size of macroblocks is instead of .
Intensity Values for the First Image:

Intensity Values for the Second Image:


Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
10
We have seen that a logarithmic-based block search strategy is fast: it is "suboptimal but still usually effective." That being the case, why should we be bothered carrying out a full search in any situation? Why not just stick to the fast method - what is the advantage to be gained, if any, from a comprehensive, optimal search strategy?

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck



