Deck 7: Expected Return and Risk
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/44
Play
Full screen (f)
Deck 7: Expected Return and Risk
1
The calculation of expected value takes into account the:
A) standard deviation of the asset.
B) correlation between a security's risk and return.
C) anticipated future outcomes and their associated probability of occurrence.
D) probabilities from only discrete probability distribution.
A) standard deviation of the asset.
B) correlation between a security's risk and return.
C) anticipated future outcomes and their associated probability of occurrence.
D) probabilities from only discrete probability distribution.
anticipated future outcomes and their associated probability of occurrence.
2
Portfolio weights are found by:
A) using the standard deviation of returns divided by by expected value.
B) calculating the percentage each asset held in relation to the total portfolio value.
C) calculating the return of each asset as a percentage of total portfolio return.
D) using the expected value of returns divided by the standard deviation.
A) using the standard deviation of returns divided by by expected value.
B) calculating the percentage each asset held in relation to the total portfolio value.
C) calculating the return of each asset as a percentage of total portfolio return.
D) using the expected value of returns divided by the standard deviation.
calculating the percentage each asset held in relation to the total portfolio value.
3
Which of the following statements regarding expected return of a portfolio is true?
A) It will be approximately equal to the return on the lowest yielding asset in a portfolio.
B) With correct diversification, it will be higher than the previously highest yielding asset in the portfolio.
C) It is a weighted average expected return of individual assets.
D) Expected return on a portfolio cannot be calculated if the risk-free rate were to change.
A) It will be approximately equal to the return on the lowest yielding asset in a portfolio.
B) With correct diversification, it will be higher than the previously highest yielding asset in the portfolio.
C) It is a weighted average expected return of individual assets.
D) Expected return on a portfolio cannot be calculated if the risk-free rate were to change.
It is a weighted average expected return of individual assets.
4
In order to determine the expected return of a portfolio, all of the following must be known except:
A) probabilities of expected returns of individual assets.
B) weight of each individual asset to total portfolio value.
C) expected return of each individual asset.
D) All of these must be known in order to determine the expected return of a portfolio.
A) probabilities of expected returns of individual assets.
B) weight of each individual asset to total portfolio value.
C) expected return of each individual asset.
D) All of these must be known in order to determine the expected return of a portfolio.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
5
Markowitz diversification is concerned with:
A) risk and return within a portfolio.
B) weighted individual security risks.
C) weighted co-movements between securities' returns.
D) All of the above are encompassed by Markowitz diversification
A) risk and return within a portfolio.
B) weighted individual security risks.
C) weighted co-movements between securities' returns.
D) All of the above are encompassed by Markowitz diversification

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
6
Which of the following statements regarding the correlation coefficient is not true?
A) It is a statistical measure.
B) It measures the relationship between two securities' returns.
C) It determines the causes of the relationship between two securities' returns.
D) All of these are true.
A) It is a statistical measure.
B) It measures the relationship between two securities' returns.
C) It determines the causes of the relationship between two securities' returns.
D) All of these are true.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
7
Which of the following correlation coefficients would provide the greatest benefit for diversification?
A) a perfectly positive correlation coefficient
B) a mildly positive correlation coefficient
C) a correlation coefficient equal to zero
D) a perfectly negative correlation coefficient
A) a perfectly positive correlation coefficient
B) a mildly positive correlation coefficient
C) a correlation coefficient equal to zero
D) a perfectly negative correlation coefficient

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
8
Which of the following portfolios has the greatest reduction of risk?
A) A portfolio with securities all having positive correlation with each other.
B) A portfolio with securities all having zero correlation with each other.
C) A portfolio with securities all having negative correlation with each other.
D) A portfolio with securities all having skewed correlation with each other.
A) A portfolio with securities all having positive correlation with each other.
B) A portfolio with securities all having zero correlation with each other.
C) A portfolio with securities all having negative correlation with each other.
D) A portfolio with securities all having skewed correlation with each other.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
9
Which of the following equations shows the relationship between the correlation coefficient and the covariance:
A) AB = AB A B
B) AB = AB/ A B
C) AB = AB A B
D) AB = A B/ AB
A) AB = AB A B
B) AB = AB/ A B
C) AB = AB A B
D) AB = A B/ AB

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
10
In order to deal with the computational difficulties and complexities of the Markowitz full covariance model, William Sharper developed:
A) the Arbitrage Pricing Theory.
B) the Single Index Model.
C) the Dividend Discount Model.
D) the Binomial Option Pricing Model.
A) the Arbitrage Pricing Theory.
B) the Single Index Model.
C) the Dividend Discount Model.
D) the Binomial Option Pricing Model.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
11
When attempting random diversification, the addition of more stocks to a portfolio that are not perfectly positively correlated will:
A) increase the riskiness of the portfolio.
B) decrease the riskiness of the portfolio but not eliminate it.
C) have no effect on the riskiness of the portfolio.
D) increase the systematic risk but have no effect on the unsystematic risk.
A) increase the riskiness of the portfolio.
B) decrease the riskiness of the portfolio but not eliminate it.
C) have no effect on the riskiness of the portfolio.
D) increase the systematic risk but have no effect on the unsystematic risk.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
12
Given the following probability distribution, calculate the expected return of security XYZ.

A) 16 per cent
B) 22 per cent
C) 25 per cent
D) 18 per cent

A) 16 per cent
B) 22 per cent
C) 25 per cent
D) 18 per cent

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
13
Calculate the risk (standard deviation) of the following two-security portfolio if the correlation coefficient between the two securities is equal to 0.5.
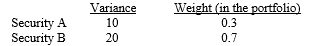
A) 17.0 per cent
B) 5.4 per cent
C) 2.0 per cent
D) 3.7 per cent
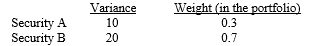
A) 17.0 per cent
B) 5.4 per cent
C) 2.0 per cent
D) 3.7 per cent

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
14
Markowitz's main contribution to the study of modern portfolio theory is:
A) that risk is best measured by subjective assessment.
B) that risk can be best measured for individual assets but has limited applications in portfolios.
C) risk while measured in the past is not quantifiable for use in the future.
D) the measurement of portfolio risk through the use of variance and covariance statistics.
A) that risk is best measured by subjective assessment.
B) that risk can be best measured for individual assets but has limited applications in portfolios.
C) risk while measured in the past is not quantifiable for use in the future.
D) the measurement of portfolio risk through the use of variance and covariance statistics.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
15
Two securities that exhibit statistical independence of returns would have a:
A) positive correlation coefficient.
B) negative correlation coefficient.
C) zero correlation coefficient.
D) zero standard deviation.
A) positive correlation coefficient.
B) negative correlation coefficient.
C) zero correlation coefficient.
D) zero standard deviation.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
16
Which of the following statements regarding correlations among domestic stocks is true?
A) Correlation is generally positive.
B) Correlation is generally negative.
C) Correlation is generally zero.
D) Correlation is generally unstable.
A) Correlation is generally positive.
B) Correlation is generally negative.
C) Correlation is generally zero.
D) Correlation is generally unstable.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
17
Which of the following methods measure the risk of securities?
A) Negative opportunity returns
B) Deviation below zero
C) Standard deviation
D) Range
A) Negative opportunity returns
B) Deviation below zero
C) Standard deviation
D) Range

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
18
Which of the following conditions will result in the greatest amount of risk reduction if an investor were to purchase two securities instead of one for inclusion in a portfolio?
A) The assets are positively correlated with each other.
B) The assets are independent of each other.
C) The assets are negatively correlated with each other.
D) The assets are in the same risk category, e.g., blue chips.
A) The assets are positively correlated with each other.
B) The assets are independent of each other.
C) The assets are negatively correlated with each other.
D) The assets are in the same risk category, e.g., blue chips.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
19
If two stocks had a correlation coefficient between them that decreased over time from a mildly positive correlation to zero correlation, all else remaining constant, the portfolio's risk would:
A) decrease.
B) increase.
C) be negative.
D) remain constant.
A) decrease.
B) increase.
C) be negative.
D) remain constant.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
20
According to Markowitz's mean-variance model, the variance of a portfolio is equal to the weighted:
A) average of the individual variances.
B) covariances between all unique pairs of securities.
C) variances plus the weighted covariances of all pairs of securities.
D) covariances plus the weighted betas of the securities.
A) average of the individual variances.
B) covariances between all unique pairs of securities.
C) variances plus the weighted covariances of all pairs of securities.
D) covariances plus the weighted betas of the securities.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
21
Select the true statement from among the following:
A) The risk for a portfolio is a weighted average of individual security risks.
B) Portfolio risk accounts for the correlation between securities in the portfolio as well as the proportion of each security in the portfolio.
C) Having established the portfolio weights, the calculation of the expected return depends on the calculation of portfolio risk.
D) When adding a security to a portfolio, the average covariance between it and the other securities is not important.
A) The risk for a portfolio is a weighted average of individual security risks.
B) Portfolio risk accounts for the correlation between securities in the portfolio as well as the proportion of each security in the portfolio.
C) Having established the portfolio weights, the calculation of the expected return depends on the calculation of portfolio risk.
D) When adding a security to a portfolio, the average covariance between it and the other securities is not important.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
22
Probability distributions represent:
A) the absolute dollar amounts that will be returned from an investment in the future.
B) the percentage returns that will be returned from an investment in the future.
C) the likelihood of various outcomes being typically expressed as decimals or fractions.
D) the chance that returns on an investment will be inversely related to interest rates.
A) the absolute dollar amounts that will be returned from an investment in the future.
B) the percentage returns that will be returned from an investment in the future.
C) the likelihood of various outcomes being typically expressed as decimals or fractions.
D) the chance that returns on an investment will be inversely related to interest rates.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
23
In a normal distribution the girth of the distribution is the:
A) mean.
B) median.
C) mode.
D) standard deviation.
A) mean.
B) median.
C) mode.
D) standard deviation.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
24
Random diversification:
A) generally leads to optimal diversification.
B) does not lead to any diversification.
C) is the first step in the Markowitz portfolio selection model.
D) generally does not lead to optimal diversification.
A) generally leads to optimal diversification.
B) does not lead to any diversification.
C) is the first step in the Markowitz portfolio selection model.
D) generally does not lead to optimal diversification.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
25
In Markowitz's theory, the risk of a portfolio is measured by:
A) its beta.
B) its systematic risk.
C) its standard deviation.
D) its nonsystematic risk.
A) its beta.
B) its systematic risk.
C) its standard deviation.
D) its nonsystematic risk.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
26
Concerning the riskiness of a portfolio of two securities, using the Markowitz model, select the false statement.
A) The riskiness depends on the variability of the securities.
B) The riskiness depends on the percentage of portfolio assets invested in each security.
C) The riskiness depends on the expected return of each security.
D) The riskiness depends on the amount of correlation among the security returns.
A) The riskiness depends on the variability of the securities.
B) The riskiness depends on the percentage of portfolio assets invested in each security.
C) The riskiness depends on the expected return of each security.
D) The riskiness depends on the amount of correlation among the security returns.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
27
The Markowitz model is primarily concerned with providing estimates of the beta for a portfolio.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
28
A probability distribution shows only the likely outcomes that may occur but not the probabilities associated with these likely outcomes.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
29
Portfolio return is a weighted average of the returns on the individual securities.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
30
A negative correlation coefficient indicates that the returns of two securities have a tendency to move in the same direction.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
31
As the number of securities held in a portfolio increases, the importance of each individual security's risk decreases.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
32
As the number of securities held in a portfolio increases, the importance of the covariance relationships decreases.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
33
The benefits of random diversification continue to increase as long as more securities are added to the portfolio.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
34
What is the range of the correlation coefficient and how is it important in choosing securities for inclusion in a portfolio?

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
35
Give an example of two industries that might exhibit low correlation of returns. Give an example that might exhibit high correlation.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
36
How many securities would a portfolio manager need to form a well-diversified portfolio? Why might the number of securities change over time?

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
37
A portfolio consisting of two securities with perfect negative correlation with the appropriate weights of each security can be derived to exhibit a standard deviation of zero which makes it risk-free. What makes this riskless portfolio impossible to achieve in the real world?

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
38
Your rich uncle comments that he never invests in foreign stocks because they are too risky. Although reluctant to argue with success, what could you tell him about the effect of international diversification on a portfolio containing both domestic and foreign securities?

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
39
Conventional wisdom has long held that diversification of a stock portfolio should be across industries or inter-industry diversification as opposed to diversification within an industry or intra-industry diversification. Does the correlation coefficient indirectly recommend the same thing?

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
40
Calculate the expected return and risk (standard deviation) for General Fudge for 200X, given the following information:
Probabilities

Probabilities


Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
41
Three securities have the following expected returns: X = 10 per cent, Y = 18 per cent, and Z = 25 per cent.
(a) Calculate the expected return for a portfolio consisting of all three securities if equal amounts are placed in each security.
(b) Assume that the standard deviations for these three securities are, respectively, 12 per cent, 14 per cent, and 18 per cent. The correlation coefficients are as follows: XY = +.6, YZ = +.2, and XZ = -.3. Assuming equal weights, calculate the standard deviation for the portfolio.
(a) Calculate the expected return for a portfolio consisting of all three securities if equal amounts are placed in each security.
(b) Assume that the standard deviations for these three securities are, respectively, 12 per cent, 14 per cent, and 18 per cent. The correlation coefficients are as follows: XY = +.6, YZ = +.2, and XZ = -.3. Assuming equal weights, calculate the standard deviation for the portfolio.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
42
Given an expected market return of 12 per cent, with a standard deviation of 20 per cent, and the following data:
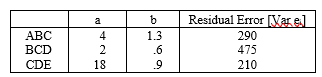
(a) Calculate the expected return for stock ABC using the single-index model.
(b) Calculate the variance for stock CDE using the single-index model.

(a) Calculate the expected return for stock ABC using the single-index model.
(b) Calculate the variance for stock CDE using the single-index model.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
43
Assume that the expected return on the S&P/TSX Composite Index is 12 per cent with a standard deviation of 16 per cent. Given the following information for stocks A, B, and C and the single index model:
(a) Calculate the expected return for each stock.
(b) Calculate the variance and standard deviation for each stock.
(c) Indicate which of the three securities is the riskiest and which is least risky when added to a well-diversified portfolio.
(a) Calculate the expected return for each stock.
(b) Calculate the variance and standard deviation for each stock.
(c) Indicate which of the three securities is the riskiest and which is least risky when added to a well-diversified portfolio.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
44
(a) Use the single-index model to calculate the expected return of a portfolio composed of the following four securities:
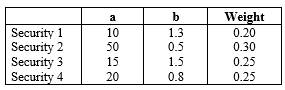
ERm = 15 per cent
Standard Deviation of the market index = 20 per cent
(b) What is the systematic risk associated with the expected return of the four-security portfolio?

ERm = 15 per cent
Standard Deviation of the market index = 20 per cent
(b) What is the systematic risk associated with the expected return of the four-security portfolio?

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck



