Deck 7: Advanced Regression Analysis
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/52
Play
Full screen (f)
Deck 7: Advanced Regression Analysis
1
In a regression model, the __________ exists when a predictor variable has a different partial effect on the outcome of another predictor variable.
A) target effect
B) interaction effect
C) dummy effect
D) predictor effect
A) target effect
B) interaction effect
C) dummy effect
D) predictor effect
interaction effect
2
What is the predicted value ( ) when the numerical variable is x = 70 for the regression equation = ?831 + 29.0x ? 0.113x2?
A) 1,967.7
B) 1,454.2
C) 645.3
D) Not enough sufficient data to calculate the predicted value.
A) 1,967.7
B) 1,454.2
C) 645.3
D) Not enough sufficient data to calculate the predicted value.
645.3
3
What is the predicted value ( ) when the numerical variable is x = 70 for the regression equation = -810 + 24.4x - 0.142x2?
A) 1822.2
B) 1593.8
C) 202.2
D) Not enough sufficient data to calculate the predicted value.
A) 1822.2
B) 1593.8
C) 202.2
D) Not enough sufficient data to calculate the predicted value.
202.2
4
A variable with a value of x1x2 is added to the general linear regression model to account for two predictive variables, x1 and x2 and the effect on the response variable. This type of effect is called __________.
A) transformative
B) dummy
C) interaction
D) predictive
A) transformative
B) dummy
C) interaction
D) predictive

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
5
Consider the sample correlation coefficients in the table below. How much of the variability in time can be explained by boxes using the alternative way of to determine the coefficient of determination. 
A) 79%
B) 26.0%
C) 49.4%
D) 57.0%

A) 79%
B) 26.0%
C) 49.4%
D) 57.0%

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
6
Consider the sample correlation coefficients in the table below. How much of the variability in time can be explained by boxes using the alternative way of to determine the coefficient of determination. 
A) 75%
B) 25.5%
C) 49.5%
D) 55.6%

A) 75%
B) 25.5%
C) 49.5%
D) 55.6%

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
7
A study was completed on cholesterol in 100 male adults 40-60 years of age to determine if there is a relationship between cholesterol concentration and time spent watching TV. The researchers wanted to determine if there are any predictive results, such as if the amount of time spent watching TV increases or decreases cholesterol levels. Based on the following regression results, what was the overall study p-value and is it statistically significant? 
A) The p-value = 0.002 and is statistically significant because it is under the 5% level.
B) The p-value = 0.002 and is not statistically significant because it is under the 5% level.
C) The p-value = 0.000 and is statistically significant because it is under the 5% level.
D) The p-value = 0.001 and is statistically significant because it is under the 5% level.

A) The p-value = 0.002 and is statistically significant because it is under the 5% level.
B) The p-value = 0.002 and is not statistically significant because it is under the 5% level.
C) The p-value = 0.000 and is statistically significant because it is under the 5% level.
D) The p-value = 0.001 and is statistically significant because it is under the 5% level.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
8
A study was completed on cholesterol in 100 male adults 40-60 years of age to determine if there is a relationship between cholesterol concentration and time spent watching TV. The researchers wanted to determine if there are any predictive results, such as if the amount of time spent watching TV increases or decreases cholesterol levels. Based on the following regression results, what was the overall study p-value and is it statistically significant? 
A) The p-value = 0.003 and is statistically significant because it is under the 5% level.
B) The p-value = 0.003 and is not statistically significant because it is under the 5% level.
C) The p-value = 0.000 and is statistically significant because it is under the 5% level.
D) The p-value = 0.002 and is statistically significant because it is under the 5% level.

A) The p-value = 0.003 and is statistically significant because it is under the 5% level.
B) The p-value = 0.003 and is not statistically significant because it is under the 5% level.
C) The p-value = 0.000 and is statistically significant because it is under the 5% level.
D) The p-value = 0.002 and is statistically significant because it is under the 5% level.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
9
Consider a linear regression model where y represents the response variable and d1 and d2 represent two dummy variables. The model is estimated as = -2.49 + 1.86x + 3.20d1 - 2.21d2 + 0.50d1d2. Compute for x = 3, d1 = 1, and d2 = 0.
A) 13.61
B) 3.42
C) 13.17
D) 6.29
A) 13.61
B) 3.42
C) 13.17
D) 6.29

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
10
Consider a linear regression model where y represents the response variable and d1 and d2 represent two dummy variables. The model is estimated as = -2.53 + 2.04x + 4.20d1 - 2.86d2 + 0.68d1d2. Compute for x = 3, d1 = 1, and d2 = 0.
A) 13.53
B) 3.71
C) 12.85
D) 7.79
A) 13.53
B) 3.71
C) 12.85
D) 7.79

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
11
Sam, a marketing manager for XYZ big box stores, is trying to determine if there is a relationship between shelf space (in feet) and sales (in hundreds of dollars). To do this, Sam selected the top 12 producing locations. The regression results produced the following adjusted R2 values: Model 1: 0.8874 and Model 2: 0.6028. Which model is more suitable of a prediction?
A) Model 1
B) Model 2
C) Both are suitable
D) Neither model
A) Model 1
B) Model 2
C) Both are suitable
D) Neither model

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
12
Sam, a marketing manager for XYZ big box stores, is trying to determine if there is a relationship between shelf space (in feet) and sales (in hundreds of dollars). To do this, Sam selected the top 12 producing locations. Using the provided Model 1 results, what is the estimated equation on Sales? 
A) ^Sales = 10.085 + 0.203shelves + 0.074shelf_space
B) ^Sales = -0.203shelves + 0.074shelf_space
C) ^Sales = 0.203shelves + 0.074shelf_space
D) ^Sales = 0.074shelf_space ÷ (2 × 0.203shelves)

A) ^Sales = 10.085 + 0.203shelves + 0.074shelf_space
B) ^Sales = -0.203shelves + 0.074shelf_space
C) ^Sales = 0.203shelves + 0.074shelf_space
D) ^Sales = 0.074shelf_space ÷ (2 × 0.203shelves)

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
13
Sam, a marketing manager for XYZ big box stores, is trying to determine if there is a relationship between shelf space (in feet) and sales (in hundreds of dollars). To do this, Sam selected the top 12 producing locations. Using the provided Model 1 results, what is the estimated equation on Sales? 
A) ^Sales = 10.365 + 0.211shelves + 0.074shelf_space
B) ^Sales = -0.211shelves + 0.074shelf_space
C) ^Sales = 0.211shelves + 0.074shelf_space
D) ^Sales = 0.074shelf_space ÷ (2 × 0.211shelves)

A) ^Sales = 10.365 + 0.211shelves + 0.074shelf_space
B) ^Sales = -0.211shelves + 0.074shelf_space
C) ^Sales = 0.211shelves + 0.074shelf_space
D) ^Sales = 0.074shelf_space ÷ (2 × 0.211shelves)

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
14
Sam, a marketing manager for XYZ big box stores, is trying to determine if there is a relationship between shelf space (in feet) and sales (in hundreds of dollars). To do this, Sam selected the top 12 producing locations. Using the provided Model 1 results, which option best interprets the impact of the coefficients and p-values?

* the p-value
A) The predictor variables are below one offering a negative correlation.
B) All predictor variables are positive with a significant influence on sales.
C) There is no impact presented with the coefficients and p-value results.
D) The p-value offers significant influence where the coefficient provides reduction on sales.

* the p-value
A) The predictor variables are below one offering a negative correlation.
B) All predictor variables are positive with a significant influence on sales.
C) There is no impact presented with the coefficients and p-value results.
D) The p-value offers significant influence where the coefficient provides reduction on sales.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
15
The estimate regression equation for the average cost of widgets is:
^Widgets = 7.33 - 0.2340 Output + 0.1892 Output2. Both predictor variables are statistically significant at 5% level, confirming the quadratic effect. What is the predictive average from an output level of 2 million units to 3 million units?
A) The increase in output units results in a $0.02 decrease in predictive average cost.
B) The increase in output units results in a $0.24 increase in predictive average cost.
C) The increase in output units results in a $0.71 decrease in predictive average cost.
D) The increase in output units results in a $0.71 increase in predictive average cost.
^Widgets = 7.33 - 0.2340 Output + 0.1892 Output2. Both predictor variables are statistically significant at 5% level, confirming the quadratic effect. What is the predictive average from an output level of 2 million units to 3 million units?
A) The increase in output units results in a $0.02 decrease in predictive average cost.
B) The increase in output units results in a $0.24 increase in predictive average cost.
C) The increase in output units results in a $0.71 decrease in predictive average cost.
D) The increase in output units results in a $0.71 increase in predictive average cost.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
16
The estimate regression equation for the average cost of widgets is:
^Widgets = 7.23 - 0.2478 Output + 0.1954 Output2. Both predictor variables are statistically significant at 5% level, confirming the quadratic effect. What is the predictive average from an output level of 2 million units to 3 million units?
A) The increase in output units results in a $0.02 decrease in predictive average cost.
B) The increase in output units results in a $0.24 increase in predictive average cost.
C) The increase in output units results in a $0.73 decrease in predictive average cost.
D) The increase in output units results in a $0.73 increase in predictive average cost.
^Widgets = 7.23 - 0.2478 Output + 0.1954 Output2. Both predictor variables are statistically significant at 5% level, confirming the quadratic effect. What is the predictive average from an output level of 2 million units to 3 million units?
A) The increase in output units results in a $0.02 decrease in predictive average cost.
B) The increase in output units results in a $0.24 increase in predictive average cost.
C) The increase in output units results in a $0.73 decrease in predictive average cost.
D) The increase in output units results in a $0.73 increase in predictive average cost.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
17
Todd uses the quadratic regression model to determine the predictive average unit cost of baseballs produced in his production facility. After determining predictive average costs at multiple unit batch size amounts in millions, he now wants to know what the output level that minimizes his costs would be.
-Given b1 = -0.3600 and b2 = 0.0201, what is the level that will maximize his average cost in units?
A) 7.6 million units
B) 3.3 million units
C) 18.80 million units
D) 8.96 million units
-Given b1 = -0.3600 and b2 = 0.0201, what is the level that will maximize his average cost in units?
A) 7.6 million units
B) 3.3 million units
C) 18.80 million units
D) 8.96 million units

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
18
Todd uses the quadratic regression model to determine the predictive average unit cost of baseballs produced in his production facility. After determining predictive average costs at multiple unit batch size amounts in millions, he now wants to know what the output level that minimizes his costs would be.
- Given b1 = ?0.3802 and b2 = 0.0198, what is the level that will maximize his average cost in units?
A) 7.5 million units
B) 3.7 million units
C) 19.20 million units
D) 9.60 million units
- Given b1 = ?0.3802 and b2 = 0.0198, what is the level that will maximize his average cost in units?
A) 7.5 million units
B) 3.7 million units
C) 19.20 million units
D) 9.60 million units

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
19
Ava Diego, a doctoral student, is researching car loans issued at a local bank. She prepared a sample of 200 to determine if there is a relationship between the loan amount, length of the loan, and interest rate provided. The regression results are in the table below. Which model is more suitable for prediction and what is the best fit reason? 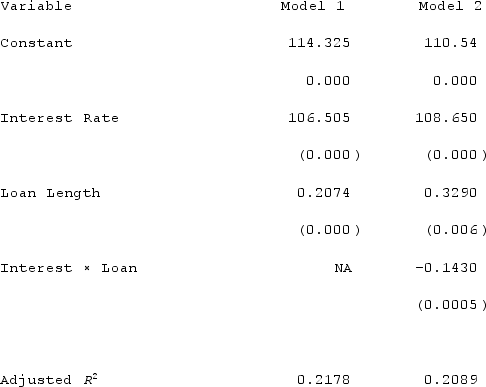
A) Model 2 is the most suitable because of the p-value variance.
B) Model 1 is the most suitable because of the higher adjusted R2 value.
C) Model 2 is the most suitable because of the lower adjusted R2 value.
D) Neither provide enough results data to predict the model or reasoning.

A) Model 2 is the most suitable because of the p-value variance.
B) Model 1 is the most suitable because of the higher adjusted R2 value.
C) Model 2 is the most suitable because of the lower adjusted R2 value.
D) Neither provide enough results data to predict the model or reasoning.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
20
An estimated linear regression of annual fuel expenditures y on annual income x is represented as the following equation: = 2,700 + 0.02x. What is the estimated slope coefficient value?
A) 0.02
B) 2b1 + 0.02
C) 54
D) 54x
A) 0.02
B) 2b1 + 0.02
C) 54
D) 54x

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
21
An estimated linear regression of annual fuel expenditures y on annual income x is represented as the following equation: y= 2,200 + 0.05x. What is the estimated slope coefficient value?
A) 0.05
B) 2b1 + 0.05
C) 110
D) 110x
A) 0.05
B) 2b1 + 0.05
C) 110
D) 110x

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
22
An estimated linear regression of annual fuel expenditures y on annual income x is represented as the following equation: y= 2,200 + 0.05x. Jim was offered a new job that would increase his salary by $2,000. What would be his potential increase in fuel costs? Based on this information, is the assumption of increased fuel cost against annual salary meaningful?
A) The increase in fuel cost is $100.00 annually; linearity assumption is justified.
B) The increase in fuel cost is $100.00 annually; linearity assumption is not justified.
C) The increase in fuel cost is $50.00 annually; linearity assumption is justified.
D) The increase in fuel cost is $1000.00 annually; linearity assumption is not justified.
A) The increase in fuel cost is $100.00 annually; linearity assumption is justified.
B) The increase in fuel cost is $100.00 annually; linearity assumption is not justified.
C) The increase in fuel cost is $50.00 annually; linearity assumption is justified.
D) The increase in fuel cost is $1000.00 annually; linearity assumption is not justified.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
23
In the following logarithmic regression model, 1 × 0.01 measures the approximate unit change in E(y) when x increases. If 1 = 11,500, then what is the unit change in E(y)?
A) 11.5 units
B) 1,150 units
C) 115 units
D) 11,500 units
A) 11.5 units
B) 1,150 units
C) 115 units
D) 11,500 units

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
24
In the following logarithmic regression model, 1 × 0.01 measures the approximate unit change in E(y) when x increases. If 1 = 6,000, then what is the unit change in E(y)?
A) 6 units
B) 600 units
C) 60 units
D) 6,000 units
A) 6 units
B) 600 units
C) 60 units
D) 6,000 units

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
25
In an exponential regression model, the exact percentage of change can be calculated as: (exp( 1) - 1) × 100. If 1 = 0.23, what is the percent increase in E(y)?
A) 25%
B) 26%
C) 75%
D) 22%
A) 25%
B) 26%
C) 75%
D) 22%

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
26
In an exponential regression model, the exact percentage of change can be calculated as: (exp( 1) - 1) × 100. If 1 = 0.25, what is the percent increase in E(y)?
A) 25%
B) 28%
C) 75%
D) 22%
A) 25%
B) 28%
C) 75%
D) 22%

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
27
In the model y = 0 + 1ln(x) + , the predicted value is 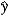 = b0 + b1ln(x). What is the impact of the estimated slope coefficient?
= b0 + b1ln(x). What is the impact of the estimated slope coefficient?
A) b1 measures the approximate change in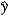 when x increases by 1 unit.
when x increases by 1 unit.
B) b1 × 0.01 measures the approximate change in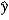 when x increases by 1%.
when x increases by 1%.
C) b1 measures the approximate change in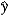 when x increases by 1%.
when x increases by 1%.
D) b1 × 100 measures the approximate change in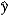 when x increases by 1 unit.
when x increases by 1 unit.
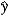 = b0 + b1ln(x). What is the impact of the estimated slope coefficient?
= b0 + b1ln(x). What is the impact of the estimated slope coefficient?A) b1 measures the approximate change in
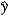 when x increases by 1 unit.
when x increases by 1 unit.B) b1 × 0.01 measures the approximate change in
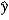 when x increases by 1%.
when x increases by 1%.C) b1 measures the approximate change in
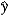 when x increases by 1%.
when x increases by 1%.D) b1 × 100 measures the approximate change in
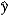 when x increases by 1 unit.
when x increases by 1 unit.
Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
28
In the model y = 0 + 1x + , the predicted value is  = b0 + b1x. What is the impact of the estimated slope coefficient?
= b0 + b1x. What is the impact of the estimated slope coefficient? 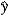
A) b1 measures the approximate change in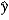 when x increases by 1 unit.
when x increases by 1 unit.
B) b1 × 0.01 measures the approximate change in when x increases by 1%.
when x increases by 1%.
C) b1 measures the approximate change in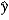 when x increases by 1%.
when x increases by 1%.
D) b1 × 100 measures the approximate change in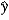 when x increases by 1 unit.
when x increases by 1 unit.
 = b0 + b1x. What is the impact of the estimated slope coefficient?
= b0 + b1x. What is the impact of the estimated slope coefficient? 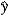
A) b1 measures the approximate change in
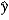 when x increases by 1 unit.
when x increases by 1 unit.B) b1 × 0.01 measures the approximate change in
 when x increases by 1%.
when x increases by 1%.C) b1 measures the approximate change in
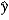 when x increases by 1%.
when x increases by 1%.D) b1 × 100 measures the approximate change in
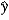 when x increases by 1 unit.
when x increases by 1 unit.
Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
29
In the model ln(y) = 0 + 1x + , the predicted value is 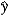 = exp (b0 + b1x +
= exp (b0 + b1x +  ÷ 2). What is the impact of the estimated slope coefficient?
÷ 2). What is the impact of the estimated slope coefficient?
A) b1 measures the approximate change in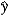 when x increases by 1 unit.
when x increases by 1 unit.
B) b1 × 0.01 measures the approximate change in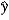 when x increases by 1%.
when x increases by 1%.
C) b1 measures the approximate change in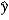 when x increases by 1%.
when x increases by 1%.
D) b1 × 100 measures the approximate change in when x increases by 1 unit.
when x increases by 1 unit.
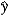 = exp (b0 + b1x +
= exp (b0 + b1x +  ÷ 2). What is the impact of the estimated slope coefficient?
÷ 2). What is the impact of the estimated slope coefficient?A) b1 measures the approximate change in
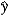 when x increases by 1 unit.
when x increases by 1 unit.B) b1 × 0.01 measures the approximate change in
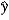 when x increases by 1%.
when x increases by 1%.C) b1 measures the approximate change in
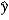 when x increases by 1%.
when x increases by 1%.D) b1 × 100 measures the approximate change in
 when x increases by 1 unit.
when x increases by 1 unit.
Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
30
Consider the following quadratic model, y^= 30 + 1.50x ? 0.25x2. Predict y when x = 14.
A) 2
B) 40
C) 12
D) 9
A) 2
B) 40
C) 12
D) 9

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
31
<p>Consider the following quadratic model,  = 25 + 1.5x ? 0.25x2. Predict y when x = 12.
= 25 + 1.5x ? 0.25x2. Predict y when x = 12.
A) 40
B) 12
C) 9
D) 7
 = 25 + 1.5x ? 0.25x2. Predict y when x = 12.
= 25 + 1.5x ? 0.25x2. Predict y when x = 12.A) 40
B) 12
C) 9
D) 7

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
32
Consider a binary response variable y and a predictor variable x that varies between 0 and 5. The linear model is estimated as 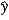 = -2.90 + 0.65x. What is the estimated probability for x = 5?
= -2.90 + 0.65x. What is the estimated probability for x = 5?
A) 0.35
B) 6.15
C) 0.65
D) -6.15
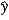 = -2.90 + 0.65x. What is the estimated probability for x = 5?
= -2.90 + 0.65x. What is the estimated probability for x = 5?A) 0.35
B) 6.15
C) 0.65
D) -6.15

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
33
Christian Za is using the holdout method to partition his data into two independent and mutually exclusive sets: 75% in a training set and 25% in a validation set. Based on an R2 value of 0.4532 and RMSE of 0.3268 for the training set and an R2 value of 0.1426 and RMSE of 0.5371 for the validation set, which of the competing models is the preferred model?
A) The validation data set would be the preferred model.
B) The training data set would be the preferred model.
C) Both models are preferred models.
D) There is not enough data to determine the preferred model.
A) The validation data set would be the preferred model.
B) The training data set would be the preferred model.
C) Both models are preferred models.
D) There is not enough data to determine the preferred model.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
34
Using a sample of 50, the following regression output is obtained from estimating the linear probability regression model y = 0 + 1x + . What is the predicted probability when x = 14? 
A) 4.42
B) 143.90
C) 3.86
D) 0.72

A) 4.42
B) 143.90
C) 3.86
D) 0.72

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
35
Using a sample of 50, the following regression output is obtained from estimating the linear probability regression model y = 0 + 1x + . What is the predicted probability when x = 14? 
A) 4.42
B) 3.86
C) 8.34
D) 0.72

A) 4.42
B) 3.86
C) 8.34
D) 0.72

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
36
The following table contains the parameter estimates of the linear probability regression model and the logistic regression model. When considering a binary response variable y and two predictor variables, x1 and x2, what is the predicted probability implied by the logistic regression model for x1 = 2 with x2 = 15? (Hint: for logit, the model is = exp(b0+ b1x1 + b2x2)1 + exp(b0 + b1x1 + b2x2).exp(b0+ b1x1 + b2x21 + expb0 + b1x1 + b2x2.) 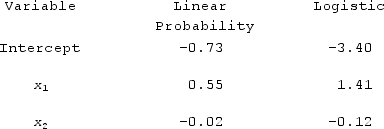
A) 0.006
B) 0.085
C) -5.160
D) 0.005

A) 0.006
B) 0.085
C) -5.160
D) 0.005

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
37
The following table contains the parameter estimates of the linear probability regression model and the logistic regression model. When considering a binary response variable y and two predictor variables, x1 and x2, what is the predicted probability implied by the logistic regression model for x1 = 2 with x2 = 15? (Hint: for logit, the model is = 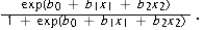 ) < / p >
) < / p > 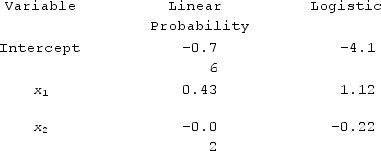
A) 0.838
B) 0.006
C) -5.16
D) 0.005
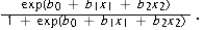 ) < / p >
) < / p > 
A) 0.838
B) 0.006
C) -5.16
D) 0.005

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
38
The following table contains the parameter estimates of the linear probability regression model and the logistic regression model. When considering a binary response variable y and two predictor variables, x1 and x2, What is the estimated linear probability implied by the logistic probability regression model for x1 = 3 with x2 = 9? 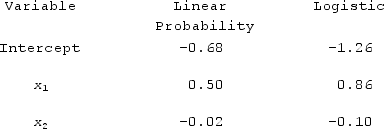
A) 1.87
B) 0.35
C) 0.64
D) -0.87

A) 1.87
B) 0.35
C) 0.64
D) -0.87

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
39
The following table contains the parameter estimates of the linear probability regression model and the logistic regression model. When considering a binary response variable y and two predictor variables, x1 and x2, What is theestimated linear probabilityimplied by the logistic probability regression model for x1 = 3 with x2 = 9? 
A) 1.87
B) -0.35
C) 0.35
D) -0.87

A) 1.87
B) -0.35
C) 0.35
D) -0.87

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
40
A regression model made to conform to a sample set of data, compromising predictive power is called __________.
A) cross-validation
B) flooding
C) overfitting
D) binary choice
A) cross-validation
B) flooding
C) overfitting
D) binary choice

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
41
A linear regression model applied to a binary response variable is called a __________.
A) logistic regression model
B) log-transformed model
C) log-log regression model
D) linear probability regression model
A) logistic regression model
B) log-transformed model
C) log-log regression model
D) linear probability regression model

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
42
Which interpretation of a linear probability regression model represents the estimate ^P = -40 + 0.05x?
A) for each 1 unit increase in x, the predicted probability ^P decreases by 0.05.
B) for each 40 unit decrease in x, the predicted probability ^P increases by 40.
C) for each 1 unit increase in x, the predicted probability ^P increases by 0.05.
D) for each 0.05 unit increase in x, the predicted probability ^P decreases by 40.
A) for each 1 unit increase in x, the predicted probability ^P decreases by 0.05.
B) for each 40 unit decrease in x, the predicted probability ^P increases by 40.
C) for each 1 unit increase in x, the predicted probability ^P increases by 0.05.
D) for each 0.05 unit increase in x, the predicted probability ^P decreases by 40.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
43
In cross-validation, if k equals the sample size, the resulting method is also called __________.
A) sensitive data cross-validation method
B) the leave-one-out cross-validation method
C) equality cross-validation method
D) partition cross-validation method
A) sensitive data cross-validation method
B) the leave-one-out cross-validation method
C) equality cross-validation method
D) partition cross-validation method

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
44
In using both the linear probability regression and the logistic regression models for n = 40, the following table is the analysis of the holdout method. Based on the table, what is the impact of changing the to binary predictions? 
A) There is no relevant outcome changing ? to a binary variable.
B) By comparing to y, the validation results are not able to be validated.
C) By comparing to y, the accuracy of the model is 100%, but can change with a larger validation set.
D) By comparing to y, the accuracy of the model is 100% and will not change based on a larger validation set.

A) There is no relevant outcome changing ? to a binary variable.
B) By comparing to y, the validation results are not able to be validated.
C) By comparing to y, the accuracy of the model is 100%, but can change with a larger validation set.
D) By comparing to y, the accuracy of the model is 100% and will not change based on a larger validation set.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
45
In determining the partial effect on dummy variable d in a regression model with an interaction variable = b0 + b1x + b2d + b3xd, the numeric variable x value needs to be known.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
46
In a regression model with two dummy variables and an interaction variable d1d2:y = 0 + 1d1 + 2d2 + 3d1d2 + , the interaction variables are easy to estimate.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
47
In the quadratic regression model, if 2 > 0 then the relationship between x and y is an inverted U-shape.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
48
ln(y) = 0 + 1 ln(x) + represents the exponential regression model.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
49
In the linear probability regression model, the response variable y will equal 1 or 0 to represent the probability of success.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
50
To test for the accuracy rate in a binary choice model, the number of correct classification observations for both outcomes should be reported.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
51
In the k-fold cross-validation method, the smaller the k value, the greater the reliability of the k-fold method.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
52
Because software packages use random draws of the observations to partition data, the results will not be identical to a fixed partitioning of the observations.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck



