Deck 4: Probability and Probability Distributions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/50
Play
Full screen (f)
Deck 4: Probability and Probability Distributions
1
What is the probability when a personal assessment is made without referencing data?
A) empirical probability
B) classical probability
C) subjective probability
D) exclusive probability
A) empirical probability
B) classical probability
C) subjective probability
D) exclusive probability
subjective probability
2
The union of two events is denoted as
A) A S.
B) A B.
C) P(A B).
D) A B.
A) A S.
B) A B.
C) P(A B).
D) A B.
A B.
3
Which rule is being followed when summing P(A) and P(B) then subtracting P(A B) from the sum?
A) complement
B) multiplication
C) addition
D) joint probability
A) complement
B) multiplication
C) addition
D) joint probability
addition
4
Mutually exclusive events __________.
A) have joint probability of zero
B) contain the multiple of two probabilities
C) are conditional on interest
D) contain all possible experiment outcomes
A) have joint probability of zero
B) contain the multiple of two probabilities
C) are conditional on interest
D) contain all possible experiment outcomes

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
5
Using conditional probability, if P(A) = 0.60, P(B) = 0.25, and P(A B) = 0.05, then P(A | B) =
A) 0.40.
B) 0.08.
C) 0.20.
D) 5.00.
A) 0.40.
B) 0.08.
C) 0.20.
D) 5.00.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
6
Using conditional probability, if P(A) = 0.50, P(B) = 0.20, and P(A B) = 0.15, then P(A | B) =
A) 0.40.
B) 0.30.
C) 0.75.
D) 2.5.
A) 0.40.
B) 0.30.
C) 0.75.
D) 2.5.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
7
In Holland, 72% of the people own a car. If five adults are randomly selected, what is the probability that none of the four have a car?
A) 4.93%
B) 0.61%
C) 23.60%
D) 0.62%
A) 4.93%
B) 0.61%
C) 23.60%
D) 0.62%

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
8
In Holland, 60% of the people own a car. If five adults are randomly selected, what is the probability that none of the five have a car?
A) 7.8%
B) 1.02%
C) 40%
D) 1.03%
A) 7.8%
B) 1.02%
C) 40%
D) 1.03%

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
9
In Holland, 30% of the people own a car. If five adults are randomly selected, what is the probability that no more than two own a car?
A) 37.2% probability that more than two own a car.
B) 30.9% probability that more than two own a car.
C) 66.8% probability that no more than two own a car.
D) 83.7% probability that no more than two own a car.
A) 37.2% probability that more than two own a car.
B) 30.9% probability that more than two own a car.
C) 66.8% probability that no more than two own a car.
D) 83.7% probability that no more than two own a car.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
10
A simple event _____.
A) contains unlimited outcomes
B) contains exactly two outcomes
C) contains only subsets of the outcome
D) contains a single outcome
A) contains unlimited outcomes
B) contains exactly two outcomes
C) contains only subsets of the outcome
D) contains a single outcome

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
11
Michael has interviewed for two jobs. He feels that he has a 56% chance of getting an offer on Job A and a 60% chance of getting an offer on Job B. He also believes there is a 60% chance of getting an offer on both jobs. What is the probability that he receives an offer on at least one of the jobs?
A) 0.60
B) 0.25
C) 0.10
D) 0.56
A) 0.60
B) 0.25
C) 0.10
D) 0.56

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
12
Michael has interviewed for two jobs. He feels that he has a 65% chance of getting an offer on Job A and a 45% chance of getting an offer on Job B. He also believes there is a 40% chance of getting an offer on both jobs. What is the probability that he receives an offer on at least one of the jobs?
A) 0.60
B) 0.25
C) 0.10
D) 0.70
A) 0.60
B) 0.25
C) 0.10
D) 0.70

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
13
Michael has interviewed for two jobs. He feels that he has a 65% chance of getting an offer on job A and a 45% chance of getting an offer on job B. He also believes there is a 40% chance of getting an offer on both jobs. What is the probability that he does not get an offer at either job?
A) 0.10
B) 0.30
C) 0.70
D) 0.25
A) 0.10
B) 0.30
C) 0.70
D) 0.25

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
14
Two events are _____ if the occurrence of one event does not affect the probability occurrence of another.
A) simple
B) dependent
C) independent
D) comparative
A) simple
B) dependent
C) independent
D) comparative

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
15
Which is not a characteristic of the normal distribution?
A) It is bell-shaped.
B) It is inverse.
C) It is asymptotic.
D) It is symmetric.
A) It is bell-shaped.
B) It is inverse.
C) It is asymptotic.
D) It is symmetric.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
16
Simone, owner of the Blue Canoe Coffee Shop, ran a report showing the identified valued customer visits the shop on average 12 times in a 60-day period. Simone now wants to break down the information further to determine how many visits she should expect in a 5-day period from a tracked value customer. How many visits should Simone expect?
A) 1
B) 3
C) 2
D) 4
A) 1
B) 3
C) 2
D) 4

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
17
Simone, owner of the Blue Canoe Coffee Shop, ran a report showing the identified valued customer visits the shop on average 18 times in a 30-day period. Simone now wants to break down the information further to determine how many visits she should expect in a 5-day period from a tracked value customer. How many visits should Simone expect?
A) 3
B) 5
C) 1
D) 4
A) 3
B) 5
C) 1
D) 4

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
18
A special case where the mean is equal to zero and the variance is equal to one is called _____.
A) normal distribution
B) standard normal distribution
C) corresponding value
D) standard normal variable
A) normal distribution
B) standard normal distribution
C) corresponding value
D) standard normal variable

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
19
Alex has been studying for the certified management exam. Results from the last exam indicate that the mean was 62 with a standard deviation of 5. He needs to be in the top 20% (80th percentile) to pass. Use zvalue with two decimal places, 1.28, in your calculations. What score will place Alex in the top 20% of the distribution?
A) 68.40
B) 79.68
C) 83.12
D) 74.00
A) 68.40
B) 79.68
C) 83.12
D) 74.00

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
20
Alex has been studying for the certified management exam. Results from the last exam indicate that the mean was 72 with a standard deviation of 6. He needs to be in the top 20% (80th percentile) to pass. The z table indicates 1.28. What score will place Alex in the top 20% of the distribution?
A) 79.68
B) 83.12
C) 74
D) 79.28
A) 79.68
B) 83.12
C) 74
D) 79.28

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
21
The Daytona 500 runs 40 race cars. Of the 40, 19 cars crashed. This is a probability of 0.475 that a car will crash in the race. This is an example of which probability?
A) subjective
B) empirical
C) classical
D) random
A) subjective
B) empirical
C) classical
D) random

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
22
Which is the best probability to determine the outcome of rolling seven with two dice?
A) subjective
B) empirical
C) classical
D) random
A) subjective
B) empirical
C) classical
D) random

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
23
Which one does not satisfy the Poisson process?
A) Success is presented as an integer between one and infinity.
B) Number of successes counted in nonoverlapping intervals are independent.
C) The interval is the same for probability failure as in success in exceeding the size of the interval.
D) Probability of success in an interval is the same for all intervals of equal size and proportionality.
A) Success is presented as an integer between one and infinity.
B) Number of successes counted in nonoverlapping intervals are independent.
C) The interval is the same for probability failure as in success in exceeding the size of the interval.
D) Probability of success in an interval is the same for all intervals of equal size and proportionality.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
24
Events are considered _____ if they include all outcomes in the sample space.
A) posterior
B) exhaustive
C) a sample
D) a rule
A) posterior
B) exhaustive
C) a sample
D) a rule

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
25
The intersection of two events is denoted as __________.
A) A B
B) A B
C) P (A B) ²
D) P (Ac) = 1 - P(A)
A) A B
B) A B
C) P (A B) ²
D) P (Ac) = 1 - P(A)

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
26
Marketing analysis determined 49% of females between the ages of 25 and 34 years search for green technology and practice being green, as compared to 37% of men in the same age group. What is the probability that a randomly selected woman between the age of 25 and 34 does not search for green technology?
A) 68% probability
B) 56% probability
C) 51% probability
D) 44% probability
A) 68% probability
B) 56% probability
C) 51% probability
D) 44% probability

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
27
Marketing analysis determined 44% of females between the ages of 25 and 34 years search for green technology and practice being green, as compared to 32% of men in the same age group. What is the probability that a randomly selected woman between the age of 25 and 34 does not search for green technology?
A) 12% probability
B) 68% probability
C) 56% probability
D) 44% probability
A) 12% probability
B) 68% probability
C) 56% probability
D) 44% probability

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
28
Marketing analysis determined 55% of females between the ages of 25 to 34 years old search for green technology and practice being green, as compared to 33% of men in the same age group. What is the probability that a randomly selected man between the age of 25 and 34 does not search for green technology?
A) 44% probability
B) 67% probability
C) 12% probability
D) 68% probability
A) 44% probability
B) 67% probability
C) 12% probability
D) 68% probability

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
29
Marketing analysis determined 44% of females between the ages of 25 to 34 years old search for green technology and practice being green, as compared to 32% of men in the same age group. What is the probability that a randomly selected man between the age of 25 and 34 does not search for green technology?
A) 44% probability
B) 68% probability
C) 32% probability
D) 56% probability
A) 44% probability
B) 68% probability
C) 32% probability
D) 56% probability

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
30
The _____ of the discrete random variable X, denoted by E(X), or simply , is a weighted average of all possible values of X.
A) summary value
B) corresponding value
C) random value
D) expected value
A) summary value
B) corresponding value
C) random value
D) expected value

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
31
Howard Simpson at Organics Central Market ran a report showing the identified valued customer visits the market on average 12 times in a 30-day period. Howard now wants to break down the information further to determine how many visits he should expect in a 5-day period from a tracked value customer. What is the probability of a valued customer visiting all 5 days?
A) 4%
B) 10%
C) 8%
D) 9%
A) 4%
B) 10%
C) 8%
D) 9%

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
32
Howard Simpson at Organics Central Market ran a report showing the identified valued customer visits the market on average 18 times in a 30-day period. Howard now wants to break down the information further to determine how many visits he should expect in a 5-day period from a tracked value customer. What is the probability of a valued customer visiting all 5 days?
A) 10%
B) 8%
C) 4%
D) 9%
A) 10%
B) 8%
C) 4%
D) 9%

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
33
Which theorem can the posterior probability be found using the prior probability and conditional probability?
A) Fisher
B) Poisson
C) Bernoulli
D) Bayes'
A) Fisher
B) Poisson
C) Bernoulli
D) Bayes'

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
34
Andrea decided her job opportunities will increase conditional on completing her bachelor's degree. Based on her assumption, what probability would best fit?
A) classical probability
B) conditional probability
C) complement rule
D) empirical probability
A) classical probability
B) conditional probability
C) complement rule
D) empirical probability

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
35
Based on the provided table, the expected employee bonus is 3.05 or 3,050. What is the variance and the standard deviation of the annual bonus amount? 
A) =9.36=3.059
B) =4.95=2.225
C) =9.85=3.138
D) =11.47=3.387

A) =9.36=3.059
B) =4.95=2.225
C) =9.85=3.138
D) =11.47=3.387

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
36
Based on the provided table, the expected employee bonus is 4.95 or 4,950. What is the variance and the standard deviation of the annual bonus amount? 
A)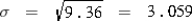
B)
C)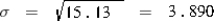
D)

A)
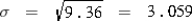
B)

C)
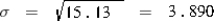
D)


Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
37
Tiffany Ham's business is thriving in Houston, TX. To reward her team, Tiffany is implementing a performance incentive program. Annual Bonuses begin at $5,000 for excellent performance, $3,000 for good performance, and $1,500 for fair performance, and $0 for poor performance.
- The probability levels are 0.10, 0.45, 0.35, and 0.15, respectively. What is the expected value of the annual bonus amount for an employee?
A) $1,875
B) $2,300
C) $2,375
D) $2,325
- The probability levels are 0.10, 0.45, 0.35, and 0.15, respectively. What is the expected value of the annual bonus amount for an employee?
A) $1,875
B) $2,300
C) $2,375
D) $2,325

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
38
Tiffany Ham's business is thriving in Houston, TX. To reward her team, Tiffany is implementing a performance incentive program. Annual Bonuses begin at $5,000 for excellent performance, $3,000 for good performance, and $1,500 for fair performance, and $0 for poor performance.
-The probability levels are 0.15, 0.40, 0.25, and 0.20, respectively. What is the expected value of the annual bonus amount for an employee?
A) $1,875
B) $2,300
C) $2,325
D) $2,375
-The probability levels are 0.15, 0.40, 0.25, and 0.20, respectively. What is the expected value of the annual bonus amount for an employee?
A) $1,875
B) $2,300
C) $2,325
D) $2,375

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
39
In reviewing retirement portfolios, Kim determined the probability of a client owning stock is 0.50 and the probability of owning a bond is 0.20. The probability of a customer who owns bonds already owning stock is 0.55. What is the probability a client owns both securities in their retirement portfolio?
A) 0.30
B) 0.40
C) 0.39
D) 0.28
A) 0.30
B) 0.40
C) 0.39
D) 0.28

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
40
In reviewing retirement portfolios, Kim determined the probability of a client owning stock is 0.70 and the probability of owning a bond is 0.40. The probability of a customer who owns bonds already owning stock is 0.55. What is the probability a client owns both securities in their retirement portfolio?
A) 0.52
B) 0.30
C) 0.40
D) 0.39
A) 0.52
B) 0.30
C) 0.40
D) 0.39

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
41
Alison has been hired to sell two different homes on the same street that two houses apart. She predicts that Home A has a 57% chance in selling on the first week of being listed, whereas Home B is in lesser condition and has a 34% probability. There is also a 14% chance both homes will not sell on the first week of it being listed. What is the probability that house A does not sell given that house B does not sell due to it's poor condition?
A) 0.267
B) 0.212
C) 0.667
D) 0.250
A) 0.267
B) 0.212
C) 0.667
D) 0.250

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
42
Alison has been hired to sell two different homes on the same street that two houses apart. She predicts that Home A has a 75% chance in selling on the first week of being listed, whereas Home B is in lesser condition and has a 30% probability. There is also a 20% chance both homes will not sell on the first week of it being listed. What is the probability that house A does not sell given that house B does not sell due to it's poor condition?
A) 0.267
B) 0.286
C) 0.250
D) 0.700
A) 0.267
B) 0.286
C) 0.250
D) 0.700

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
43
The sample space contains all probable outcomes of an experiment.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
44
If 42% of interns are between the ages of 20 to 25, the complement rule dictates P(Ac) = 1 - P(A) = 1 - 0.42 = 0.58.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
45
According to the total probability rule, P(A) equals the sum of P(A B) and P(A Bc), and is considered conditional on two mutually exclusive and exhaustive events independent of an experiment.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
46
Bayes' theorem is a procedure for updating probabilities based on new information.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
47
A discrete random variable is denoted as distinct countable values x1, x2, x3,…

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
48
A result of attaching probabilities to the outcomes of a Bernoulli process is called a binomial distribution.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
49
The Poisson process is satisfied only if the number of successes counted in nonoverlapping intervals is independent and is not dependent on the proportional size of an interval.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
50
The Gaussian distribution is the most extensively used probability distribution in statistical work.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck



