Deck 8: Rotational Motion and Equilibrium
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/68
Play
Full screen (f)
Deck 8: Rotational Motion and Equilibrium
1
State the difference between pure translational and pure rotational motion.
If an object has only (pure) translational motion every particle in it has the same instantaneous velocity, which means that the object is not rotating. An object may have only (pure) rotational motion - motion about a fixed axis if all of the particles of the object have the same instantaneous angular velocity and travel in circles about the axis of rotation.
2
A car is traveling along a highway at 65 mph. What is the linear speed of the top of the tires?
130 mph
3
A car is traveling along a highway at 65 mph. What is the linear speed of the bottom of the tires?
0 mph
4
Consider a car with its wheels rolling (not sliding) on the road. How fast must the auto move for some point on a wheel to reach the speed of sound? Explain.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
5
State the condition of stable equilibrium.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
6
Is it easier to swing a bat holding the handle at the end, or "choked up"? Why?

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
7
The moment of inertia of a solid sphere about any diameter is 2/5 MR2. What is the moment of inertia about an axis that is tangent to the surface?

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
8
A sphere of radius R and mass M is released from rest, and rolls without slipping down a plane inclined at angle G above horizontal. What is the speed of the sphere after it has moved a distance L?

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
9
The moon has an elliptical orbit around the Earth. The lunar rotational kinetic energy increases as it comes closer to the Earth and decreases as it moves away. What mechanism changes the rotational kinetic energy?

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
10
State the conservation of angular momentum.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
11
The moon causes a tidal bulge on the Earth, and the lunar pull on the bulge slows the rotation velocity of the Earth. Where does the lost angular momentum go?

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
12
Unbalanced torques produce rotational accelerations, and balanced torques produce rotational equilibrium.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
13
If an object is in unstable equilibrium, any small displacement results in a restoring force or torque, which tends to return the object to its original equilibrium position.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
14
The condition for rolling without slipping is that the center of mass speed is
A) Vcm = r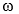 / 2
/ 2
B) Vcm = 2 r 11eea3d6_3beb_76e2_97f4_89bb0fd9c52f_TB9720_11
C) Vcm = r2 11eea3d6_3beb_76e2_97f4_89bb0fd9c52f_TB9720_11
D) Vcm = r 11eea3d6_3beb_76e2_97f4_89bb0fd9c52f_TB9720_11
E) Vcm= r 11eea3d6_3beb_76e2_97f4_89bb0fd9c52f_TB9720_112
A) Vcm = r
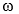 / 2
/ 2B) Vcm = 2 r 11eea3d6_3beb_76e2_97f4_89bb0fd9c52f_TB9720_11
C) Vcm = r2 11eea3d6_3beb_76e2_97f4_89bb0fd9c52f_TB9720_11
D) Vcm = r 11eea3d6_3beb_76e2_97f4_89bb0fd9c52f_TB9720_11
E) Vcm= r 11eea3d6_3beb_76e2_97f4_89bb0fd9c52f_TB9720_112

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
15
Consider a rigid body that is rotating. Which of the following is an accurate statement?
A) All points on the body are moving with the same linear velocity.
B) Its center of rotation must be moving with a constant velocity.
C) Its center of rotation is its center of gravity.
D) Its center of rotation must be at rest, i.e., not moving.
E) All points on the body are moving with the same angular velocity.
A) All points on the body are moving with the same linear velocity.
B) Its center of rotation must be moving with a constant velocity.
C) Its center of rotation is its center of gravity.
D) Its center of rotation must be at rest, i.e., not moving.
E) All points on the body are moving with the same angular velocity.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
16
"Lever Arm" can have which of the following units?
A) N.m2
B) kg. m2 / s
C) kg.m / s2
D) J
E) m
A) N.m2
B) kg. m2 / s
C) kg.m / s2
D) J
E) m

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
17
What condition or conditions is/are necessary for rotational equilibrium?
A)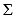 Fy = 0
Fy = 0
B) 11eea3d6_6626_ed43_97f4_99b60549a8af_TB9720_11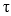 = 0
= 0
C) 11eea3d6_6626_ed43_97f4_99b60549a8af_TB9720_11Fx = 0, 11eea3d6_6626_ed43_97f4_99b60549a8af_TB9720_11Fy = 0
D) 11eea3d6_6626_ed43_97f4_99b60549a8af_TB9720_11Fx = 0, 11eea3d6_6626_ed43_97f4_99b60549a8af_TB9720_11Fy = 0, 11eea3d6_6626_ed43_97f4_99b60549a8af_TB9720_11 11eea3d6_b163_ca86_97f4_73bd7a12183a_TB9720_11 = 0
E) 11eea3d6_6626_ed43_97f4_99b60549a8af_TB9720_11Fx = 0
A)
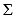 Fy = 0
Fy = 0B) 11eea3d6_6626_ed43_97f4_99b60549a8af_TB9720_11
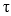 = 0
= 0C) 11eea3d6_6626_ed43_97f4_99b60549a8af_TB9720_11Fx = 0, 11eea3d6_6626_ed43_97f4_99b60549a8af_TB9720_11Fy = 0
D) 11eea3d6_6626_ed43_97f4_99b60549a8af_TB9720_11Fx = 0, 11eea3d6_6626_ed43_97f4_99b60549a8af_TB9720_11Fy = 0, 11eea3d6_6626_ed43_97f4_99b60549a8af_TB9720_11 11eea3d6_b163_ca86_97f4_73bd7a12183a_TB9720_11 = 0
E) 11eea3d6_6626_ed43_97f4_99b60549a8af_TB9720_11Fx = 0

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
18
A pencil balanced on its tip such that it does not move
A) has a zero moment of inertia.
B) is in unstable equilibrium.
C) has a net torque acting on it.
D) has a net vertical force.
E) is in stable equilibrium.
A) has a zero moment of inertia.
B) is in unstable equilibrium.
C) has a net torque acting on it.
D) has a net vertical force.
E) is in stable equilibrium.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
19
Five forces act on a massless rod free to pivot at point P, as shown in Figure 8-1.

Which force is producing a counter-clockwise torque about point P?
A) A
B) B
C) C
D) D
E) E

Which force is producing a counter-clockwise torque about point P?
A) A
B) B
C) C
D) D
E) E

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
20
What condition or conditions is/are necessary for static equilibrium?
A)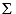 Fy = 0
Fy = 0
B) 11eea3d6_df3b_0547_97f4_6f34019e5755_TB9720_11Fx = 0, 11eea3d6_df3b_0547_97f4_6f34019e5755_TB9720_11Fy = 0
C) 11eea3d6_df3b_0547_97f4_6f34019e5755_TB9720_11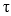 = 0
= 0
D) 11eea3d6_df3b_0547_97f4_6f34019e5755_TB9720_11Fx = 0, 11eea3d6_df3b_0547_97f4_6f34019e5755_TB9720_11Fy = 0, 11eea3d6_df3b_0547_97f4_6f34019e5755_TB9720_11 11eea3d6_b163_ca86_97f4_73bd7a12183a_TB9720_11 = 0
E) 11eea3d6_df3b_0547_97f4_6f34019e5755_TB9720_11Fx = 0
A)
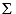 Fy = 0
Fy = 0B) 11eea3d6_df3b_0547_97f4_6f34019e5755_TB9720_11Fx = 0, 11eea3d6_df3b_0547_97f4_6f34019e5755_TB9720_11Fy = 0
C) 11eea3d6_df3b_0547_97f4_6f34019e5755_TB9720_11
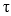 = 0
= 0D) 11eea3d6_df3b_0547_97f4_6f34019e5755_TB9720_11Fx = 0, 11eea3d6_df3b_0547_97f4_6f34019e5755_TB9720_11Fy = 0, 11eea3d6_df3b_0547_97f4_6f34019e5755_TB9720_11 11eea3d6_b163_ca86_97f4_73bd7a12183a_TB9720_11 = 0
E) 11eea3d6_df3b_0547_97f4_6f34019e5755_TB9720_11Fx = 0

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
21
A heavy seesaw is out of balance. A lightweight girl sits on the end that is tilted downward, and a heavy boy sits on the other side so that the seesaw now balances. If the boy and girl both move forward so that they are one-half their original distance from the pivot point, what will happen to the seesaw?
A) The side the boy is sitting on will now tilt downward.
B) Nothing, the seesaw will still be balanced.
C) The side the girl is sitting on will once again tilt downward.
D) It is impossible to say without knowing the masses of the children.
E) It is impossible to say without knowing the values of the original distances.
A) The side the boy is sitting on will now tilt downward.
B) Nothing, the seesaw will still be balanced.
C) The side the girl is sitting on will once again tilt downward.
D) It is impossible to say without knowing the masses of the children.
E) It is impossible to say without knowing the values of the original distances.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
22
Moment of Inertia has which of the following units?
A) kg.m2
B) N.m
C) kg.m2 / s2
D) kg.m2 / s
E) J
A) kg.m2
B) N.m
C) kg.m2 / s2
D) kg.m2 / s
E) J

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
23
Consider a solid object which is subjected to a net torque. That object will experience which of the following?
A) a linear acceleration and an angular acceleration
B) a changing moment of inertia
C) an angular acceleration
D) a constant angular velocity
A) a linear acceleration and an angular acceleration
B) a changing moment of inertia
C) an angular acceleration
D) a constant angular velocity

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
24
Consider two uniform solid spheres where both have the same diameter, but one has twice the mass of the other. The ratio of the larger moment of inertia to that of the smaller moment of inertia is
A) 8.
B) 4.
C) 6.
D) 2.
E) 10.
A) 8.
B) 4.
C) 6.
D) 2.
E) 10.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
25
A solid cylinder and a hollow cylinder have the same mass and the same radius. Which statement is true concerning their moment of inertia about an axis through the exact center of the flat surfaces?
A) The solid cylinder has the greater moment of inertia.
B) The hollow cylinder has the greater moment of inertia.
C) The moment of inertia cannot be determined since it depends on the amount of material removed from the inside of the hollow cylinder.
D) Both cylinders have the same moment of inertia.
A) The solid cylinder has the greater moment of inertia.
B) The hollow cylinder has the greater moment of inertia.
C) The moment of inertia cannot be determined since it depends on the amount of material removed from the inside of the hollow cylinder.
D) Both cylinders have the same moment of inertia.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
26
A boy and a girl are riding on a merry-go-round that is turning. The boy is twice as far as the girl from the merry-go-round's center. If the boy and girl are of equal mass, which statement is true about the boy's moment of inertia with respect to the axis of rotation?
A) The boy has a greater moment of inertia, but it is impossible to say exactly how much more.
B) His moment of inertia is twice the girl's.
C) His moment of inertia is 4 times the girl's.
D) The moment of inertia is the same for both.
E) His moment of inertia is half the girl's.
A) The boy has a greater moment of inertia, but it is impossible to say exactly how much more.
B) His moment of inertia is twice the girl's.
C) His moment of inertia is 4 times the girl's.
D) The moment of inertia is the same for both.
E) His moment of inertia is half the girl's.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
27
Rotational Kinetic Energy has which of the following units?
A) kg.m / s2
B) J
C) J.m
D) N.m2
E) kg.m2 / s
A) kg.m / s2
B) J
C) J.m
D) N.m2
E) kg.m2 / s

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
28
A ball, solid cylinder, and a hollow pipe all have equal masses and radii. If the three are released simultaneously at the top of an inclined plane, which will reach the bottom first?
A) pipe
B) cylinder
C) ball
D) they all reach bottom in the same time
A) pipe
B) cylinder
C) ball
D) they all reach bottom in the same time

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
29
Angular momentum has which of the following units?
A) J
B) kg.m2
C) N.m
D) kg.m2 / s2
E) kg. m2 / s
A) J
B) kg.m2
C) N.m
D) kg.m2 / s2
E) kg. m2 / s

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
30
Angular momentum cannot be conserved if
A) there is net torque on the system.
B) the angular velocity changes.
C) the angular displacement changes.
D) there is a net force on the system.
E) the moment of inertia changes.
A) there is net torque on the system.
B) the angular velocity changes.
C) the angular displacement changes.
D) there is a net force on the system.
E) the moment of inertia changes.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
31
A ball is attached to a string and revolves in a horizontal circle with angular momentum. When the string breaks at point B on the circumference, the ball moves off tangentially along path B-Q. As it moves along B-Q, increasing its distance from the center of the circle, its angular momentum
A) remains constant.
B) decreases.
C) is now zero.
D) increases.
A) remains constant.
B) decreases.
C) is now zero.
D) increases.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
32
An ice skater performs a pirouette (a fast spin) by pulling in his outstretched arms close to his body. What happens to his angular momentum about the axis of rotation?
A) It changes, but it is impossible to tell which way.
B) It does not change.
C) It increases.
D) It decreases.
A) It changes, but it is impossible to tell which way.
B) It does not change.
C) It increases.
D) It decreases.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
33
An ice skater performs a pirouette (a fast spin) by pulling in his outstretched arms close to his body. What happens to his moment of inertia about the axis of rotation?
A) It changes, but it is impossible to tell which way.
B) It does not change.
C) It decreases.
D) It increases.
A) It changes, but it is impossible to tell which way.
B) It does not change.
C) It decreases.
D) It increases.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
34
An ice skater performs a pirouette (a fast spin) by pulling in his outstretched arms close to his body. What happens to his rotational kinetic energy about the axis of rotation?
A) It does not change.
B) It decreases.
C) It changes, but it is impossible to tell which way.
D) It increases.
A) It does not change.
B) It decreases.
C) It changes, but it is impossible to tell which way.
D) It increases.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
35
We can best understand how a diver is able to control his rate of rotation while in the air (and thus enter the water in a vertical position) by observing that while in the air
A) his kinetic energy is constant.
B) his total energy is constant.
C) his linear momentum is constant.
D) his potential energy is constant.
E) his angular momentum is constant.
A) his kinetic energy is constant.
B) his total energy is constant.
C) his linear momentum is constant.
D) his potential energy is constant.
E) his angular momentum is constant.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
36
A planet speeds up in its orbit as it gets closer to the sun because of
A) conservation of angular momentum.
B) conservation of energy.
C) the torque exerted on the planet by the sun.
D) conservation of momentum.
E) inertia.
A) conservation of angular momentum.
B) conservation of energy.
C) the torque exerted on the planet by the sun.
D) conservation of momentum.
E) inertia.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
37
A planet of constant mass orbits the sun in an elliptical orbit. Neglecting any friction effects, what happens to the planet's rotational kinetic energy about the sun's center?
A) It increases continually.
B) It increases when the planet approaches the sun, and decreases when it moves farther away.
C) It remains constant.
D) It decreases when the planet approaches the sun, and increases when it moves farther away.
E) It decreases continually.
A) It increases continually.
B) It increases when the planet approaches the sun, and decreases when it moves farther away.
C) It remains constant.
D) It decreases when the planet approaches the sun, and increases when it moves farther away.
E) It decreases continually.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
38
Consider two equal mass cylinders rolling with the same translational velocity. The first cylinder (radius = R) is hollow and has a moment of inertia about its rotational axis of M R2, while the second cylinder (radius = r) is solid and has a moment of inertia about its axis of 0.5 M r2. What is the ratio of the hollow cylinder's angular momentum to that of the solid cylinder?
A) r to 2R
B) 2R2 to r2
C) R to 2r
D) r2 to 2R2
E) 2R to r
A) r to 2R
B) 2R2 to r2
C) R to 2r
D) r2 to 2R2
E) 2R to r

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
39
A cylinder, of radius 8.0 cm, rolls 20. cm in 5.0 s. Through what angular displacement does the cylinder move in this time?

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
40
A 50. cm diameter wheel is rotating initially at 2.0 revolutions per second. It slows down uniformly and comes to rest in 15. seconds.
(a) What was its angular acceleration?
(b) Through how many revolutions did it turn in those 15. s?
(a) What was its angular acceleration?
(b) Through how many revolutions did it turn in those 15. s?

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
41
A wheel slows down uniformly and comes to rest in 15. seconds. It is rotating initially at 2.0 revolutions per second and has a diameter of 50.cm.
(a) What was the centripetal acceleration at the instant when it was rotating initially?
(b) What was the tangential acceleration?
(a) What was the centripetal acceleration at the instant when it was rotating initially?
(b) What was the tangential acceleration?

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
42
A wheel of diameter 0.70 m rolls without slipping. A point at the top of the wheel moves with a tangential speed 2.0 m/s.
(a) At what speed is the axis of the wheel moving?
(b) What is the angular speed of the wheel?
(a) At what speed is the axis of the wheel moving?
(b) What is the angular speed of the wheel?

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
43
A majorette fastens two batons together at their centers to form an X shape. What is the moment of inertia of the combination about an axis through the center of the X if each baton was 1.2 m long and each ball at the end of each baton has a mass of 0.25 kg (assume negligible mass in the rods)?

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
44
A triatomic molecule is modeled as follows: mass m is at the origin, mass 2m is at x = a, and mass 3m is at x = 2a.
(a) What is the amount of inertia about the origin?
(b) What is the moment of inertia about the center of mass?
(a) What is the amount of inertia about the origin?
(b) What is the moment of inertia about the center of mass?

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
45
A 2.50 kg is at ( 1.00, 3.00) meters. What is the moment of inertia:
(a) about the x-axis?
(b) about the y-axis?
(c) about the line defined by x= 6.00 m?
(a) about the x-axis?
(b) about the y-axis?
(c) about the line defined by x= 6.00 m?

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
46
A cylinder of radius R and mass M rolls without slipping down a plane inclined at an angle θ above horizontal.
(a) What is the torque about the point of contact with the plane?
(b) What is the moment of inertia about the point of contact?
(c) What is the linear speed of the cylinder t seconds after it is released from rest?
(a) What is the torque about the point of contact with the plane?
(b) What is the moment of inertia about the point of contact?
(c) What is the linear speed of the cylinder t seconds after it is released from rest?

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
47
Consider a bus designed to obtain its motive power from a large rotating flywheel (1400. kg of diameter 1.5 m) that is periodically brought up to its maximum speed of 3600. rpm by an electric motor at the terminal. If the bus requires an average power of 12. kilowatts, how long will it operate between recharges?

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
48
Consider a motorcycle of mass 150. kg, one wheel of which has a mass of 10. kg and a radius of 30. cm. What is the ratio of the rotational kinetic energy of the wheels to the total translational kinetic energy of the bike? Assume the wheels are uniform disks.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
49
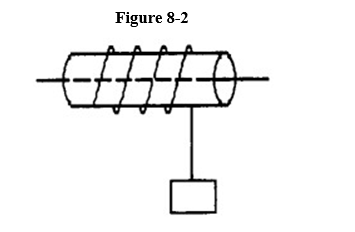
A uniform solid cylinder (mass 100. kg and radius 50.0 cm) is mounted so it is free to rotate about fixed horizontal axis that passes through the centers of its circular ends. A 10.0 kg block is hung from a massless cord wrapped around the cylinder's circumference. When the block is released, the cord unwinds and the block accelerates downward, as shown in Figure 8-2. What is the block's acceleration?


Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
50
Two children, each of mass 20.0 kg, ride on the perimeter of a small merry-go-round that is rotating at the rate of 1.0 revolution every 4.0 s. The merry-go-round is a disk of mass 30. kg and radius 3.0 m. The children now both move halfway in toward the center to positions 1.5 m from the axis of rotation. Calculate the kinetic energy before and after, and the final rate of rotation. Explain any changes in energy.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
51
A ballerina spins initially at 1.5 revolutions/second when her arms are extended. She then draws in her arms to her body and her moment of inertia becomes 0.88 kg-m2 and her angular speed increases to 4.0 rev/s. Determine her initial moment of inertia.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
52
A solid disk with diameter 2.00 meters and mass 4.0 kg freely rotates about a vertical axis at 36. rpm. A 0.50 kg hunk of bubblegum is dropped onto the disk and sticks to the disk at a distance d = 80. cm from the axis of rotation, as shown in Figure 8-3.
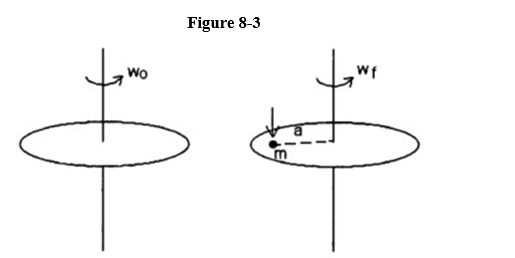
(a) What was the moment of inertia before the gum fell?
(b) What was the moment of inertia after the gum stuck?
(c) What is the angular velocity after the gum fell onto the disk?

(a) What was the moment of inertia before the gum fell?
(b) What was the moment of inertia after the gum stuck?
(c) What is the angular velocity after the gum fell onto the disk?

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
53
NASA puts a satellite in space which consists of two (32. kg each) masses connected by a 12. meter long light cable, as shown in Figure 8-4. The entire system initially is rotating 4.0 rpm about an axis (at the center of mass) perpendicular to the cable. Motors in each mass reel out more cable so that the masses double their separation (to 24. m).

(a) What is the final ROTATIONAL VELOCITY?
(b) The final KINETIC ENERGY is what fraction of the initial?

(a) What is the final ROTATIONAL VELOCITY?
(b) The final KINETIC ENERGY is what fraction of the initial?

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
54
A bicycle is moving 4.0 m/s. What is the angular speed of a wheel if its radius is 30.cm?
A) 1.2 rad/s
B) 4.8 rad/s
C) 0.36 rad/s
D) 13. rad/s
E) 7.6 rad/s
A) 1.2 rad/s
B) 4.8 rad/s
C) 0.36 rad/s
D) 13. rad/s
E) 7.6 rad/s

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
55
A uniform rod has a weight of 40. N and a length of 1.0 m. It is hinged to a wall (at the left end) , and held in a horizontal position by a vertical massless string (at the right end), as shown in 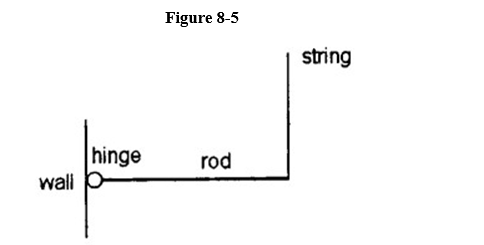
What is the magnitude of the torque exerted by the string about a horizontal axis which passes through the hinge and is perpendicular to the rod?
A) 40 m . N
B) 5.0 m . N
C) 30 m . N
D) 20 m . N
E) 10 m . N

What is the magnitude of the torque exerted by the string about a horizontal axis which passes through the hinge and is perpendicular to the rod?
A) 40 m . N
B) 5.0 m . N
C) 30 m . N
D) 20 m . N
E) 10 m . N

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
56
A force is applied to the end of a 2.0 ft long uniform board weighing 50. lb, in order to keep it horizontal, while it pushes against a wall at the left. If the angle the force makes with the board is 30° in the direction shown in Figure 8-6, what is the applied force F?

A) 29. lb
B) 58. lb
C) 32. lb
D) 50. lb
E) 90. lb

A) 29. lb
B) 58. lb
C) 32. lb
D) 50. lb
E) 90. lb

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
57
A boy and a girl are balanced on a massless seesaw. The boy has a mass of 60 kg and the girl's mass is 50 kg. If the boy sits 1.5 m from the pivot point on one side of the seesaw, where must the girl sit on the other side for equilibrium?
A) 3.0 m
B) 1.8 m
C) 1.2 m
D) 1.3 m
E) 2.5 m
A) 3.0 m
B) 1.8 m
C) 1.2 m
D) 1.3 m
E) 2.5 m

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
58
Consider two uniform solid spheres where one has twice the mass and twice the diameter of the other. The ratio of the larger moment of inertia to that of the smaller moment of inertia is
A) 10.
B) 8.
C) 2.
D) 4.
E) 6.
A) 10.
B) 8.
C) 2.
D) 4.
E) 6.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
59
A 4.0 kg mass is hung from a string which is wrapped around a cylindrical pulley (a cylindrical shell) Figure 8-7
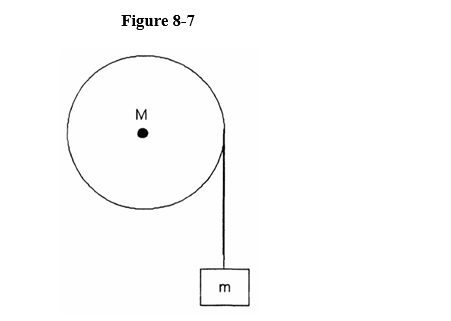
If the mass accelerates downward at 4.90 m/s2, what is the mass of the pulley?
A) 4.0 kg
B) 2.0 kg
C) 6.0 kg
D) 8.0 kg
E) 10.0 kg

If the mass accelerates downward at 4.90 m/s2, what is the mass of the pulley?
A) 4.0 kg
B) 2.0 kg
C) 6.0 kg
D) 8.0 kg
E) 10.0 kg

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
60
A uniform rod has a length of 2.0 m. It is hinged to a wall (at the left end) , and held in a horizontal position by a vertical massless string (at the right end), as shown in Figure 8-8
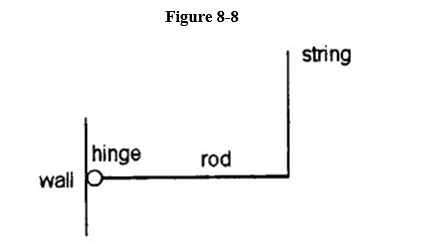
What is the angular acceleration of the rod at the moment the string is released?
A) 15. rad/s2
B) It can't be calculated without knowing the rod's mass.
C) 3.3 rad/s2
D) 7.4 rad/s2
E) 11. rad/s2

What is the angular acceleration of the rod at the moment the string is released?
A) 15. rad/s2
B) It can't be calculated without knowing the rod's mass.
C) 3.3 rad/s2
D) 7.4 rad/s2
E) 11. rad/s2

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
61
A potter's wheel with a moment of inertia of 8.0 kg-m2 has 5.0 N-m applied to it. It starts from rest. 10. s later it has gained what kinetic energy?
A) 44. J
B) 78. J
C) 1.6 kJ
D) 0.12 kJ
E) 53. J
A) 44. J
B) 78. J
C) 1.6 kJ
D) 0.12 kJ
E) 53. J

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
62
A wheel of moment of inertia of 5.00 kg-m2 starts from rest and accelerates under a constant torque of 3.00 N-m for 8.00 s. What is the wheel's rotational kinetic energy at the end of 8.00 s?
A) 57.6 J
B) 64.0 J
C) 91.9 J
D) 122.0 J
E) 78.8 J
A) 57.6 J
B) 64.0 J
C) 91.9 J
D) 122.0 J
E) 78.8 J

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
63
The moment of inertia of a solid cylinder about its axis is given by 0.5MR2. If this cylinder rolls without slipping, the ratio of its rotational kinetic energy to its translational kinetic energy is
A) 1:2
B) 2:1
C) 1:1
D) 1:3
E) 3:1
A) 1:2
B) 2:1
C) 1:1
D) 1:3
E) 3:1

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
64
A hoop of radius 0.50 m and a mass of 0.20 kg is released from rest and allowed to roll down an inclined plane. How fast is it moving after dropping a vertical distance of 3.0 m?
A) 7.7 m/s
B) 3.8 m/s
C) 2.2 m/s
D) 6.2 m/s
E) 5.4 m/s
A) 7.7 m/s
B) 3.8 m/s
C) 2.2 m/s
D) 6.2 m/s
E) 5.4 m/s

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
65
An 8.0 kg-m2 wheel with 155. Joules of rotational kinetic energy requires what torque to bring it to rest in 4.0 s?
A) -1.2 N-m
B) -1.8 N-m
C) -1.0 N-m
D) -1.6 N-m
E) +0.88 N-m
A) -1.2 N-m
B) -1.8 N-m
C) -1.0 N-m
D) -1.6 N-m
E) +0.88 N-m

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
66
A proton of mass M rotates with an angular speed of 2 × 106 rad/s in a circle of radius 0.80 m in a cyclotron. What is the orbital angular momentum of the proton? (M = 1.67 × 10-27 kg)
A) 2.1 × 10-21 N-m-s
B) 5.3 × 10-21 N-m-s
C) 3.9 × 10-21 N-m-s
D) 2.9 × 10-21 N-m-s
E) 1.1 × 10-20 N-m-s
A) 2.1 × 10-21 N-m-s
B) 5.3 × 10-21 N-m-s
C) 3.9 × 10-21 N-m-s
D) 2.9 × 10-21 N-m-s
E) 1.1 × 10-20 N-m-s

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
67
Initially, a 2.00-kg mass is whirling at the end of a string (in a circular path of radius 0.750 m) Figure 8-9 The string has been slowly winding around a vertical rod, and a few seconds later the length of the string has shortened to 0.250 m.
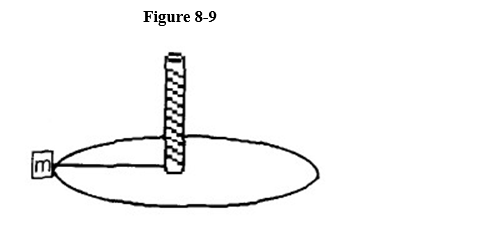
What is the instantaneous speed of the mass at the moment the string reaches a length of 0.250 m?
A) 3.9 m/s
B) 9.3 m/s
C) 15 m/s
D) 225 m/s
E) 75 m/s

What is the instantaneous speed of the mass at the moment the string reaches a length of 0.250 m?
A) 3.9 m/s
B) 9.3 m/s
C) 15 m/s
D) 225 m/s
E) 75 m/s

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
68
An object's angular momentum changes by 10 kg-m2/s in 2.0 s. What magnitude average torque acted on this object?
A) 10 N-m
B) 5 N-m
C) 2.5 N-m
D) 40 N-m
E) 20 N-m
A) 10 N-m
B) 5 N-m
C) 2.5 N-m
D) 40 N-m
E) 20 N-m

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck



