Deck 18: Electric Current and Circuits
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/36
Play
Full screen (f)
Deck 18: Electric Current and Circuits
1
A current is carried by a copper wire of radius . If the density of conduction electrons is , what is the drift velocity of the conduction electrons?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
2
Silver contains conduction electrons per . How many conduction electrons are in a length of silver wire of diameter ?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
3
Aluminum has a resistivity of . What is the resistance of of aluminum wire with cross-sectional area ?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
4
One hundred meters of a certain type of wire has a resistance of . What is the resistance of of this wire?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 36 flashcards in this deck.
Unlock Deck
k this deck
5
One hundred meters of diameter wire has a resistance of . What is the resistivity of the material from which the wire is made?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 36 flashcards in this deck.
Unlock Deck
k this deck
6
The resistance of a wire increases by when the temperature of the wire is raised . What is the temperature coefficient of resistivity of the wire material?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 36 flashcards in this deck.
Unlock Deck
k this deck
7
A battery has an internal resistance of . What is the maximum current that can be drawn from this battery?
A)
B)
C) infinite (or at least 1000s of amps)
D)
E)
A)
B)
C) infinite (or at least 1000s of amps)
D)
E)

Unlock Deck
Unlock for access to all 36 flashcards in this deck.
Unlock Deck
k this deck
8
The potential difference of is placed across a resistor. What is the current in the resistor?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 36 flashcards in this deck.
Unlock Deck
k this deck
9
A battery is connected across a resistor. If the current through the resistor is , what is the terminal voltage of the battery?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 36 flashcards in this deck.
Unlock Deck
k this deck
10
A battery has an internal resistance of . If the battery supplies when connected to a starter motor, what is the resistance of the motor?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 36 flashcards in this deck.
Unlock Deck
k this deck
11
The potential differences around a loop in a circuit (starting at and going around the loop back to A) are , and . What is ?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 36 flashcards in this deck.
Unlock Deck
k this deck
12
A resistor and a resistor are connected in parallel to a battery of negligible internal resistance. What is the current in the resistor?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 36 flashcards in this deck.
Unlock Deck
k this deck
13
What is the resistance of this combination of resistors?
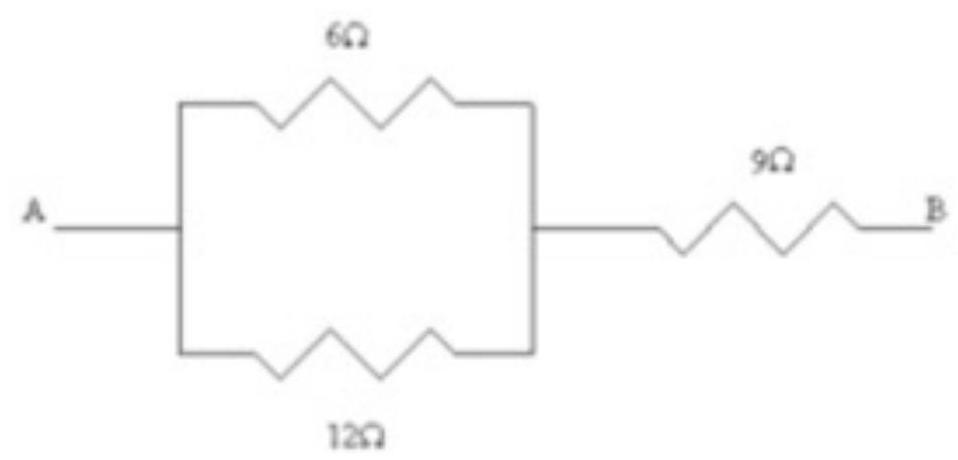
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 36 flashcards in this deck.
Unlock Deck
k this deck
14
Two capacitors of values and are connected in series. What is the capacitance of the combination?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 36 flashcards in this deck.
Unlock Deck
k this deck
15
Two capacitors of values and are connected in series to a power supply. What is the resulting charge on the capacitor?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 36 flashcards in this deck.
Unlock Deck
k this deck
16
Capacitors of values , and are connected in series across a power supply. Which capacitor has the greatest potential difference across it?
A) the capacitor
B) the capacitor
C) the capacitor
D) the capacitor
E) they all are equal
A) the capacitor
B) the capacitor
C) the capacitor
D) the capacitor
E) they all are equal

Unlock Deck
Unlock for access to all 36 flashcards in this deck.
Unlock Deck
k this deck
17
Capacitors of values , and are connected in series across a power supply. Which capacitor has the greatest charge on it?
A) the capacitor
B) the capacitor
C) the capacitor
D) the capacitor
E) they are all equal
A) the capacitor
B) the capacitor
C) the capacitor
D) the capacitor
E) they are all equal

Unlock Deck
Unlock for access to all 36 flashcards in this deck.
Unlock Deck
k this deck
18
The arrangement shown is composed of four capacitors. What is the capacitance of the combination?
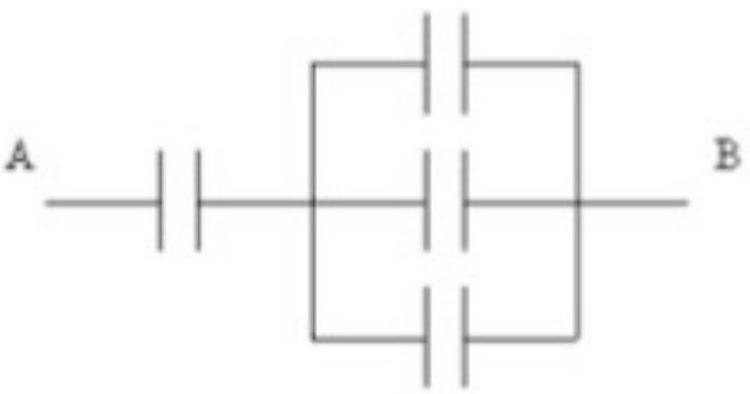
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 36 flashcards in this deck.
Unlock Deck
k this deck
19
If , and , what is the current in ?
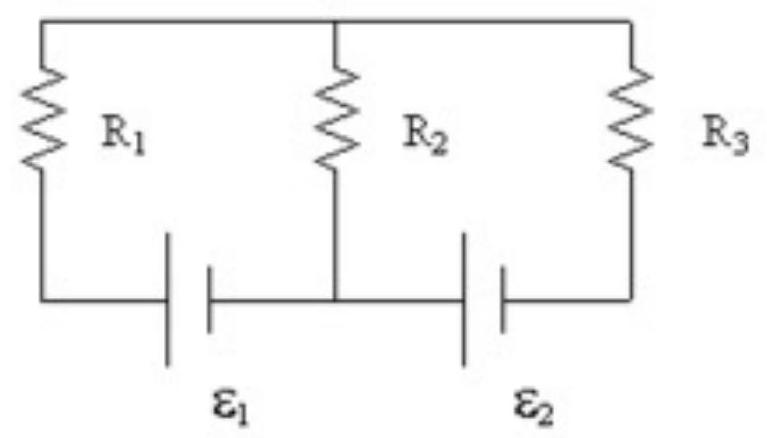
A) 1 A down
B) up
C) 2.5 A down
D) 5 A down
E) up

A) 1 A down
B) up
C) 2.5 A down
D) 5 A down
E) up

Unlock Deck
Unlock for access to all 36 flashcards in this deck.
Unlock Deck
k this deck
20
If , and , what is the power supplied to the circuit by ?
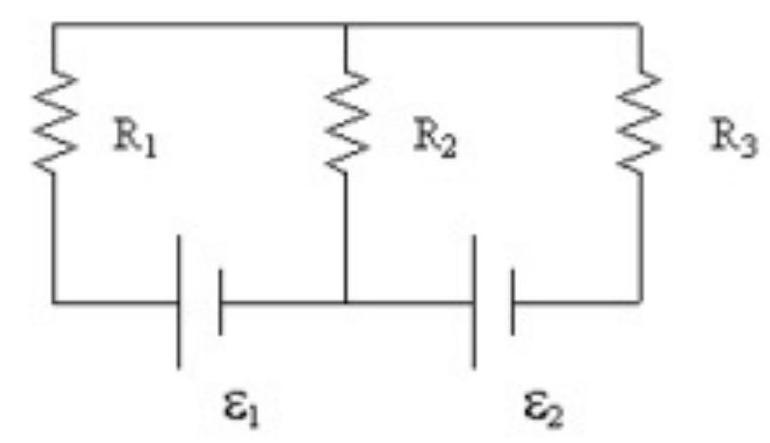
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 36 flashcards in this deck.
Unlock Deck
k this deck
21
Three resistors, , and , are connected in series to a battery. What is the total power dissipated by the circuit?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 36 flashcards in this deck.
Unlock Deck
k this deck
22
Three resistors, , and , are connected in series to a battery. What is the power dissipated by ?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 36 flashcards in this deck.
Unlock Deck
k this deck
23
Three resistors, , and , are connected in parallel to a battery. What is the power dissipated by ?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 36 flashcards in this deck.
Unlock Deck
k this deck
24
Three resistors, , and , are connected in parallel to a battery. What is the total power dissipated in the circuit?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 36 flashcards in this deck.
Unlock Deck
k this deck
25
The watt, , is equivalent to which of the following?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 36 flashcards in this deck.
Unlock Deck
k this deck
26
A resistor is connected across a power supply. An ammeter with internal resistance of is used to measure the current in this circuit. What is the ammeter reading?
A)
B)
C)
D)
E) an ammeter with less resistance than the rest of the circuit will not produce a reading
A)
B)
C)
D)
E) an ammeter with less resistance than the rest of the circuit will not produce a reading

Unlock Deck
Unlock for access to all 36 flashcards in this deck.
Unlock Deck
k this deck
27
A series circuit consists of a source of emf, a capacitor, a resistor, and a switch. What is the time constant for this circuit?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 36 flashcards in this deck.
Unlock Deck
k this deck
28
Copper has current-carrying electrons per . A copper wire of radius carries a current of . What is the average drift velocity for the electrons?
A)
B)
C)
D) more information is needed for this calculation
A)
B)
C)
D) more information is needed for this calculation

Unlock Deck
Unlock for access to all 36 flashcards in this deck.
Unlock Deck
k this deck
29
A wire of radius is made of an unknown metal and carries a current of . The drift velocity for electrons in the wire is measured to be . What is the charge carrier density of the metal from which the wire is made?
A)
B)
C)
D) need more information to do this calculation.
A)
B)
C)
D) need more information to do this calculation.

Unlock Deck
Unlock for access to all 36 flashcards in this deck.
Unlock Deck
k this deck
30
Copper has current carrying electrons per . A copper wire carries a current of , and the drift velocity of the electrons is measured to be . What is the wire's radius?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 36 flashcards in this deck.
Unlock Deck
k this deck
31
A carbon resistor is made of a cylinder of carbon, of length . If the resistivity of carbon is , and a potential difference of causes a current of to flow through the resistor, what is the radius of the cylinder?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 36 flashcards in this deck.
Unlock Deck
k this deck
32
A carbon resistor is made of a cylinder of carbon, of diameter . If the resistivity of carbon is , and a potential difference of causes a current of to flow through the resistor, what is the length of the cylinder?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 36 flashcards in this deck.
Unlock Deck
k this deck
33
A circuit joins points and into a single square loop. The voltage drops from to to , and to , are , and , respectively. If one were to measure the voltage drop from to , one would obtain:
A)
B)
C)
D)
E)
F)
A)
B)
C)
D)
E)
F)

Unlock Deck
Unlock for access to all 36 flashcards in this deck.
Unlock Deck
k this deck
34
Two identical circuits have a capacitor in series with a resistor and a switch. In circuit , the resistor has resistance , while in circuit , its resistance is . The capacitors are identical. Each capacitor begins fully charged, and each circuit is open. When each circuit is completed (i.e., the switch in them is closed), the capacitor will begin to discharge. If a time is required for circuit A's capacitor to fully discharge (say, by ), what time will be required for circuit B's capacitor to do the same?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 36 flashcards in this deck.
Unlock Deck
k this deck
35
What is the ratio of the time it takes for the capacitor in a series RC circuit to reach of maximum charge from an uncharged state, to the time required for the capacitor to discharge from a fully charged state to ?
A) Answer depends on the particular values of and .
B) 9 times as long
C) The same time is required.
D) as long
E) 22 times as long
F) times as long
A) Answer depends on the particular values of and .
B) 9 times as long
C) The same time is required.
D) as long
E) 22 times as long
F) times as long

Unlock Deck
Unlock for access to all 36 flashcards in this deck.
Unlock Deck
k this deck
36
Two ceramic cylinders have the following properties. Cylinder has radius and height , while Cylinder has radius and height . Their resistances are measured, and it is found that . What is the ratio of the resistivities of the ceramics from which the cylinders are made?
A)
B)
C)
D)
E) 36
F)
A)
B)
C)
D)
E) 36
F)

Unlock Deck
Unlock for access to all 36 flashcards in this deck.
Unlock Deck
k this deck



