Question 1

Contiguous states often use tax policy to attract residents, firms, and economic activity. These ?tax competitions? between states can be modeled with game theory. Suppose New Jersey currently has a state sales tax of 7 percent and Pennsylvania has a state sales tax of 6 percent. The game shown below models the effect of a reduction in each state?s sales tax rate to 3 percent on each state?s sales tax revenue. Assume the motivation of each state is to maximize tax revenue. The first number in a cell is the payoff to New Jersey; the second number is the payoff to Pennsylvania.

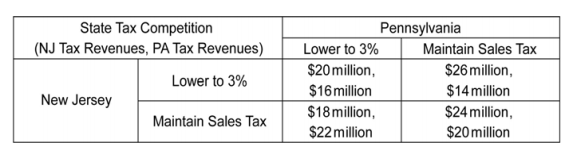
-Refer to the scenario above. Is there a set of payoffs that is superior to the payoffs realized at the dominant strategy equilibrium?

A) No.
B) Yes, New Jersey maintains its sales tax rate, realizing $18 million in tax revenues, and Pennsylvania lowers its sales tax rate, realizing $22 million in tax revenues.
C) Yes, New Jersey maintains its sales tax rate, realizing $24 million in tax revenues, and Pennsylvania also maintains its sales tax rate, realizing $20 million in tax revenues.
D) Yes, New Jersey lowers its sales tax rate, realizing $26 million in tax revenues, and Pennsylvania maintains its sales tax rate, realizing $14 million in tax revenues.

Yes, New Jersey maintains its sales tax rate, realizing $24 million in tax revenues, and Pennsylvania also maintains its sales tax rate, realizing $20 million in tax revenues.

Accepted Answer

In game theory, a dominant strategy equilibrium may not always lead to the best overall outcome for all players involved. The scenario described in option C suggests a cooperative outcome where both New Jersey and Pennsylvania maintain their sales tax rates, leading to a higher combined revenue ($24 million + $20 million = $44 million) compared to the outcomes where one or both states lower their tax rates. This indicates that there is indeed a set of payoffs superior to those realized at the dominant strategy equilibrium, showcasing the potential benefits of cooperation over competition in certain strategic scenarios.

Question 2

Consider another version of the advertising game between Mountain Dew and Mello Yello. Again, each brand is deciding whether to launch an advertising campaign. These decisions will be taken simultaneously, the brands will not be cooperating, and we will assume each brand's strategist knows her own and her opponent's payoffs in all cases. The payoff matrix is listed below.
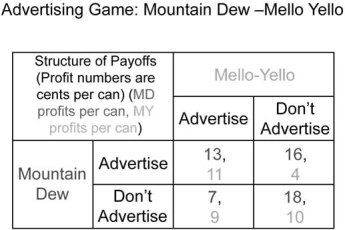Is there a Nash equilibrium in this advertising game?

A) Yes, Mountain Dew chooses to not advertise, Mello Yello chooses to advertise
B) Yes, both Mountain Dew and Mello Yello choose to advertise
C) Yes, both Mountain Dew and Mello Yello choose to not advertise
D) Yes, both (B and C)

Yes, both (B and C)

Accepted Answer

Yes, both (B and C)&#10;

Question 3

Vladimir and Alphonso are collectors of Toy Story figurines. Each has six dollar bills to spend on three figurines-Sheriff Woody, Buzz Lightyear, and Jessie-that are put up for auction where Vlad and Alph are the only bidders. They simultaneously and independently write down their bids, in whole numbers adding up to $6, for the three figurines and give them to the auctioneer. Whoever wrote the higher number for a figurine wins it. For example, if Vlad bids ($3, $1, $2), meaning $3 for Sheriff Woody, $1 for Buzz Lightyear, and $2 for Jessie, and Alph bids ($2, $3, $1), then Vlad wins Sheriff Woody and Jessie, while Alph wins Buzz Lightyear. If there is a tie, then a fair coin is flipped to determine the winner so that each bidder has 50 percent chance of winning a figurine. Vlad and Alph consider this case as ?winning? a (1/2)figurine. Vlad and Alph care only about how many more, or less, figurines they win compared to the other.

-Refer to the scenario above. This game is an example of ________.

A) the prisoners? dilemma
B) a non-zero-sum game
C) a zero-sum game
D) the tragedy of commons

a zero-sum game

Accepted Answer

In this scenario, the game is a zero-sum game because the gain or loss of a figurine by one player directly corresponds to the loss or gain of the other player. The total number of figurines won by both players combined remains constant, meaning that one player's win is exactly equal to the other player's loss.

Question 4

Another game frequently played in MBA strategy classes is the acquire a company game. The set-up of the game is as follows. Company A has only one asset, offshore oil leases. The expected profit from these leases is uniformly distributed between $0 and $100 million, so the expected value to company A is $50 million. Company B is thinking of acquiring Company A. Company B's management is more efficient than A's; specifically, the value of A's assets under B's management is 1.5 times greater. For example, the expected value of A's oil leases under B's management is 1.5 $50 million, or $75 million. Company B can submit a written bid to acquire Company A. A will review the bid, and accept or reject the offer after learning the value of the oil leases with certainty.
You are advising Company B on its potential acquisition of Company A. What is the optimal bid for Company B to submit?

A) Do not submit a bid
B) Bid $50 million
C) Bid $75 million
D) Bid $100 million

Accepted Answer

The optimal bid is to not bid at all. Any bid accepted by Company A is always weakly greater than the value of the oil leases, because Company A knows with certainty the value of the oil leases when it reviews Company B's offer. The most common bid submitted in classroom experiments is $75 million, which is just 1.5 times Company A's expected value of the oil leases ($50 million). But Company A will only accept B's bid of $75 million when the oil leases are worth $75 million or less; it will reject B's bid of $75 million when the oil leases are worth more than $75 million.

Question 5

Suppose two outdoor apparel firms, L.L. Bean and Eddie Bauer, are contemplating introducing the same new product to their existing product lines. For this problem, assume that Eddie Bauer "moves" (makes this decision) first, and then L.L. Bean makes its decision. Each firm can choose to either introduce the new product or continue with the existing product. Eddie Bauer moves first, and there is "full information," meaning that each firm knows the potential payoffs (profits associated with each action). In the extensive form of this sequential game, shown in the figure below, profits (shown in parentheses in the art) are annual profits in thousands of dollars.
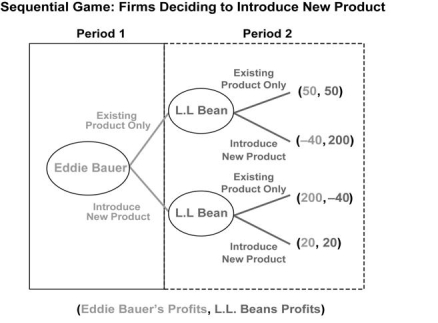Given the information above, which of the following statements is true? Explain how you arrived at your answer.

A) Eddie Bauer should always choose to maintain the existing product only.
B) L.L. Bean should choose to introduce the new product if Eddie Bauer chooses to introduce the new product.
C) L.L. Bean should choose to maintain the existing product only if Eddie Bauer chooses to maintain the existing product.
D) L.L. Bean should choose to maintain the existing product only if Eddie Bauer chooses to introduce the new product.

Accepted Answer

We solve these types of problems by working backward, a technique called backward induction. Essentially, Eddie Bauer can figure out what L.L. Bean will do in period 2 based on its own (Eddie Bauer?s) strategy in period 2, because each firm has complete information (e.g., Eddie Bauer knows the payoffs L.L. Bean will receive by following each strategy). So, Eddie Bauer asks itself, if we maintain the existing product, what will L.L. Bean's best response be' L.L. Bean earns profits of 200 if it chooses to introduce a new product, but only 50 if it maintains the existing product only. So L.L. Bean's best response to Eddie Bauer?s decision to maintain the existing product only is to introduce a new product. Knowing L.L. Bean's best response, Eddie Bauer can see that its profits in Period 2 will be -40 if it chooses to maintain the existing product only.
If Eddie Bauer chooses to introduce a new product, L.L. Bean will incur a loss of 40 if it also maintains the existing product only, or a profit of 20 if it also introduces a new product. So, L.L. Bean's best response to Eddie Bauer's introduction of a new product is to also introduce a new product. If L.L. Bean pursues a strategy of introducing a new product in period 2 in response to Eddie Bauer's introduction of a new product in period 1, Eddie Bauer will earn profits of 20 in period 2.
So by solving this game backward, Eddie Bauer realizes it will incur a loss of 40 by choosing to maintain the existing product only, or a profit of 20 if it chooses to introduce a new product. Since we assume firms are profit maximizers, Eddie Bauer's optimal period 1 strategy is to introduce a new product, because this strategy maximizes period 2 profits, given L.L. Bean's best response in period 2.

Question 6

Bill and Tom are playing a game. At each round of the game, they have to choose either Strategy X or Strategy Y. However, Tom can make a decision only after Bill has made his decision. If they both choose X, each gains $100, and if both of them choose Y, each gains $50. However, if Bill chooses X and Tom chooses Y, Bill gains $60 while Tom gains $140. Similarly, when Bill chooses Y and Tom chooses X, Tom gains $60 while Bill gains $140.
a) Draw a game tree to represent this game.
b) What type of game is being played? What is the procedure used to solve such a game?
c) What is Tom?s optimal strategy if Bill chooses Strategy X?
d) What is Bill?s payoff in equilibrium?

Accepted Answer

The answer of Bill and Tom are playing a game....

Question 7

Two rival cosmetics brands are considering launching a new product. If Firm 1 launches a product for older women while Firm 2 targets college students, Firm 1 will earn $40,000, while Firm 2 will earn $50,000. If both the firms launch a product for older women, Firm 1 will earn $20,000, while Firm 2 will earn $15,000. If Firm 1 launches a product for college students while Firm 2 targets older women, Firm 1 will earn $60,000, while Firm 2 will earn $40,000. If both firms target college students, both firms will earn $30,000. However, Firm 2 will choose its target consumers after Firm 1 has chosen its target consumers.
a) Draw a game tree to represent this situation.
b) What is the equilibrium outcome of this game?
c) Will there be a change in the equilibrium outcome if the firms make decisions simultaneously?

Accepted Answer

The answer of Two rival cosmetics brands are considering launching...

Question 8

Recall the trust game reported in the Evidence-Based Economics element in section 13.5. Consider the game where the trust game is played twice in succession.

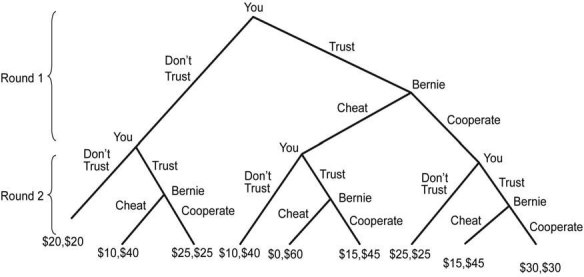Payoffs are the sum of payoff in each round. For example, suppose you choose Trust and Bernie chooses Cheat in the first round, then you choose Don?t Trust in the second round (Bernie could choose either, because it does not get to his turn anyway). Then you earn $0 and Bernie earns $30 in the first round, and you earn $10 and Bernie earns $10 in the second round, so that your total payoff is $10 and Bernie?s is $40.
a) Apply backward induction to this game. How do you and Bernie behave in the two-round version?
b) What would be the backward induction solution if the trust game is repeated three times? Four times? Twenty thousand times? Does this agree with what you read in the Evidence-Based Economics element in section 13.5?

Accepted Answer

The answer of Recall the trust game reported in the...

Deck 11: Game Theory and Strategic Play