Deck 6: Some Rules of Probability

Question 1

The expression $P(A \cap B)=P(A) P(B \mid A)$ is valid if

A) $A$ and $B$ are independent.
B) $A$ and $B$ are mutually exclusive.
C) only if $A$ equals $B^{\prime}$ .
D) for any events $A$ and $B$ .

Answer 1

for any events $A$ and $B$ .

Question 2

If $A$ and $B$ are independent events, with $P(A)=\frac{1}{5}, P(B)=\frac{2}{5}$ , then $P(A \cup B)$

A) equals $\frac{3}{5}$ .
B) equals $\frac{13}{25}$ .
C) equals $\frac{3}{25}$ .
D) cannot be determined from the given information.

Answer 2

equals $\frac{13}{25}$ .

Question 3

If the odds in favor of an event occurring is 9 to 2 , then the probability that the event will not occur is

A) $\frac{2}{11}$ .
B) $\frac{9}{11}$ .
C) $\frac{2}{9}$ .
D) $\frac{9}{2}$ .

Answer 3

$\frac{2}{11}$ .

Question 4

The expression $P(A \cup B)=P(A)+P(B)$ is valid if

A) $A$ and $B$ are independent.
B) $A$ and $B$ are mutually exclusive.
C) $A$ and $B$ are dependent.
D) none of these.

Question 5

If $A$ and $B$ are mutually exclusive events with $P(A)=\frac{1}{7}, P(B)=\frac{2}{7}$ , then $P(A \cup B)$ equals

A) $\frac{3}{7}$ .
B) $\frac{19}{49}$ .
C) $\frac{2}{47}$ .
D) 0 .

Question 6

Which of the following may be true if $A$ and $B$ are dependent events?

A) $P(A \cup B)>1$
B) $P(A)+P(B)>1$
C) $P(A \cap B)<0$
D) $P(A \mid B)=P(A)$

Question 7

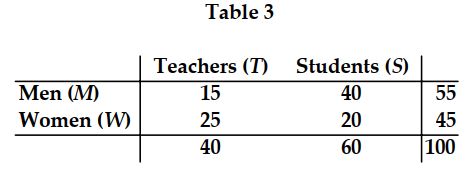
-Use the data in Table 3 to solve the following: The probability expressed by $P(S \cup W)$ equals

A) $\frac{85}{100}$ .
B) $\frac{20}{100}$ .
C) $\frac{20}{45}$ .
D) $\frac{40}{60}$ .

Question 8

-Using Table 3, the probability that a person is a woman, given that the person is not a teacher is

A) $\frac{20}{100}$ .
B) $\frac{25}{40}$ .
C) $\frac{20}{60}$ .
D) $\frac{25}{100}$ .

Question 9

Two probabilities may be added when we are asked

A) an "or" question and the events are independent.
B) an "or" question and the events are mutually exclusive.
C) an "and" question and the events are independent.
D) an "and" question and the events are mutually exclusive.

Question 10

Two probabilities may be multiplied when we are asked

A) an "or" question and the events are independent.
B) an "or" question and the events are mutually exclusive.
C) an "and" question and the events are independent.
D) an "and" question and the events are mutually exclusive.

Question 11

In an experiment, persons are asked to pick a number from 10 to 18 , so that for each person the sample space is the set $S=\{10,11,12,13,14,15,16,17,18\}$ . If $A=\{10,11,15,16,17\}, B=\{10,12,14\}$ , and $C=\{14,16,18\}$ , list the elements of the sample space comprising each of the following events.
- $A^{\prime}$

Question 12

In an experiment, persons are asked to pick a number from 10 to 18 , so that for each person the sample space is the set $S=\{10,11,12,13,14,15,16,17,18\}$ . If $A=\{10,11,15,16,17\}, B=\{10,12,14\}$ , and $C=\{14,16,18\}$ , list the elements of the sample space comprising each of the following events.
- $B \cup C$

Question 13

In an experiment, persons are asked to pick a number from 10 to 18 , so that for each person the sample space is the set $S=\{10,11,12,13,14,15,16,17,18\}$ . If $A=\{10,11,15,16,17\}, B=\{10,12,14\}$ , and $C=\{14,16,18\}$ , list the elements of the sample space comprising each of the following events.
- $A \cap C$

Question 14

In an experiment, persons are asked to pick a number from 10 to 18 , so that for each person the sample space is the set $S=\{10,11,12,13,14,15,16,17,18\}$ . If $A=\{10,11,15,16,17\}, B=\{10,12,14\}$ , and $C=\{14,16,18\}$ , list the elements of the sample space comprising each of the following events.
- $A^{\prime} \cap B$

Question 15

A company has discovered a way of evaluating the success of both their radio and television advertising. If $R$ and $T$ are, respectively, the events that the radio advertising and television advertising are successful, $P(R)=0.62, P(T)=0.75$ , and $P(R \cap T)=\mathbf{0 . 4 3}$ .
-Using the situation above, solve the following: $P\left(R^{\prime}\right)$ .

Question 16

A company has discovered a way of evaluating the success of both their radio and television advertising. If $R$ and $T$ are, respectively, the events that the radio advertising and television advertising are successful, $P(R)=0.62, P(T)=0.75$ , and $P(R \cap T)=\mathbf{0 . 4 3}$ .
-Using the situation above, solve the following: $P(R \cup T)$ .

Question 17

A company has discovered a way of evaluating the success of both their radio and television advertising. If $R$ and $T$ are, respectively, the events that the radio advertising and television advertising are successful, $P(R)=0.62, P(T)=0.75$ , and $P(R \cap T)=\mathbf{0 . 4 3}$ .
-Using the situation above, solve the following: $P\left(R \cap T^{\prime}\right)$ .

Question 18

A company has discovered a way of evaluating the success of both their radio and television advertising. If $R$ and $T$ are, respectively, the events that the radio advertising and television advertising are successful, $P(R)=0.62, P(T)=0.75$ , and $P(R \cap T)=\mathbf{0 . 4 3}$ .
-Using the situation above, solve the following: $P\left(R \cup T^{\prime}\right)$ .

Question 19

A company has discovered a way of evaluating the success of both their radio and television advertising. If $R$ and $T$ are, respectively, the events that the radio advertising and television advertising are successful, $P(R)=0.62, P(T)=0.75$ , and $P(R \cap T)=\mathbf{0 . 4 3}$ .
-Using the situation above, state in words what probability is expressed by the following: $P\left(R^{\prime}\right)$

Question 20

A company has discovered a way of evaluating the success of both their radio and television advertising. If $R$ and $T$ are, respectively, the events that the radio advertising and television advertising are successful, $P(R)=0.62, P(T)=0.75$ , and $P(R \cap T)=\mathbf{0 . 4 3}$ .

-Using the situation above, state in words what probability is expressed by the following: $P(R \cup T)$ .

Question 21

A company has discovered a way of evaluating the success of both their radio and television advertising. If $R$ and $T$ are, respectively, the events that the radio advertising and television advertising are successful, $P(R)=0.62, P(T)=0.75$ , and $P(R \cap T)=\mathbf{0 . 4 3}$ .

-Using the situation above, state in words what probability is expressed by the following: $P\left(R \cap T^{\prime}\right)$ .

Question 22

A company has discovered a way of evaluating the success of both their radio and television advertising. If $R$ and $T$ are, respectively, the events that the radio advertising and television advertising are successful, $P(R)=0.62, P(T)=0.75$ , and $P(R \cap T)=\mathbf{0 . 4 3}$ .

-Using the situation above, state in words what probability is expressed by the following: $P\left(R \cup T^{\prime}\right)$ .

Question 23

A basketball coach plans to add two players from among five juniors and eight seniors. What is the probability that
-both people will be seniors?

Question 24

A basketball coach plans to add two players from among five juniors and eight seniors. What is the probability that
-the first will be a junior and the second will be a senior?

Question 25

A school has tabulated the favorite snacks of 1000 of its students in the two categories, males and females. Here are the results:
If one of the terms in the table above is selected at random, find each of the following probabilities.
-=\) _______

Question 26

A school has tabulated the favorite snacks of 1000 of its students in the two categories, males and females. Here are the results:
If one of the terms in the table above is selected at random, find each of the following probabilities.
- $P\left(I^{\prime}\right)=$ _______

Question 27

A school has tabulated the favorite snacks of 1000 of its students in the two categories, males and females. Here are the results:
If one of the terms in the table above is selected at random, find each of the following probabilities.
- $P\left(M^{\prime} \mid Z\right)=$ _______

Question 28

A school has tabulated the favorite snacks of 1000 of its students in the two categories, males and females. Here are the results:
If one of the terms in the table above is selected at random, find each of the following probabilities.
- $P(F \mid I)=$ _______

Question 29

A school has tabulated the favorite snacks of 1000 of its students in the two categories, males and females. Here are the results:
If one of the terms in the table above is selected at random, find each of the following probabilities.
- $P\left(Z \mid M^{\prime}\right)=$ _______

Question 30

A school has tabulated the favorite snacks of 1000 of its students in the two categories, males and females. Here are the results:
If one of the terms in the table above is selected at random, find each of the following probabilities.
- $P\left(F^{\prime} \mid Z^{\prime}\right)=$ _______

Question 31

A school has tabulated the favorite snacks of 1000 of its students in the two categories, males and females. Here are the results:
If one of the terms in the table above is selected at random, find each of the following probabilities.
- $P(F \cup Z)=$ _______

Question 32

A school has tabulated the favorite snacks of 1000 of its students in the two categories, males and females. Here are the results:
If one of the terms in the table above is selected at random, find each of the following probabilities.
- $P\left(M \cap I^{\prime}\right)=$ _______

Question 33

A school has tabulated the favorite snacks of 1000 of its students in the two categories, males and females. Here are the results:
If one of the terms in the table above is selected at random, find each of the following probabilities.
- $P\left(F \cap I^{\prime}\right)=$ _______

Question 34

A company estimates that the probability of a recession occurring in the next year is 0.4 . The company also estimates the probability that another company distributes a competing product in the next year is 0.5 . Finally, the company feels that the probability of both a recession occurring and a competing product being produced in the next year is $\mathbf{0 . 2 5}$ .
-In the situation above, if there is a recession, what is the probability that a company will distribute a competing product in the next year?

Question 35

A company estimates that the probability of a recession occurring in the next year is 0.4 . The company also estimates the probability that another company distributes a competing product in the next year is 0.5 . Finally, the company feels that the probability of both a recession occurring and a competing product being produced in the next year is $\mathbf{0 . 2 5}$ .
-In the situation above, if a company produces a competing product, find the probability that there will be a recession in the next year.

Question 36

A company estimates that the probability of a recession occurring in the next year is 0.4 . The company also estimates the probability that another company distributes a competing product in the next year is 0.5 . Finally, the company feels that the probability of both a recession occurring and a competing product being produced in the next year is $\mathbf{0 . 2 5}$ .
-In the situation above, find the probability that there will be either a recession or a competing product or both in the next year.

Question 37

A company estimates that the probability of a recession occurring in the next year is 0.4 . The company also estimates the probability that another company distributes a competing product in the next year is 0.5 . Finally, the company feels that the probability of both a recession occurring and a competing product being produced in the next year is $\mathbf{0 . 2 5}$ .

-In the situation above, let
$R=$ recession occurs during the next year and
$C=$ competing product is available in the next year.
Using an appropriate formula, determine whether the events $R$ and $C$ are independent.

Question 38

Given mutually exclusive events $C$ and $D$ for which $P(C)=0.61$ and $P(D)=0.34$ , find
- $P\left(D^{\prime}\right)$ .

Question 39

Given mutually exclusive events $C$ and $D$ for which $P(C)=0.61$ and $P(D)=0.34$ , find
- $P(C \cap D)$ .

Question 40

Given mutually exclusive events $C$ and $D$ for which $P(C)=0.61$ and $P(D)=0.34$ , find
- $P(C \cup D)$ .

Question 41

Given mutually exclusive events $C$ and $D$ for which $P(C)=0.61$ and $P(D)=0.34$ , find
- $P\left(C^{\prime} \cup D^{\prime}\right)$ .

Question 42

Given mutually exclusive events $C$ and $D$ for which $P(C)=0.61$ and $P(D)=0.34$ , find
- $P\left(C^{\prime} \cap D^{\prime}\right)$ .

Question 43

Two options an automobile buyer may purchase are air-conditioning $(C)$ and an automatic transmission $(T)$ . A dealer notes from his sales records that the probability of a buyer purchasing an automatic transmission is 0.60 and the probability that he purchased air-conditioning is 0.50 . The probability that the buyer bought air-conditioning if he bought an automatic transmission is 0.70 .
-In the situation above, find the probability that a buyer purchased both an automatic transmission and air-conditioning.

Question 44

Two options an automobile buyer may purchase are air-conditioning $(C)$ and an automatic transmission $(T)$ . A dealer notes from his sales records that the probability of a buyer purchasing an automatic transmission is 0.60 and the probability that he purchased air-conditioning is 0.50 . The probability that the buyer bought air-conditioning if he bought an automatic transmission is 0.70 .
-In the situation above, if a buyer purchased air-conditioning, find the probability that he bought an automatic transmission.

Question 45

Two options an automobile buyer may purchase are air-conditioning $(C)$ and an automatic transmission $(T)$ . A dealer notes from his sales records that the probability of a buyer purchasing an automatic transmission is 0.60 and the probability that he purchased air-conditioning is 0.50 . The probability that the buyer bought air-conditioning if he bought an automatic transmission is 0.70 .
-In the situation above, find the probability that a buyer purchased either air-conditioning or an automatic transmission.

Question 46

Two options an automobile buyer may purchase are air-conditioning $(C)$ and an automatic transmission $(T)$ . A dealer notes from his sales records that the probability of a buyer purchasing an automatic transmission is 0.60 and the probability that he purchased air-conditioning is 0.50 . The probability that the buyer bought air-conditioning if he bought an automatic transmission is 0.70 .
-In the situation above, find the probability that a buyer did not purchase either air-conditioning or an automatic transmission.

Question 47

Two options an automobile buyer may purchase are air-conditioning $(C)$ and an automatic transmission $(T)$ . A dealer notes from his sales records that the probability of a buyer purchasing an automatic transmission is 0.60 and the probability that he purchased air-conditioning is 0.50 . The probability that the buyer bought air-conditioning if he bought an automatic transmission is 0.70 .

-In the situation above, determine, using an appropriate formula, whether the events $C$ and $T$ are independent.

Question 48

Thirty percent of students attending a certain student mixer meet someone new to date. Forty percent of students attending the mixer dance at sometime during the mixer. Of those who dance, $60 \%$ meet someone new to date. A student who attends the mixer is randomly selected.
-In the situation above, find the probability that he/she either dances or meets someone new to date.

Question 49

Thirty percent of students attending a certain student mixer meet someone new to date. Forty percent of students attending the mixer dance at sometime during the mixer. Of those who dance, $60 \%$ meet someone new to date. A student who attends the mixer is randomly selected.
-In the situation above, find the probability that he/she has danced if you know that he/she met someone new to date.

Question 50

Thirty percent of students attending a certain student mixer meet someone new to date. Forty percent of students attending the mixer dance at sometime during the mixer. Of those who dance, $60 \%$ meet someone new to date. A student who attends the mixer is randomly selected.
-In the situation above, find the probability that he/she has neither danced nor met someone new to date.

Question 51

Thirty percent of students attending a certain student mixer meet someone new to date. Forty percent of students attending the mixer dance at sometime during the mixer. Of those who dance, $60 \%$ meet someone new to date. A student who attends the mixer is randomly selected.

-In the situation above, if $M$ is the event of meeting someone new and $D$ is the event of a student dancing, determine by calculation using a formula whether $M$ and $D$ are independent.

Question 52

Three families A, B, and C, are bidding on the same one -family house. The probabilities are $0.20,0.25$ , and 0.28 , respectively, that a given family eventually moves into the house.
-In the situation above, find the probability that either family A or C eventually moves into the house.

Question 53

Three families A, B, and C, are bidding on the same one -family house. The probabilities are $0.20,0.25$ , and 0.28 , respectively, that a given family eventually moves into the house.
-In the situation above, find the probability that none of the three families eventually moves into the house.

Question 54

Three families A, B, and C, are bidding on the same one -family house. The probabilities are $0.20,0.25$ , and 0.28 , respectively, that a given family eventually moves into the house.

-In the situation above, if $A$ is the event that family $A$ moves into the house, and $B$ is the event that family $B$ moves into the house, the events $\mathrm{A}$ and $\mathrm{B}$ are

A) independent.
B) mutually exclusive.
C) complementary.
D) none of these.

Question 55

A consumer has placed two orders for a new product from two different suppliers $X$ and $Y$ . The probabilities that the suppliers deliver the product on time are 0.40 for $X$ and 0.60 for $Y$ .45) If the probability of one supplier delivering the product on time has no effect on whether or not the other one does, find the probability that one or both of the suppliers will deliver the product in the required time.
-If the probability of one supplier delivering the product on time has no effect on whether or not the other one does, find the probability that one or both of the suppliers will deliver the product in the required time.

Question 56

A consumer has placed two orders for a new product from two different suppliers $X$ and $Y$ . The probabilities that the suppliers deliver the product on time are 0.40 for $X$ and 0.60 for $Y$ .45) If the probability of one supplier delivering the product on time has no effect on whether or not the other one does, find the probability that one or both of the suppliers will deliver the product in the required time.

-If $X$ is the event that supplier $X$ delivers the product on time, and $Y$ is the event that supplier $Y$ delivers on time, the events $X$ and $Y$ are:

A) independent.
B) mutually exclusive.
C) complementary.
D) none of these.

Question 57

The probability of $A$ given $B$ is expressed as $P(A \mid B)$ .

Question 58

If $P(A)=\frac{2}{5}$ and $P(B)=\frac{4}{5}$ , then $P(A \cup B)$ must be greater than 1 .

Question 59

Two events are independent if they cannot both occur at the same time.

Question 60

If $A$ and $B$ are two events, the probability that at least one of the two events occurs can be represented by $P(A \cup B)$ .

Question 61

The expressions $A \cup B$ and $(A \cap B)^{\prime}$ are equal.

Question 62

The expressions $A^{\prime} \cap B^{\prime}$ and $(A \cap B)^{\prime}$ are equal.

Question 63

To calculate the probability that both of two events will occur, we would most likely use the conditional formula.

Question 64

If the probability of an event $A$ is unaffected by the probability of an event $B$ , then the events $A$ and $B$ are mutually exclusive.

Question 65

The events of drawing a ten and a jack on a single draw of one card from an ordinary deck of 52 cards are independent events.

Question 66

If $A$ is the event of rolling a 3 on a roll of a die and $B$ is the event of rolling at least a 3 on the second roll of the die, then the events $A$ and $B$ are independent.

Question 67

If the probability that a company will make a profit or break even is $\frac{2}{7}$ , then the odds in favor of the company losing money are _______.

Question 68

If $A$ and $B$ are mutually exclusive events with $P(A)=0.15, P(B)=0.45$ , then $P\left\{(A \cup B)^{\prime}\right\}$ equals _______.

Question 69

If $A$ and $B$ are independent events with $P(A)=0.25, P(B)=0.30$ , then $P\left\{(A \cup B)^{\prime}\right\}$ equals _______.

Question 70

Given the sample space $S=\{1,2,3,4,5,6,7,8\}$ with $A=\{3,5,7\}, B=\{2,3,4,5,6\}$ , then $A^{\prime} \cap B=$ _______.

Question 71

If $C$ is the event that a student buys a stereo and $D$ is the event that the student buys a personal computer, then $P\left(C \cup D^{\prime}\right)$ can be described in words as the probability that _______.

Question 72

A vocational counselor believes that the probability that interest rates will go up is 0.40 . He further believes that the probability that a particular student will get a job at the end of the year if interest rates go up is 0.30 . Based on these estimates, the probability that both interest rates will go up and that the student will get the job is _______.

Question 73

If $A$ is the event that a product will be a financial success and $B$ is the event that production will be preceded by a marketing study, then the probability that the product will be a financial success if production will be preceded by a marketing study can be expressed symbolically as _______.

Question 74

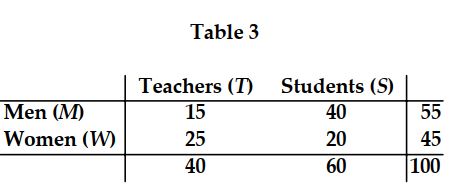
-Using Table 3, the probability that a person is both male and a teacher is _______.

Question 75

-Using Table 3, the probability that a person is a male given that the person is a student is _______.